С учетом уравнения (2.5.7) из (2.5.8) получим

N₂ = 2N₁cos45 (2.5.9)

3. Составим уравнение совместности перемещений. Из рис. 6б видно, что

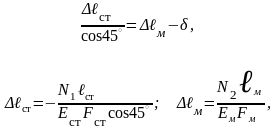
учитывая, что ℓ_ст = 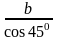, а ℓ_м = b, после подстановки получим

(2.5.10)

4. Решая совместно (2.5.9) и (2.5.10) получим:

Подставляя величины в Н и мм получим:

5. Напряжения в стержнях:

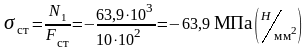
3. Геометрические характеристики сечений

1. Общие замечания

На прочность, жесткость и устойчивость стержней и стержневых систем большое влияние оказывают размеры и форма поперечного сечения стержней. Последние оцениваются геометрическими характеристиками сечений, к которым относятся: ширина b, высота h, площадь F сечения; положение центра тяжести х_с, у_с и главных центральных осей, статический момент S_у=FХ_c, осевые моменты инерции J_х и J_у центробежный момент инерции J_xy, полярный момент инерции J_ρ , радиусы инерции i_x и i_y, осевые W_x, W_y и полярный W_ρ моменты сопротивления, и другие характеристики.

Далее рассматриваются методические указания и пример расчета таких характеристик для сложного составного сечения из двух профилей.

3.2. Методические указания

1. Выписать из сортамента геометрические характеристики заданных стандартных профилей. Выполнить чертеж заданного плоского сечения в масштабе 1:1 или 1:2. На чертеже указать все необходимые размеры сечения.

2. Выбрать произвольные координатные оси х₁ и у₁, по отношению к которым определяется положение центра тяжести сечения. Удобно в качестве начальных вспомогательных осей принять главные центральные оси двутавра или швеллера.

3. Сложное сечение разбить на отдельные простые фигуры (швеллер-швеллер, швеллер-уголок, швеллер-двутавр, двутавр-уголок), площади и положение центров тяжести которых заранее известны и ранее выписаны.

4. Определить координаты центров тяжести простых фигур относительно начальных координатных осей х₁ и у₁ и нанести эти координаты на чертеже сечения.

5. Вычислить координаты центров тяжести всего сложного сечения по формулам:

(3.2.1)

(3.2.2)

Для плоских сечений, имеющих криволинейный контур, эти координаты вычисляются по формулам:

(3.2.3)

6. На чертеже плоского сечения нанести положение новых центральных осей х_с и у_с (проходящих через центр тяжести сложного сечения), проводя их параллельно осям х₁ и у₁.

Одновременно нанести координаты центров тяжести сечений каждой отдельной фигуры прокатного профиля относительно центральных осей х_с и у_с.

7. Найти значения осевых моментов инерции относительно центральных осей х_с и у_с, используя при этом формулы перехода к параллельным осям:

(3.2.4)

где Jх_i и Jу_i – моменты инерции отдельных фигур сложного сечения относительно собственных осей х_i и y_i, т.е. осей, проходящих через их центры тяжести, но проведенных параллельно осям х_с и у_с. Для прокатных профилей, входящих в состав сечения, величины Jх_i и Jу_i берутся из сортамента.

8. Найти величину центробежного момента инерции для заданного сложного сечения по формуле:

(3.2.5)

Значения Jх_iy_i – центробежных моментов инерции отдельных фигур сложного сечения относительно собственных главных центральных осей равны нулю.

Значения Jx_i y_i – центробежных моментов инерции равнобоких уголков, относительно собственных центральных осей определяются по формуле:

(3.2.6)

где  =  45;

J_max – максимальный момент инерции сечения уголка;

J_min – минимальный момент сечения уголка.

Jx_iy_i = 0, так как оси уголка х₀ и у₀ – главные. При определении центробежных моментов инерции сечений уголков, необходимо следить за знаком у центробежного момента инерции. Этот знак зависит от знака, входящего в формулы угла .

Если ось, относительно которой момент инерции уголка максимальный, проходит через вторую и четвертую четверти осей х_i и у_i, то  следует брать с плюсом. Если через первую и третью, то  следует брать с минусом.

9. Определить угол наклона главных центральных осей инерции сложного сечения к центральным осям х_с и у_с по формуле:

tg2₀ = 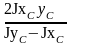(3.2.7)

10. Определить величину главных центральных моментов инерции по формуле:

(3.2.8)

11. При определении оси, относительно которой момент инерции будет максимальный, следует помнить, что поворот оси на угол ₀ увеличивает больший момент инерции относительно этой оси и уменьшает меньший.

12. Проверить правильность вычислений

(3.2.9)

13. Определить моменты сопротивления сложного сечения по формулам

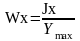(3.2.10)

(3.2.10а)

За расчетный момент сопротивления принимается больший.

14. Определить грузоподъемность Р и q по двум расчетным схемам из условия прочности по нормальным напряжениям

выразив соответственно М_max через Р, q, ℓ по 1 и 2 расчетной схеме.