
- •1. Общие методические указания
- •2. Осевое растяжение-сжатие
- •2.1. Общие положения
- •2.2. Методические указания к расчету статически определимых задач на примере кронштейна
- •2.3. Пример расчета кронштейна
- •2.3.1. Определение усилий в стержнях
- •2.3.2. Подбор сечений стержней
- •2.3.3. Определение напряжений в стержнях
- •2.3.4. Определение линейного перемещения узла
- •2.4. Методические указания к расчету статически неопределимых стержневых систем
- •2.5. Примеры расчета статически неопределимых стержневых систем
- •С учетом уравнения (2.5.7) из (2.5.8) получим
- •3. Геометрические характеристики сечений
- •Общие замечания
- •3.2. Методические указания
- •Пример расчета балки несимметричного сечения
- •4. Проверка прочности балки при плоском поперечном изгибе
- •4.1. Общие положения
- •4.2. Методические указания
- •4.3 Пример расчета
- •5. Расчет перемещений в балках при плоском поперечном изгибе
- •5.1. Общие пояснения
- •Методические указания
- •5.3. Пример расчета
- •Угол поворота на опоре а, θ(0), с учетом ординат на рис. 11 г будет:
- •6. Расчет статически неопределимой балки
- •6.1. Общие замечания
- •Методические указания
- •Определение лишних неизвестных по теореме о трех моментах
- •6.2.2. Определение «лишних» неизвестных способом сравнения перемещений
- •6.3. Пример расчета статически неопределимой балки
- •7. Сложное сопротивление
- •7.1. Общие замечания
- •7.2. Методические указания к расчету внецентренно нагруженных стержней
- •7.3. Пример расчета стержня на внецентренное сжатие
- •7.4. Методические указания к расчету вала
- •7.5. Пример расчета вала на изгиб с кручением
- •Задача 1.1. Расчет кронштейна
- •Исходные данные принимаются в соответствии с шифром студента, который необходимо получить у преподавателя. Численные данные к расчету кронштейна определяются по 1-й цифре шифра из следующей таблицы:
- •Численные данные к расчету статически неопределимой системы принимаются по 1-й цифре шифра из следующей таблицы:
- •Срок выполнения - 4 недели с момента выдачи
- •Исходные данные принимаются в соответствии с шифром студента, который необходимо получить у преподавателя. Численные данные к ргр-2 определяются по 1-й цифре шифра из следующей таблицы:
- •Исходные данные принимаются в соответствии с шифром студента, который необходимо получить у преподавателя. Численные данные к ргр-3 определяются по 1-й цифре шифра из следующей таблицы:
- •Исходные данные принимаются в соответствии с шифром студента, который необходимо получить у преподавателя. Численные данные к ргр-4 определяются по 1-й цифре шифра из следующей таблицы:
- •Исходные данные принимаются в соответствии с шифром студента, который необходимо получить у преподавателя. Численные данные к ргр-5 определяются по 1-й цифре шифра из следующей таблицы:
- •Задача 6.1. Расчет стержня на внецентренное сжатие
- •Исходные данные принимаются в соответствии с шифром студента, который необходимо получить у преподавателя. Численные данные к расчету определяются по 1-й цифре шифра из следующей таблицы:
- •Задача 6.2. Расчет вала на изгиб с кручением
- •Сопротивление материалов
- •198035,Санкт-Петербург, ул. Двинская, 5/7 Отпечатано в типографии фгоу впо спгувк,
- •198035, Санкт-Петербург, Межевой канал, 2.
2.5. Примеры расчета статически неопределимых стержневых систем
Пример 2.5.1.
Абсолютно жесткий брус закреплен с помощью шарнирно-неподвижной опоры и двух стальных стержней одинаковой длины ℓ и одинакового поперечного сечения F = 5 см2 (рис. 4а). Определить усилия и напряжения в стержнях от на грузки Р = 50 кН.
Решение.
1. Степень статической неопределимости системы: n = nр – nу = 4 – 3 = 1,
где
nр
= 4, так как имеют место реакции Rc,
Rd,
 и
и
 ;
;
nу = 3, т.к. для плоской системы в общем случае могут быть использованы 3 уравнения статики.
Система один раз статически неопределима.
2. Применяем метод сечений. Продольные усилия в стержнях АС и BD принимаем растягивающими и обозначим N1 и N2. Составим уравнение равновесия
ΣМ0 = 0, N1cos45°α + N2cos6002α – P · I,5α = 0 (2.5.1)
Можно составить еще два уравнения равновесия ΣХ = 0 и ΣY = 0, но в них войдут еще два неизвестных усилия - реакции в опоре О, которые нас не интересуют. Имеем одно уравнение с двумя неизвестными. Система один раз статически неопределима.
3. Для составления дополнительного уравнения перемещений рассмотрим деформацию системы. После нагружения системы силой Р брус ОАВ займет положение ОА1В1 (рис 46). Стержни удлиняются Δℓ1 = АА2 и Δℓ2 = ВВ2. Тогда из подобия треугольников ОАА1 и ОВВ1 получим
 =
=
 или
или
 =
=
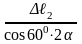
или
 =
=
 (2.5.2)
(2.5.2)
 =
=
 ;
;
 = N2
= N2
4. Решая совместно полученные уравнения равновесия (2.5.1) и перемещений (2.5.2), найдем N1 и N2:
N1
·
 +
+
 ·
·
 · 2 = 1,5 Р
· 2 = 1,5 Р
Тогда N1 = 0,707 Р · 50 = 35,35 кН,
N2 = P = 50 kH.
5. Напряжения в стержнях:
σ1
=
 =
=
 = 7,07 · 107
Па
= 70,7 МПа,
= 7,07 · 107
Па
= 70,7 МПа,
σ2
=
 =
=
 = 10 · 107
Па
= 100 МПа.
= 10 · 107
Па
= 100 МПа.
а)
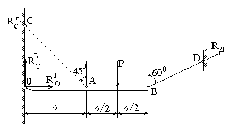
б)

Рис. 4
Пример 2.5.2.
Абсолютно жесткий брус подвешен на трех стальных стержнях одинаковой длины ℓ и одинакового поперечного сечения F = 4 см2 (рис. 5а). Определить усилия и напряжение, возникающие в стержнях от нагревания третьего стержня на 60°. Коэффициент линейного расширения αст = 12,5·10–6 1/град, Ест = 2 105 МПа.
Решение:
1. Степень статической неопределимости системы:
n = nр – nу = 3 – 2 = 1,
где nр = 3, число реакций;
nу = 2, число уравнений равновесия статики, которые могут быть использованы. В данном случае только два, все силы действующие на плоскую систему параллельны.
а) б)

Рис. 5
2. Предположим, что все стержни растянуты (рис. 5б). Составим уравнения равновесия:
У = 0, N1 + N2 + N3 = 0 (2.5.3)
MA = 0, N2а + N32а = 0, или N2 = 2N3 (2.5.4)
Система один раз статически неопределима, так как два уравнения равновесия содержат три неизвестные усилия.
3. Составим уравнение перемещений. После нагревания третьего стержня брус АВС займет новое положение А1В1С1. Тогда из подобия треугольников А1С1С2 и А1В1В2 получим зависимости:
 (2.5.5)
(2.5.5)
Изменение
длины третьего стержня произойдет в
результате его нагрева и возникающего
в нем усилия N3,
т.е.
 =
=
 Следовательно, у
Следовательно, у равнение
перемещений примет вид
равнение
перемещений примет вид
или αΔtEF + N3 – N1 = 2N2 –2N1 (2.5.6)
4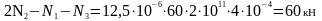 .
Решая совместно уравнения (1), (2) и (4),
найдем:
.
Решая совместно уравнения (1), (2) и (4),
найдем:

5 .
Напряжения в стержнях:
.
Напряжения в стержнях:

Пример 2.5.3.
В системе из трех стержней (рис. 6а) длина среднего стержня меньше проектной длины на = 1 мм. Наклонные стержни стальные с площадью Fст = 10 см2, вертикальный стержень медный с площадью Fм = 25 см2. Определить усилия и напряжения в стержнях после сборки конструкции. Ест = 2105 МПа; Ем = 1105 МПа; а = 1м; b = 1м.
Решение:
Степень статической неопределимости системы
 ,
,
где
 - число реакций
- число реакций
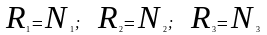
 –
число уравнений статики, которые могут
быть использованы
для решения системы.
–
число уравнений статики, которые могут
быть использованы
для решения системы.
Так как все силы сходятся в одной точке, то сумма моментов этих сил относительно любой точки системы тождественно равна 0
 а)
б)
а)
б)
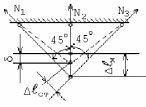
Рис. 6
В этом случае для плоской системы остается только два уравнения равновесия статики.
Схему системы после сборки (рис. 6б) рисуем, предполагая, что в действительности стержень испытывает сжатие.
2. Уравнения равновесия статики имеют вид:
Х = 0 –N1sin45 + N3sin45 = 0 N1 = N3 (2.5.7)
Y = 0 N1cos45+N2+N3cos45 = 0 (2.5.8)
