2.3.2. Подбор сечений стержней

Определим из условия прочности требуемую площадь сечения стального стержня

F_ст ≥ 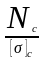= = 1,334 · 10^–3 м² = 13,34 см²

Поскольку стальной стержень состоит из двух прокатных уголков, то требуемая площадь сечения одного уголка

F_ст = = = 6,67 см²

По сортаменту подбираем стальной равнополочный уголок |_70х70х5, фактическая площадь сечения которого составляет f_с = 6,86 см². Следовательно, общая площадь подобранного по сортаменту сечения стержня из 2 |_ 70x70x5 мм фактически составит F_c = 2f_c = 2 · 6,86 = 13,72 см².

Определим из условия прочности требуемую площадь сечения деревянного стержня

F_дт = = = 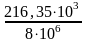27,044 · 10^–3 м² = 270,44см²

Вычислим требуемую сторону квадрата, образующего поперечное сечение деревянного стержня

h_дт ≥ = = 16,44 см

Поскольку деревянные брусья имеют размеры сечения в целых сантиметрах, то необходимо принять фактический размер h_д = 17 см, а фактическая площадь квадратного сечения бруса составит

F_д = h_д² = 17² = 289см²

2.3.3. Определение напряжений в стержнях

Напряжение в стальном стержне

σ = = = 87,52 МПа

Напряжение в деревянном брусе

σ = 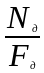= = – 7,49 МПа

2.3.4. Определение линейного перемещения узла

Предварительно вычислим продольные удлинения стержней кроншт­ей­на, учитывая фактически принятые площади сечений

Δℓ_c = = = 8,75 · 10^–4 м = 0,875 мм,

Δℓ_д = = = – 2,70 · 10^–3 м = – 2,7 мм,

Теперь построим план перемещения узла А (рис.3). Для этого в каче­стве полюса примем начальное положение узла А (точка А на плане перемещений). Соблюдая масштаб, отложим удлинение Δℓ_c и укоро­чение Δℓ_д из точки А параллельно соответствующим стержням; обо­значим концы этих отрезков буквами С и D. Поскольку в процессе деформирования кронштейна под нагрузкой Р, стержни не только уд­линяются и укорачиваются, но и должны повернуться ввиду сочлененности их в шарнирном узле, то необходимо далее через точки С и D провести перпендикуляры и отыскать точку их пересечения, кото­рую обозначим буквой А₁. Отрезок АА₁ плана перемещений является истинным линейным перемещением узла А кронштейна.

Для определения длины отрезка AA₁ проведем отрезки BD‌‌││АС и AE BD. Угол EAD равен α по заданной схеме кронштей­на. Углы BDA₁ и EAD равны между собой, так как образованы взаим­но перпендикулярными сторонами.

Найдем гипотенузу прямоугольного треугольника BDA₁:

А₁D = = =

Теперь найдем истинное линейное перемещение узла А как ги­потенузу прямоугольного треугольника ADA₁ по теореме Пифагора:

Δ_А = АА₁ = = =

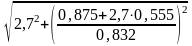= = 3,93 мм

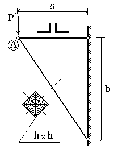
Рис.1 Рис.2

Рис.3

2.4. Методические указания к расчету статически неопределимых стержневых систем

Статически неопределимыми называются брусья и стержневые системы, внутренние усилия в которых нельзя определить с помощью одних уравнений равновесия. Поэтому при их расчете необходимо составлять дополнительные уравнения совместности перемещений, т.е. геометрические зависимости между удлинениями отдельных элементов системы, учитывающие характер деформации системы.

Число дополнительных уравнений, необходимых для расчета системы, характеризует степень ее статической неопределимости

n = n_p – n_y,

где n_p - число неизвестных реакций в системе;

n_y - число уравнений статики, которые могут быть использованы для нахождения реакций.

В элементах статически неопределимых систем усилия возникают не только от действия внешней нагрузки, а также и от других воздействий. Например, в результате изменения температуры, смещения опорных закреплений, неточности изготовления отдельных элементов конструкции. Изменение длин элементов системы выражается через усилия по закону Гука

Δℓ_i =

и подставляются в условия совместности перемещений.

Решая составленные уравнения равновесия и уравнения совместности перемещений, определяем продольные усилия во всех элементах системы. При определении температурных напряжений указанная схема расчета сохраняется. Составляем уравнения статики, необходимые для определения усилий в стержнях. Используя деформированное состояние системы при изменении температуры одного из стержней, составляем дополнительные уравнения совместности перемещений, а величины изменений длин нагретых или охлажденных элементов определяются алгебраическим суммированием приращений длин от усилий и от изменения температуры.

Суммирование деформаций должно быть согласовано с принятой деформационной схемой стержневой системы. Абсолютное удлинение от изменения температуры вычисляется по формуле

Δℓ_i = α_i · Δt_i · ℓ_i (2.4.1)

где α_i - средний коэффициент линейного расширения материала стержня;

Δt_i - изменение температуры;

ℓ_i - длина стержня.

Определение монтажных напряжений производится также из условий статики и условий совместности перемещений. В этом случае при составлении условий совместности перемещений учитывается наличие заданной неточности в длинах элементов системы. Так как фактические длины элементов, полученные при изготовлении, весьма мало отличаются от предусмотренных в проекте, то при определении абсолютных удлинений элементов по закону Гука берутся их проектные длины, а не фактические.

Общий порядок решения статически неопределимых стержневых систем следующий:

1) определяется степень статической неопределимости стержневой системы;

2) записываются и раскрываются уравнения равновесия, которые используются для решения задачи;

3) составляется схема перемещений системы, записывается необходимое число условий совместности перемещений, в которые подставляются перемещения стержней, зависящие от нормальной силы, возникающей в них. После преобразований условия совместности перемещений даны дополнительные уравнения, связывающие неизвестные нормальные силы в стержнях;

4) решается система уравнений, полученных в пунктах 2 и 3. Общее число уравнений равно числу неизвестных внутренних силовых факторов, которые и находятся после решения системы;

5) по известным нормальным силам находятся напряжения в каждом стержне.