6.2.2. Определение «лишних» неизвестных способом сравнения перемещений

При выборе основной системы за «лишние» неизвестные при расчете статически неопределимых балок способом сравнения перемещений принимаются опорные реакции и моменты в результате отбрасывания соответствующих «лишних» опорных связей.

Недостающие уравнения, так называемые уравнения совместности перемещений, число которых соответствует числу «лишних» неизвестных, составляются по условиям деформации.

Основным приемом раскрытия статической неопределимости балок является составление дополнительных уравнений совместности перемещений (прогибов и углов поворота) опорных сечений и приравниванием их к нулю, так как в заданной системе по направлению неизвестных опорных реакций и моментов наложены «лишние» связи. Решение этих дополнительных уравнений перемещений может быть выполнено различными способами: интегрирования дифференциального уравнения изогнутой оси методом начальных параметров, применением теоремы Кастильяно, интеграла Мора и способа Верещагина. Определив «лишние» неизвестные, из уравнений статики найти остальные реакции опор. Затем построить эпюры поперечной силы и изгибающего момента.

6.3. Пример расчета статически неопределимой балки

Для заданной статически неопределимой балки требуется:

Выяснить степень статической неопределимости балки (рис. 13а)

Определить «лишние» неизвестные двумя способами:

а) уравнением трех моментов;

б) способом сравнения перемещений.

Построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать по сортаменту двутавровое сечение, если =160МПа.

Определить эффективность (по расходу металла) статически неопределимой балки по сравнению со статически определимой, полученной определенным способом из заданной.

По эпюре изгибающих моментов изобразить форму изогнутой оси.

Применение теоремы о трех моментах.

Решение.

1. Основную систему для расчета неразрезной балки получим, если над всеми промежуточными опорами врежем шарниры, а в качестве «лишних» неизвестных примем изгибающие моменты в надопорных сечениях М_n. В данном примере балка дважды статически неопределима. Неизвестными являются опорные моменты М₁ и М₂ .

Опорный момент М₃ = -40 кНм, М₀ = 0 (рис. 13б). Расчетная схема балки с нумерацией опор и пролетов показана на рис. 13а.

2.. Эпюра изгибающих моментов в каждом пролете от внешней нагрузки представлена на рис. 13в. Момент на опоре 3 от силы Р₁ на конце консоли не считается нагрузкой, действующей в третьем пролете.

3. Составим уравнения трех моментов попарно для двух смежных пролетов слева направо:

Рис. 13

(6.3.1)

(6.3.2)

После сокращения уравнений (6.3.1) и (6.3.2) и, учитывая, что М₀ = 0 и М₃= –40 кНм, получаем:

20М₁+4М₂= 330

4М₁+18М₂= 665

Решив эти уравнения, найдем:

М₁= 9,535 кНм; М₂= 34,825 кНм

После определения моментов М₁ и М₂ задача стала статически определимой.

4 . Найдем опорные реакции. Для этого составим уравнения моментов и моментов всех сил поочередно слева или справа относительно опор неразрезной балки:

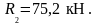
Проверка правильности вычисления реакций:

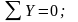R₀ + R₁ + R₂ + R₃ PP₁q = 0;

11,6 + 25,4 + 75,2 +71  40  20  20  5 = 0

00

Реакции определены правильно.

5. Построение эпюры поперечных сил Q (рис. 14)

Пролет 0–1:

Q = R₀ = 11,6 кН;

Пролет 1–2: Q = R₀ + R₁ = 11,6 + 25,4 = 13,8 кН

Q = R₀ + R₁ P = 11,6 + 25,4 – 40 = 26,2 кН;

Консоль: Q = +Р₁ = 20 кН

Пролет 2-3: Q = +P₁ R₃ + qz

При Z = 0 Q = +P₁  R₃ = 20  71 = 51 кН;

При Z = 5 Q = +P₁  R₃ + qz = 20  71 + 205 = 49 кН.

Определим координату Z, при которой изгибающий момент в пролете 3-2 будет экстремальным

Q = P₁  R₃ + qz = 0;

Рис. 14

6. Построение эпюры изгибающих моментов М (рис. 14б)

Пролет 0-1 0  z  M = R₀z;

Z	0	3
M	0	34,8

M=Rz+M;

Z	3	6
M	25,2	9,535

Пролет 1-2:

Z	2	4
M	18	35,0

Консоль: М=P₁ z

Z	0	2
M	0	40

Пролет 3-2: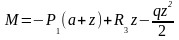

Z	0	5	2,55
M	40	35	25

7. Определение «лишних» неизвестных способом сравнения перемещений

Основная система показана на рис. 15а.

В качестве «лишних» неизвестных при решении примера способом сравнения перемещений примем реакции на опорах 0 и 3, т.е. R₀ и R₃. Составим уравнения перемещений (прогибов) опорных сечений 1 и 3 и приравняем их к нулю. Используем интеграл Мора, вычисленный по способу Верещагина. Для этого в основной системе в сечениях 1 и 3 прикладываем единичные силы Р₁=1. Строим эпюры изгибающих моментов в основной системе от действия внешних сил и моментов и от единичных сил Р₁ = 1 (рис. 15б).

8. Для определения реакций R₀ и R₃ составим выражения прогибов на опорах 0 и 3 и приравняем их к нулю

Рис. 15

Здесь  - площадь эпюры изгибающих моментов от заданных сил.

М⁰_с – ординаты эпюры изгибающих моментов от единичной Р_i нагрузки в сечениях 0 и 3 под центром тяжести площади _i и тогда 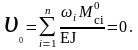Подставляя значения ω_i и , получим

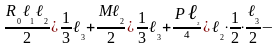
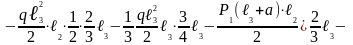
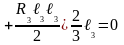
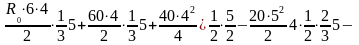
После сокращений уравнений получим

120R₀ + 20R₃  30 = 0

60R₀+ 225R₃  15287,5 = 0

Решив уравнение, найдем

R₀ = 11,6 кН; R₃ = 71,0 кН

9 . Для определения реакций R₁ и R₃ определяем изгибающий момент на опоре 2.

С оставим уравнения моментов относительно опорных сечений

или

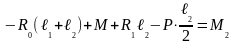
R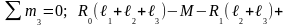 ₁ = 25,4 кН.

и ли

Таким образом, величины реакций при решении задачи обоими способами соответственно равны

10. Подбор сечения двутавровой неразрезной балки из условия прочности при изгибе

Тогда требуемый момент сопротивления

Принимаем двутавр № 22а , у которого W_х = 254 см³; площадь поперечного сечения F = 32,8 см².

Действительное нормальное напряжение

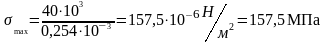
Расхождение в процентах

(недогрузка)

11. Исследование влияния лишних опор на прочность балки.

Образуем статически определимую балку из заданной статически неопределимой (рис. 16).

Определим реакции опор

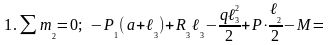0

или

кН;

или

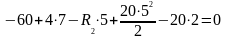
кН

86 + 74 – 40 – 20 – 20 · 5 = 0 0 ≡ 0. Реакция определена правильно.

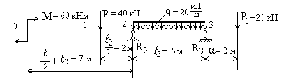
Рис. 16

Рис. 17

Построим эпюры Q и М.

Пролет 1–2:

Q = Р = 40 кН;

Пролет 2-3:Q = P +R2 qz;	Z	0	5
	M	46	54

Определим координату Z, при которой изгибающий момент в пролете 3–2 будет экстремальным

Q = P + R₂  qz = 0

Консоль: Q = P₁ = 20 кН;

Пролет 0–1 и 1–2:

М = М= 60 кНм;

М = М  Pz;	z	0	2
	M	60	20

Пролет 2–3:

М = М

Z	0	5	2,3
M	20	40	33

Консоль М = Рz

z	0	2
M	0	40

Эпюры Q и М показаны на рисунке 17.

Подбор сечения двутавровой статически определимой балки.

Требуемый момент сопротивления

Принимаем двутавр № 27, у которого W_x =3 71 см³; площадь поперечного сечения F = 40,2 см².

Перерасход материала составит

· 100 = · 100 = 22,5%

12. По эпюре изгибающих моментов на рис. 14в представлена форма изогнутой оси балки.