5. Задания для самостоятельного решения

1. Записать двойной интеграл в виде повторных интегралов двумя способами, если задана область D:

1. 

Ответ. .

2. 

Ответ. .

3. 

Ответ. .

4. 

Ответ. .

5. 

Ответ. .

6. 

Ответ. .

7. 

Ответ. .

8. 

Ответ.

2. Изменить порядок интегрирования в повторном интеграле:

1. .

Ответ. .

2. .

Ответ. .

3. .

Ответ. .

4. .

Ответ. .

3. Вычислить двойной интеграл:

1. 

Ответ. .

2. 

Ответ. .

3. 

Ответ. 4.

4. 

Ответ. -4.

4. Вычислить тройной интеграл от заданной функции по области (V), ограниченной указанными поверхностями:

1. 

Ответ. .

2. 

Ответ. .

3. 

Ответ. .

4. 

Ответ. 4.

5. 

Ответ. .

6. 

Ответ. 2.

7. 

Ответ. 8.

8. 

Ответ. 2.

9. 

Ответ. 1.

Ответ. 4.

11. 

Ответ. 1.

12. 

Ответ. 2.

Ответ. 3.

5. Вычислить с помощью тройного интеграла объем тела V, ограниченного поверхностями:

Ответ. .

Блок №2

1. Замена переменных в двойном интеграле

Пусть система уравнений

осуществляет взаимно-однозначное соответствие между областью (D) плоскости Оxy и областью (G) плоскости Оuv, пусть при этом функции x(u,v), y(u,v) непрерывно дифференцируемы и якобиан отличен от 0 во всех точках области G. Тогда имеет место формула замены переменных в двойном интеграле

Этой формулой пользуются в тех случаях, когда область (G) имеет более простую форму, чем (D). В частности, при переходе в полярную систему координат

J(u;v) = 

и

2. Замена переменных в тройном интеграле

Тройной интеграл иногда проще вычислить, если перейти к новой системе координат Оuvw. Если замена переменных происходит с помощью функций , , и эти функции осуществляют взаимно-однозначное соответствие между областью (Т) в системе Оxyz и областью (Т₁) в системе О₁uvw и якобиан непрерывен и не обращается в нуль, то справедлива формула

Н аиболее употребительными из криволинейных координат являются цилиндрические и сферические системы координат.

В цилиндрической системе координат каждой точке М пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел – длина вектора , где М – проекция точки М на плоскость 0xy,  – угол между вектором и положительным направлением оси Оx, z совпадает с третьей координатой точки М в декартовой прямоугольной системе координат (числа  и  являются полярными координатами точки М в системе Оxy). Переменные , , z могут принимать значения: 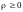, 0   <  (или –   < ), – < z < +. Уравнение  = с, где с – константа, с  0, задает цилиндр в пространстве, уравнение  = с задает полуплоскость, z = c – плоскость. Переход к цилиндрической системе координат осуществляется с помощью формул

Якобиан перехода равен J = . При этом

(Часто вместо z пишут просто z).

В сферической системе координат каждой точке М(x;y;z) пространства с заданной декартовой прямоугольной системой координат ставится в соответствие упорядоченная тройка чисел (, , ) – сферические координаты, где  – длина вектора  – угол между вектором и положительным направлением оси Оz, – угол между вектором и положительным направлением оси Оx (М, как и выше, – проекция точки М на плоскость Оxy). Переменные , ,  могут принимать следующие значения:   0, 0    , 0   < 2 (или –   < ).

Уравнение  = c, c  0 задает сферу радиуса c (чем и объясняется название системы координат), – однополостный круговой конус,  = c – полуплоскость. Формулы перехода к сферической системе координат имеют вид

Якобиан перехода J = ²sin. В новой системе координат