VI модуль Операционное исчисление Блок №1
1. Преобразование Лапласа и его свойства
Функцией-оригиналом
называется комплекснозначная функция
действительного аргумента
,
удовлетворяющая следующим условиям:
определена и является кусочно-гладкой на всей числовой оси;
при
;Существуют числа
и
,
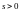такие что
;
точная
нижняя грань
таких s
называется порядком роста функции
.
Простейшим примером функции-оригинала является функция Хевисайда
Произведение
функций
и
обнуляет функцию
при
и не меняет ее значений при
:
Для
краткости всюду в дальнейшем будем
писать
вместо произведения
.
Если – функция-оригинал, то преобразование Лапласа, определяемое равенством
,
ставит
в соответствие функции
другую функцию
комплексного переменного
.
При этом
называют изображением функции
и пишут
или
.
Теорема
1. Если
– функция-оригинал с показателем роста
,
то функция
определена и является аналитической в
полуплоскости
.
Преобразование
Лапласа обладает следующими свойствами
(считаем
,
):
Свойство 1 (линейность).
.
Свойство 2 (подобие).
.
Свойство 3 (запаздывание оригинала).
.
Свойство 4 (смещение изображения).
.
Свойство 5 (дифференцирование оригинала).
где
.
Свойство 6 (дифференцирование изображения).
Свойство 7 (интегрирование оригинала).
.
Свойство 8 (интегрирование изображения).
,
где путь интегрирования соединяет точку p и бесконечно удаленную точку и целиком лежит в полуплоскости .
Имеет место следующая формула обращения преобразования Лапласа (формула Меллина): если , то
,
где
интеграл берется вдоль любой прямой
.
2. Таблица оригиналов и изображений
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения, теоремы и понятия.
По заданному оригиналу найти его изображение:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
.
Ответ.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
.
4. Задания для самостоятельного решения
По заданному оригиналу найти его изображение:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
.
Ответ.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
; 8)
;
9)
;
10)
;
11)
;
12)
.