ЗМІСТ

1 Розвязування ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ (ЛП) за допомогою ФУНКЦІй МНОЖЕННЯ МАТРИЦЬ в Excel 3

1.1 Формулювання задачі 3

1.2 Алгоритм розв’язування 4

1.2.1 Підготовка таблиці Excel для розв’язування задачі 4

1.2.2 Введення необхідних формул 6

1.2.3 Пошук оптимального рішення за допомогою симплекса-методу (перше симплекс-перетворення) 7

1.2.4 Друге симплекс-перетворення 10

2 Розв’язування задач оптимізації за допомогою програми “Поиск решения” в Excel 12

2.1 Розв’язування задачі лінійного програмування 12

2.1.1 Приклад задачі лінійного програмування про оптимальну структуру виробництва 12

2.1.2 Математичне формулювання задачі. Двоїста задача 12

2.1.2.1 Складання математичної моделі задачі про структуру виробництва (пряма задача) 12

2.1.2.2 Двоїста задача і задача про структуру виробництва 13

2.1.3 Введення імен для комірок і діапазонів комірок 14

2.1.4 Присвоєння імен коміркам і діапазонам комірок 16

2.1.5 Уведення формул в комірки 19

2.1.6 Представлення математичної моделі задачі ЛП за допомогою імен 22

2.1.7 Уведення даних про задачу ЛП у програму “Поиск решения” 23

2.1.8 Рішення задачі і вивід звітів 26

2.1.9 Аналіз оптимального рішення лінійного програмування на основі звітів 28

2.1.9.1 Структура "Отчета по результатам" 28

2.1.9.2 Структура "Отчета по устойчивости" 29

2.1.9.3 Структура "Отчета по пределам" 31

2.2 Розв’язування задачі цілочисельного програмування 32

2.2.1 Зміна умови задачі 32

2.2.2 Розв’язування задачі 33

2.3 Розв’язування задачі нелінійного програмування 34

2.3.1 Зміна умов задачі 35

2.3.2 Рішення задачі 35

3 ТРАНСПОРТНА ЗАДАЧА ЛП 38

3.1 Збалансовані та незбалансовані транспортні задачі ЛП 38

3.1.1 Загальні означення 38

3.1.2 Зведення незбалансованої задачі до збалансованої 39

3.1.3 Математична модель транспортної задачі ЛП 41

3.2 Розв’язування транспортної задачі за допомогою програми “Поиск решения” 42

3.2.1 Введення імен для комірок та діапазонів комірок 42

3.2.2 Уведення формул в комірки 44

3.2.3 Представлення математичної моделі транспортної задачі ЛП за допомогою імен 44

3.2.4 Введення даних у програму “Поиск решения”. Розв’язування транспортної задачі ЛП 44

4 Семестрове завдання 46

4.1 Вимоги до виконання та оформлення семестрового завдання 46

4.2 Варіанти семестрового завдання 47

5 Перелік основних питань для підготовки студентів до заліку 61

Література 63

1 Розвязування задач лінійного програмування (лп) за допомогою функцІй множення матриць в Excel

1.1 Формулювання задачі

Як приклад розглянемо наступну задачу.

Задача 1 Про оптимальну структуру виробництва

Фірма N збирає телевізори, відеомагнітофони і відеоплеєри і використовує при цьому комплектуючі вузли трьох типів: A, B, C. Норми використання вузлів на кожен виріб і їхні місячні запаси приведені в таблиці 1.1.

Таблиця 1.1

	Телевізори	Відео-магнітофони	Відєоплеєри	Наявність на складі
Тип A	2	2	1	800
Тип B	1	4	0	450
Тип C	2	1	1	600

Прибуток від продажу телевізорів, відеомагнітофонів і відеоплеєрів складає 75 у.о., 50 у.о. та 35 у.о. відповідно.

Потрібно знайти оптимальне рішення (пряма задача).

По побудованій симплекс таблиці виписати рішення двоїстої задачі.

Якщо х₁, х₂, х₃ – кількість телевізорів, відеомагнітофонів і відеоплеєрів, що випускаються, відповідно, то легко записати задачу ЛП (пряма задача):

Цільова функція:	Z = 75x1 + 50x2 + 35x3 → max.	(1)
Обмеження:	2x1 + 2x2 + x3 + t1 = 800, x1 + 4x2 + t2 = 450, 2x1 + x2 + x3 + t3 = 600.	(2)
Умова невід’ємності:	x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, t1≥ 0, t2 ≥ 0, t3 ≥ 0.	(3)

Зауваження Тут t₁, t₂, t₃ - додаткові перемінні.

Якщо відобразити через y₁, y₂, y₃ - двоїсті перемінні (тіньові ціни), то легко виписати двоїсту задачу:

Цільова функція:	Z’ = 800y1 + 450y2 + 600y3 → min.	(4)
Обмеження:	2y1 + y2 + 2y3 - u1=75, 2y1 + 4y2 + y3 – u2 = 50, y1 + + y3 - u3 = 35.	(5)
Умова невід’ємності:	y1 ≥ 0, y2 ≥ 0, y3 ≥ 0, u1≥ 0, u2 ≥ 0, u3 ≥ 0.	(6)

Зауваження Тут u₁, u₂, u₃ - додаткові двоїсті змінні чи нормовані вартості.

1.2 Алгоритм розв’язування

1.2.1 Підготовка таблиці Excel для розв’язування задачі

Запишемо вихідну симплекс-матрицю задачі (1)-(3).

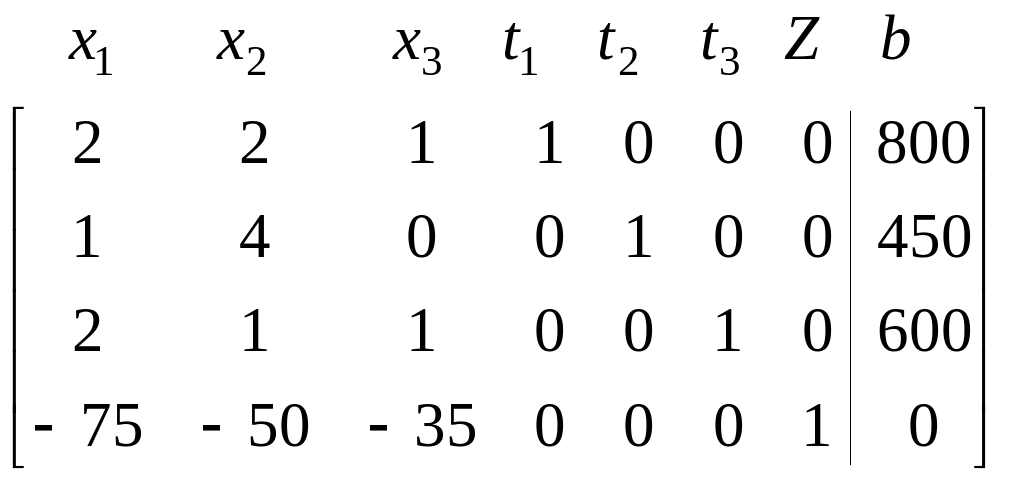
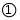(7)

1. Набираємо вихідну симплекс-матрицю в масиві (див. мал. 1.1)

М ал. 1.1

2. С творюємо вектори-стовпці: вектор , вектор_b , частки .

3. У творимо дві одиничні матриці: S и S’ .

4. Утворимо матрицю SA , такої ж розмірності, як і матриця .

5. С творимо масиви матриць - для збереження проміжних результатів (див. мал. 1.2 і мал. 1.3).

Мал. 1.2

Мал. 1.3

1 .2.2 Введення необхідних формул

1. Введемо в комірки одиничні значення (див. мал. 1.4)

М ал. 1.4

2. К омірки , що позначені як “вектор_b” дорівнюємо коміркам вектора b матриці , тобто

в комірці E7 уводимо формулу =I2

в комірці E8 уводимо формулу =I3

в комірці E9 уводимо формулу =I4

3. В комірки , що позначені як “частки” розміщуємо частки від ділення компонентів вектора на компоненти вектора , тобто

в комірку H7 уводимо формулу =E7/B7

в комірку H8 уводимо формулу =E8/B8

в комірку H9 уводимо формулу =E9/B9

4. М атрицю зробимо зворотною до матриці . Для цього здійснимо такі дії:

1) Виділимо матрицю (див. мал. 1.5)

Мал. 1.5

2 ) Вставка → Функция → МОБР.

3)У вікні, що з'явилося, указуємо масив матриці (див. мал. 6)

Мал. 1.6

4) Ctrl + Shift + Enter (одночасне натискання)

5. П омножимо матрицю зліва на матрицю і результат помістимо в масив . Для цього:

1) Виділяємо масив (див. мал. 1.7)

Мал. 1.7

2) Вставка → Функция → МУМНОЖ (див. мал. 1.8)

М ал. 1.8

3 )У вікні, що з'явилося, в поле вказуємо масив матриці , в поле - масив матриці .

4 ) Ctrl + Shift + Enter (одночасне натискання)

5) У масиві з'являється матриця (див. мал. 1.9)

Мал. 1.9