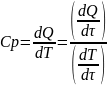2.8.3 Обработка и представление результатов измерений

Для обработки результатов работы следует открыть файл данных из электронной таблицы LibreOffice.Calc. В зависимости от модели процессора, операционной системы и настроек программы LibreOffice при этом может потребоваться указать кодировку UTF-8 или UTF-16 и стандарт столбцов «Английский-США». Полученные три столбца данных последовательно содержат следующую информацию: первый – температура эталонного образца в шкале Цельсия, второй – разность температур исследуемого образца и эталона, третий – время с начала эксперимента в минутах. Общее количество строк около 2000.

В первую очередь следует вычислить температуру исследуемого образца, складывая первый и второй столбцы, и построить график зависимости разности температур исследуемого и эталонного образца от температуры исследуемого образца. На нем должны уверенно выявляться один или два минимума, соответствующие плавлению эвтектического сплава (температуре линии солидус) и окончательному плавлению сплава заданного состава (температуре линии ликвидус). Оценив области нахождения этих минимумов, следует найти их точные значения, используя функцию MIN().

При оценке теплового эффекта следует иметь в виду следующие моменты. Если на два образца одинакового размера поступает тепловой поток одинаковой интенсивности, то разница в скоростях их нагрева будет определяться разницей теплоемкостей. Образец, имеющий более высокую теплоемкость, будет нагреваться медленнее. Однако, эта разница не может постоянно увеличиваться, поскольку образцы тоже обмениваются теплом. В результате тепловой поток на менее нагретый образец окажется выше, чем на соседний и разница температур стабилизируется на некотором значении, если теплоемкости образцов не будут меняться с температурой. Иначе разница температур будет меняться по мере нагрева, что и наблюдается в опытах.

Если в материале образца происходит превращение, сопровождающееся тепловым эффектом, то ход температурной зависимости еще усложняется. На следующем рисунке представлена идеализированная (модельная) зависимость разности температур исследуемого образца и эталона, если в исследуемом образце происходит эндотермическое превращение.

Рисунок 8.2. Возможный вид зависимости разности температур исследуемого и эталонного образцов от времени в отсутствие процессов, сопровождаемых тепловым эффектом (синяя кривая), и при протекании в интервале времени от 60 до 90 мин процесса, сопровождающегося поглощением тепла, например, плавления образца (красная кривая). Черные линии поясняют алгоритм вычисления теплового эффекта интегрированием зависимости.

Красная кривая между точками 1 и 2 характеризует скорость процесса плавления. Действительно, в соответствии с определением теплоемкость образца равна производной теплоты (Q) по температуре. Если продифференцировать числитель и знаменатель по времени, то получим отношение производной количества тепла по времени к производной температуры по времени:

(22.7)

Применяя это уравнение к описанию хода температурной зависимости от времени, учтем, что производная количества тепла по времени (тепловой поток) в этом случае определяется произведением теплоты плавления (H) на скорость процесса плавления (v). Можно показать. что производная температуры по времени при постоянной скорости нагрева эталона приближенно пропорциональна разности температур образца и эталона:

(22.8)

В этом выражении K_U – постоянная установки, зависящая от площади поверхности образца, конфигурации нагревателя и еще ряда характеристик, а t* - разность температур образца и эталона за вычетом той части, которая обусловлена различием их теплоемкостей. Если интерес представляет только качественный характер зависимости скорости процесса от времени, то значение множителя можно не вычислять, оценивая скорость в условных единицах.

Для ее вычисления следует из значений разности температур, находящихся на прямой, соединяющей точки 1 и 2 на рисунке 1 вычесть экспериментальные значения, находящиеся на кривой, выделенной красным цветом. Аналитически в электронных таблицах это выполняется чрезвычайно просто. Действительно, если первая точка имеет координаты ₁ и t₁, а вторая ₂ и t₂, то уравнение прямой линии между этими точками имеет вид:

(22.8)

Поэтому искомые значения следует вычислять по формуле:

(22.8)

размещая результаты во всех ячейках в интервале времени между точками 1 и 2. Если теперь по этим данным построить график, то получающаяся зависимость может иметь вид, представленный на рисунке 2.

Рисунок 8.3. Возможный вид зависимости скорости процесса плавления от времени.

Реальная кривая может иметь значительно более сложный вид, на основании которого можно сделать интересные выводы.

Порядок обработки результатов

1. По завершению работы программы Thermoscan-standard определить значение теплового эффекта на участке протекания процесса и записать полученные значения.

2. Извлечь результаты измерений из файла данных в электронные таблицы.

3. Вычислить температуру исследуемого образца.

4. Построить на отдельном листе график зависимости разности температур исследуемого образца и эталона от температуры исследуемого образца.

5. Вычислить значения разности температур образца и эталона, обусловленные только протеканием процесса.

6. Построить на отдельном листе график зависимости величины, пропорциональной скорости от времени, проанализировать его и сделать выводы.

7. Определить характерные температуры (линий солидус, ликвидус или обеих) для сплава заданного состава.

Зачетные результаты:

1. В книге электронных таблиц, представленной на проверку, на первой странице с названием «Результаты» должна быть представлена следующая информация:

   1. В ячейке «А1» – значение температурной остановки (среднее для наклонной площадки), в ячейке «В1» – единицы измерения;

   2. В ячейке «А2» – масса образца до опыта, в ячейке «В2» – единицы измерения;

   3. В ячейке «А3» – масса образца после опыта, в ячейке «В3» – единицы измерения;

   4. В ячейке «А4» – степень диссоциации исследованного образца;

   5. В ячейке «А5» – скорость процесса диссоциации, в ячейке «В3» – единицы измерения;

   6. Начиная с ячейки «А7» должны быть четко сформулированы выводы по работе.

В ячейках А1–А5 должны быть ссылки на ячейки на других листах книги электронных таблиц, на которых выполнены вычисления по известным формулам с получением представленного результата, а не сами числовые значения!

2. Правильно оформленный график зависимости разности температур исследуемого образца и эталона от температуры исследуемого образца на отдельном листе электронных таблиц со всеми необходимыми подписями и обозначениями.