Изображение изохорного тп на тs–диаграмме

Соответственно, количество тепла на ТS–диаграмме изохорного ТП определяется площадью под изохорой 1-2, то есть S_1-2-3-4-1 .

Долю поступающего (отводимого) в рабочее тело тепла, затраченного на изменение внутренней энергии Du, определим, принимая во внимание 1-й закон термодинамики:

. (7.2.10)

Следовательно, доля тепла на совершение работы деформирования будет:

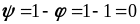. (7.2.11)

Изотермический процесс

Изотермический процесс, характеризующийся условиями T = const и dT = 0, может протекать, например, в цилиндре поршневого двигателя, в котором по мере подвода (отвода) тепла к газообразному рабочему телу поршень двигателя перемещается по такому закону, при котором объём рабочего тела увеличивается (уменьшается) настолько, что его Т остаётся неизменной.

В этом случае из уравнения Клапейрона получаем:

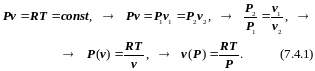
Из (7.4.1) видно, что объём рабочего тела при T = const изменяется обратно пропорционально его Р (закон Бойля-Мариотта). Графиком процесса является изотерма (изотерма (греч.) – линия одинаковой температуры; изо – равный, одинаковый, терм – тепло), представляющая собой на Рv-диаграмме равнобокую гиперболу, для которой координатные оси Р и v служат асимптотами (см. рис. 7.4.1).

И зображение изотермического процесса на Pv-диаграмме

На графике процесс 1-2 является прямым и обеспечивается поступлением тепла в рабочее тело. Процесс же 1-3 является обратным. В этом случае рабочее тело отдаёт тепло в ОС.

Работа деформирования газообразного рабочего тела в изотермическом процессе 1-2 будет:

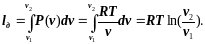(7.4.2)

Принимая во внимание (7.4.1), формулу (7.4.2) можно представить в следующих видах:

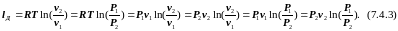
На Рv-диаграмме l_д в процессе 1-2 соответствует площади S_1-2-4-5-1.

Располагаемая работа в изотермическом процессе 1-2 определяется как

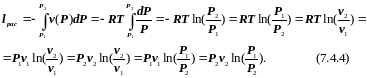
Сравнивая (7.4.3) и (7.4.4), видим, что в изотермическом процессе располагаемая работа равна работе деформирования рабочего тела, то есть в этом процессе вся работа деформирования превращается в полезную работу. Этот факт предопределил применение изотермы в цикле Карно, который является циклом идеальной тепловой машины. Соответственно, на Рv-диаграмме l_рас в процессе 1-2 соответствует площади S_1-2-6-7-1.

Применительно к изотермическому процессу уравнение (5.3.7) имеет вид du = C_V,удdT = 0. Нулю также равняется и изменение энтальпии рабочего тела в этом процессе di = C_P,удdT= 0. Принимая во внимание первый вид дифференциального уравнения 1-го закона термодинамики, получаем:

dq_Т = du + dl_д = 0 + dl_Д = dl_д.

Из данного выражения видно, что в изотермическом процессе всё подводимое (отводимое) к рабочему телу тепло затрачивается на совершение работы его деформирования.

Полученная взаимосвязь между dq_Т и dl_Д позволяет определить изменение энтропии в изотермическом процессе:

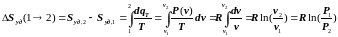.(7.4.5)

Аналогичный результат получается и при использовании для вычисления DS_уд(12) формулы (6.4.3), так как при изотермическом процессе :

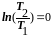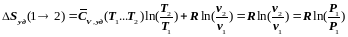
В связи с тем, что в изотермическом процессе теплоёмкость вещества равна бесконечности (см. 4.1), то определить количество тепла, подведённого (отведённого) к рабочему телу в этом процессе при помощи теплоёмкости, нельзя. Это можно сделать только через изменение энтропии в этом процессе. Используя уравнение (6.2.10) и учитывая (7.4.5), получаем:

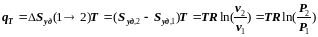. (7.4.6)