Решение с помощью дискриминанта

Пример 1. x³-3x²+3x-1=0

Решение:

a=1, b=-3, c=3, d=-1

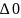=b² - 3ac => = (-3)²-3×1×3 => =9-9=0

=2b³ - 9abc+27a²d => =2×(-3)³-9×1×(-3)×3+27×1²×1 => =-54+81-27 => =0

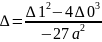=> (0)² =

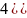
С= => 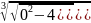=> 0=C

, где u = (-1 + ), а n равно либо 1, либо 2, либо 3.

Если подставить в эту формулу соответствующие значения величин, вы получите

возможные решения данного вам кубического уравнения. Подставьте их в

исходное уравнение и если равенство соблюдено, то решения правильные.

Например, если, подставив значения в формулу, вы получили 1, подставьте 1

в x³ - 3x² + 3x - 1 и получите 0. То есть равенство соблюдено, и 1 является одним из решений данного вам кубического уравнения.

Замена переменной

Пример 1. Найти действительные корни уравнения x³ + 12x² + 3x + 4 = 0.

Можно решать несколько иначе.

Решение:

Для данного уравнения a = 1, b = 12, c = 3, d = 4.

Сделаем замену переменной x = y - = y- = y-4

(y - 4)³ + 12(y - 4)² + 3(y - 4) + 4 = 0<=>

<=> y³ - 12y² + 48y - 64 + 12y² - 96y + 192 + 3y - 8 = 0 <=> y³ - 45y + 120 = 0.

Следовательно, p = -45, q = 120, Δ = (60)² - (15)³ = 225 >0. Значит, исходное уравнение имеет один действительный корень.

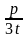Теперь сделаем следующую замену переменной y = t - = t+ = t+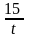 Получим

Это уравнение домножим на t³ и получим квадратное уравнение относительно t³

t⁶ + 120t³ + 3375 = 0

Получаем

Теперь можно найти y по формуле y = t +

Вместо t можно подставить или результат будет одинаковый.

1)

2)

Действительный корень исходного уравнения равен

О твет:

Используемые источники:

• http://edu.sernam.ru/book_el_math.php?id=63

• https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9A%D0%B0%D1%80%D0%B4%D0%B0%D0%BD%D0%BE

• https://www.tutoronline.ru/blog/uravnenija-vysshih-stepenej

• http://1cov-edu.ru/mat_analiz/funktsii/ratsionalnye/mnogochleny/kubicheskie-uravneniya/formula-kardano

• http://festival.1september.ru/articles/578572/

• И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009. Г. Корн, Справочник по математике для научных работников и инженеров, 2012.