Муниципальное автономное общеобразовательное учреждение
«Лицей №29»
кафедра математики, информатики и естественных дисциплин
Уравнения третьей степени
и их решения.
Формула Кардано
Выполнил: ученик 11 класса «Г»
Васильченко Сергей Владимирович
Научный руководитель: учитель математики
Топчий Елена Александровна
Тамбов
2017
Содержание:
Историческая справка
Научная справка
Решение уравнений с использованием формулы для решения квадратного уравнения
Формула Кардано
Таблица Горнера
Решение с помощью дискриминанта
Замена переменной
Используемые источники
Историческая справка
В конце 1534 года гениальный венецианский математик и ученный Никколо Тарталья за несколько дней до математического состязания находит способ решения «неполных» кубических уравнений, благодаря которой выигрывает на этом соревновании.
К 1539 Кардано заканчивает свою первую книгу, целиком посвященную математике «Практика общей арифметики». В январе этого же года Кардано обращается к Тарталье с просьбой передать ему правила решения этих уравнений, на что получил отказ. Лишь через почти полгода Тарталья дает себе уговорить и открывает секрет Кардано.
К 1543 году Кардано научился решать с помощью формулы, которой пользуются и сегодня, не только «неполные» кубические уравнения, но и «полные», т. е. содержащие элемент x2.
Научная справка
Формула Кардано.
Для уравнения х3 + рх + q = 0
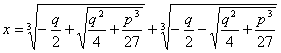
Выражение D = –4p3 – 27q2 называется дискриминантом уравнения.
При D < 0 уравнение имеет один действительный корень и два комплексных, сопряжённых между собой.
При D = 0 все три корня действительны, причём, по крайней мере, два из них равны.
При D > 0 уравнение имеет три различных действительных корня. Формула Кардано даёт один из них, скажем, х1, а два других даёт квадратное уравнение, полученное приравниванием нулю квадратного трёхчлена – частного от деления левой части на двучлен-разность.
Таблица Горнера
an-1
an
…
a2
a1
a0
…
c
bn-1=cbn-2+an-1
r(x)=f(c)=cbn-1+an
b2=cb1+a2
b1=cb1+a1
b0=a0
Формула Виета для кубического уравнения
Дискриминант кубического уравнения
Вычислим Δ0 = b2 - 3ac
Вычислим Δ1= 2b3 - 9abc + 27a2d
Затем вычислим Δ = (Δ12 - 4Δ03) ÷ -27a2
У кубического уравнения, если дискриминант положительный, то уравнение имеет три решения; если дискриминант равен нулю, то уравнение имеет одно или два решения; если дискриминант отрицательный, то уравнение имеет только одно решение. Кубическое уравнение всегда имеет по крайней мере одно решение, потому что график такого уравнения пересекает ось X по крайней мере в одной точке.
Вычислите
С=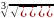
.
Эта величина позволит вам найти корни
кубического уравнения.
Корни
(решения) кубического уравнения
вычисляются по формуле
где n равно либо 1, либо 2, либо 3.
Решение уравнений при помощи формулы для решения квадратного уравнения (уравнения без свободного члена)
Пример 1. x3+3x2-4x=0
Решение:
x(x2+3x-4)=0
Осталось найти корни квадратного трёхчлена
x2+3x-4=0
D = 32-4×(-4)=9+16=25=52
x1,2=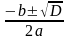
=
=
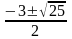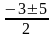=> x1=-4;
x2=1
Ответ: 0;1;-4
Пример 2. - 6x3-5x2 - x=0
Решение:
x(-6x2-5x-1)=0
Осталось найти корни квадратного трёхчлена
-6x2-5x-1=0 => 6x2+ 5x+1=0
D=52-4×6×1=25-24=1
x1,2=
=
=
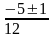=> x1=
-
;
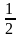x2=
-
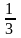
Ответ: 0; - ; -
Пример
3.
=
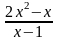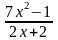
Решение:
= => (2x2-x)(2x+2)=(x-1)(7x2-x) => 4x3+4x2-2x2-2x=7x3-x2-7x2+x =>
=> x3(4-7)+x2(4-2+1+7)-x(2+1)=0 => -3x3+10x2-3x=0 => 3x3-10x2+3x=0
x(3x2-10x+3)=0
Осталось найти корни квадратного трёхчлена
3x2 - 10x+3=0
D1= (-5)2 - 3×3 = 25-9 = 16 = 42
x1,2=
=
=> x1=3;
x2=
Ответ: 0; 3; .