§6.1 Принцип Гюйгенса-Френеля (6.1.1.). Метод зон Френеля (6.1.2.)

6.1.1.

Полагается, что:

1. Все точки волнового фронта являются источником вторичных волн.

2. Все элементарные источники когерентны, втор. волн интерферируют между собой.

Френель дал выражение для результирующей волны в каждой точке волнового поля:

( ,t) = 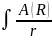·f(α)· ·dS.

Смысл параметров и функциональных зависимостей величин входящих в интеграл ясен из поясняющего рисунка.

6.1.2. Метод зон Френеля

Сферический волновой фронт Френель предложил разбивать на кольцевые зоны, обеспечивая разность хода (т.е. сдвиг по фазе на ).

Приближённо можно с читать

А = А₁ - А₂ + А₃ – А₄ +…. А_N

Поскольку для любого А_m = (А_m-1 + А_m+1) соответственно имеем, используя чётные m :

А = (А₁ - А_N) для чётного числа зон N

и А = (А₁ + А_N) для нечётного N.

При N 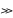1 в точке М наблюдения дифракционной картины

А = А₁ и I = 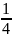I₁.

Удивительный результат: при открытой только первой зоне имеем – I₁ = 4I₀ .

Заметим, что разбивая саму зону Френеля на подзоны и используя диаграмму сложения амплитуд, развёрнутых на одинаковый угол (фазовый сдвиг), можно находить результирующую амплитуду в данной точке дифракционной картины.

§ 6.2 Дифракция Фраунгофера.

Рассмотрение соответствует плоскому фронту – “дальней зоне”

6.2.1. Дифракция на одной щели

Считаем волну, падающую на узкую щель (с шириной а λ) плоской. Щель разбивают на продольные зоны так, что фазовый сдвиг лучей идущих от их краёв в данном направлении ( под ∠ θ) равнялся .

Для наблюдения:

максимумов интенсивности а sin θ = (2m +1) (6.1)

минимумов - а sin θ = m λ, (6.2) где m = 1, 2, 3..

Угловая ширина центрального максимума δ = , других- . Их число задаётся условием: sin θ =1  m_max = .

Аналитический расчёт амплитуды волнового поля, основанный на учёте вклада элементарных зон щели при наличии фазового сдвига колебаний, даёт для интенсивности в точке наблюдения

I_θ = I₀ 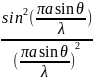, (6.3)

Где I₀ – интенсивность в центре экрана наблюдения дифракционной картины.

1. Для θ = 0 из (6.1) с учётом,что 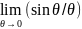→ 0, следует:

A (0) = A₀ ; I(0) = I₀

2. Положение побочных максимумов задаётся условием:

sin = 1 или = (2m+1)

Их величина I_{m, поб.} = I₀ /[ (2m+1)² ]

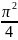3. Минимумы следуют из условия:

sin = 0

6.2.2. Дифракционная решётка

При наличии большого числа параллельных периодически расположенных щелей интенсивность в точках экрана определяется выражением:

I_θ = I₀ · (6.4)

Видно, что итоговая интенсивность многолучевой интерференции модулируется фактором, обусловленным действием одной щели.

Чем меньше отношение . тем плавнее ход огибающей.

Рисунок иллюстрирует угловую зависимость I (θ).

Важнейшие черты такой картины следующие:

а) Положения главных максимумов как и в многолучевой интерференции

d sin θ = m λ ( m = 0,1, 2, 3, … ) (6.5)

Интенсивность в главных максимумах в N² раз больше таковой в случае одной щели;

б) Главные максимумы (первого порядка) расположены между минимумами ограничивающими центральный максимум при дифракции на одной щели; их общее число М = 2m +1, где m= .

Угловая ширина главных максимумов =

Дополнительные максимумы числом N -2 расположены между главными максимумами.

в) Главные минимумы расположены под углами удовлетворяющих условию а sin θ = m λ

Дополнительные минимумы определяются соотношением

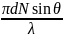= πm* (m*= 1, 2, … N-1, N +1, N +2… 2N -1, 2N+1… )

Дисперсия и разрешающая сила решётки

Угловой дисперсией спектрального прибора называют величину

D = = 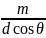(6.6)

Она определяет угловую ширину спектра.

Линейная дисперсия D = F 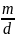, где F - фокусное расстояние линзы.

Разрешающая способность R

Понятие связано с задачей разрешения (опознавания,разделения) двух близко лежащих линий.

Согласно Рэлею R = =mN, (6.7)

где m - порядок спектра, N - число штрихов решётки. Число N может равняться 10³.