
- •§ 1.1 Гармонические периодические волны
- •§ 1.2 Волновое уравнение для плоских волн
- •§ 1.3 Принцип суперпозиции (1.3.1) и спектр колебаний (1.3.2)
- •§ 2.1 Цепочка атомов и волновое уравнение для непрерывной среды
- •§ 2.2 Энергия упругих волн
- •§ 3.1 Волновое уравнение для эл.-м.Волн
- •§ 2.2 Характеристики эл.-м. Волны
- •§ 2.3 Энергия эл.-м. Волны
- •§2.4 Импульс эл.-м. Волны. Световое давление.
- •§ 4.1 Волновые пакеты (4.1.1). Бигармоническая волна (4.1.2)
- •§ 4.2 Групповая скорость. Соотношения Рэлея
- •§ 4.3 Соотношение неопределённости для волн
- •§ 4.4 Круговая и эллиптическая поляризация как результат
- •§ 5.1 Интерференция от двух источников
- •§ 5.2 Стоячие волны
- •§ 5.3 Положения геометрической и волновой оптики
- •§6.1 Принцип Гюйгенса-Френеля (6.1.1.). Метод зон Френеля (6.1.2.)
- •§ 6.2 Дифракция Фраунгофера.
- •§ 6.2 Дифракция Френеля
§ 5.3 Положения геометрической и волновой оптики
5.3.1. Некоторые понятия
Оптикой называют раздел физики, в котором изучаются закономерности излучения, распространения и взаимодействия света с веществом.
В геометрической оптике пренебрегают волновой природой света и рассматривают его как совокупность лучей, подчиняющихся определённым закономерностям.
Классическая волновая оптика исходит из линейности сред распространения света (ε и μ полагают не зависящими от напряжённости эл. поля световой волны).
И наоборот, нелинейная оптика (сложилась сравнительно недавно) исходит из наличия таких зависимостей. Нелинейные эффекты проявляются при высоких интенсивностях (лазерные источники) излучения.
В
изотропных средах в большинстве случаев
μ
 .
.
Абсолютным показателем преломления среды является
n
= =
=

Длины
волн в вакууме λ0
и среде λ
связаны соотношением:
 = n.
= n.
5.3.2. Интерференция в практически параллельных лучах
Иначе
в “дальней
зоне”
(λ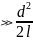 ).
).
Случай двух синфазных излучателей
(например, точечных источников или параллельных узких щелей – Юнга).
Геометрическая разность хода r = r2 - r1 = d sin θ
Оптическая разность хода rопт. = n( r2 - r1) = n r = n d sin θ
Максимум интенсивности при условии rопт. = m λ, m = 0, 1, , 2, , 3…
или
при фазовом сдвиге
 =
n
d
sin
θ
=
n
d
sin
θ
Максимумы
расположены симметрично относительно
прямой, направленной к источникам и
 линии
их расположения.
линии
их расположения.
Соответственно минимумы интенсивности интерференционной картины
возникают
при условии
 или
rопт.
=(2m
+
1)
.
или
rопт.
=(2m
+
1)
.
Для угловой и линейной ширины максимумов имеем:
Для
максимума нулевого порядка
θ0
= 2│
θmin│=
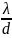 ,
,
0
=
 .
.
Для
максимумов первого и последующих
порядков она практически не меняется
вплоть до углов наблюдения приближающихся
к
. Число максимумов (соответственно и
минимумов) ограничено: m

Таким образом, при интерференции световой поток перераспределяется – формируются “пучки” излучения под определёнными углами.
Интерференция от двух одинаковых источников
Из выражения (5.1) для квадрата амплитуды результирующего колебания в интерференционной картине имеем:
I(θ)
= 2I(1
+ cos
 )
= 4I
cos2
)
= 4I
cos2

При отсутствии начального фазового сдвига у источников
= d sin θ
Более того:
2I(1
+ cos
)
= 4I
cos2
= 4I
cos2

I(θ)
=
 (5.2)
( для
N
=2)
(5.2)
( для
N
=2)
5.3.3. Многолучевая интерференция
Если число источников N, тогда этот параметр входит в числитель последнего (5.2) выражения в значение аргумента
I(θ)=
I0
|
К выражению (5.2.а) можно прийти путём вычисления амплитуды результирующего колебания в точке, где сходятся N одинаковых лучей , фаза каждого из которых отличается фазы предыдущего на постоянную величину φ.
Складывая векторы амплитуд (метод диаграмм), для многоугольника. вписанного в окружность, можем записать:
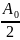 =
R
sin
и
=
R
sin
и
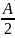 = R
sin
= R
sin
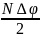
Исключив R для результирующей амплитуды A получаем:
A
=A0

Откуда вытекает выражение (5.2.а). Следствием является:
I = N 2 I0
при разности фаз φ = 2πm или разности хода rопт. = m λ, где m – порядок глвного максимума.
В промежутке между главными максимумами располагаются N-1 минимумов с нулевой интенсивностью (числитель равен нулю при
=
m*
π,
m*
=
1,
2, 3,
...N-1
или
φ
=
 2π).
2π).
С увеличинием числа N итерфер. лучей главные максимумы сужаются.
Вторичные максимумы, отделяющие минимумы, слабы на фоне главных максимумов. Угловая и линейная ширина последних в N раз меньше, чем в случае двух излучателей
φ+1,-1
=
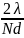 ,
=
,
=

Гл. 6 ДИФРАКЦИЯ СВЕТА
Под Д. понимают попадание света в область геометрической тени в среде с резкими неоднородностями. Это совокупность явлений, обусловленных перераспределением энергии волнового поля.

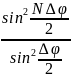 (5.2.а)
(5.2.а)