§ 5.1 Интерференция от двух источников

5.1.1. Суперпозиция волн от двух источников

Рассмотрим наложение волн одинаковой поляризации, порождаемых двумя гармоническими источниками S₁ и S₂ , совершающих колебания с одинаковой частотой ω₁ = ω₂ = ω.

В произвольной точке М волновые функции складываемых волн

ψ(x₁,t) = А₁ cos (ωt – kr₁ +α₁) = А₁ cos t)

ψ(x₂,t) = А₂ cos (ωt – kr₂ +α₂) = А₂ cos t)

Квадрат амплитуды результирующего колебания в точке М равен:

А² = + +2A₁ A₂ cos [ t) - t)] (5.1)

Видим, что определяющим здесь является значение разности фаз складываемых волн.

5.1.2. Понятие о когерентности

Условием стационарности интерференционной картины является

φ = [ t) - t)] = const

Волны называются когерентными, если их разность фаз имеет постоянное (но своё в каждой точке) значение или является закономерной функцией времени.

Когерентные волны могут быть получены только от когерентных источников c независящей от времени разностью фаз.

Если в (5.1) […] =0, то А = А₁ + А₂ ;

При […] = π, А = А₁ - А₂

У реальных источников излучения разность фаз не остаётся постоянной сколь угодно долго. У тепловых излучателей за время τ (10^-11 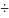10^-13)с она достигает значений π 2π. Величину τ называют временем когерентности. Оно в соответствие с теоремой о ширине полосы частот

подчиняется условию

τ = .

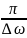За время наблюдения t τ среднее cos φ =0 и интенсивность результирующего поля I = I₁ + I₂ .

Используют также характерный параметр l_k = τ·υ_ф - длину когерентности.

5.1.3. Условия максимального (а) и минимального (б) ослабления волн

(а).

Полагая в (5.1) разность фаз раной нулю, имеем:

сos φ = 1, A_max =A₁ + A₂ и это при

k (r₁ - r₂ )= 2 πm, где m =0, 1, 2, 3…

Величину (r₁ - r₂ )= r называют геометрической разностью хода лучей. Т.к. k = , получаем условие для интерференционного максимума:

r = m λ (5.2)

(б).

При сos φ = -1 из (5.1) следует А² = 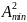= (A₁ –A₂)² или A_min = │A₁ – A₂│

Иначе: k (r₁ - r₂ )= (2m + 1)π Отсюда вытекает условие для минимума

r = (2m + 1)

5.1.4. Перераспределение энергии

Используя связь I A² выражение (5.1) запишем в виде:

I = I₁ + I₂ +2 cos φ

Усиление интенсивности при φ 0

При этом: I_max = ( + 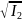)² для φ = 2πm

I_min = ( - )² для φ = (2m +1) π

Перераспределение интенсивности важнейшее свойство интерференции.

При I₁ = I₂ = I имеем: I_max = 4 I и также I_min = 0

§ 5.2 Стоячие волны

Стоячей волной называют суперпозицию двух встречных бегущих гармонических волн одинаковой поляризации, частоты и амплитуды.

Реализуется при интерференции падающей и отражённой волн.

5.2.1. Уравнение волны

Пусть ψ₁ = А₁ cos (ωt - kx) и ψ₂ = А₂ cos (ωt + kx), где А₁ = А₂ = А

Тогда: ψ = ψ₁ + ψ₂ = ∙2А cos kx cos ωt

Амплитудой стоячей волны является А_ст. = │2А cos kx│

Точки среды, где А_ст. = 0 называются узлами ст. волны.

Координаты узлов определим из условия kx =(2m +1)

х_уз. = (2m +1) (m =0, 1, 2, 3…)

Точки среды, где А_ст. = 2А называются пучностями ст. волны

Координаты пучностей определим из условия kx = πm

х_пуч.. = m (m =0, 1, 2, 3…)

Фаза стоячей волны. Между любыми ближайшими узлами фаза всех точек - одинакова и равна ωt. Она меняется скачком при переходе через узел.

5.2.2. Стоячая электромагнитная волна

Уравнения стоячей волны

Колебания совершают два вектора и . Они составляют правую тройку с вектором .

Волновые функции для складываемых волн:

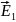(x,t) = E_o cos (ωt – kx)

₁ (x,t) = H₀ cos (ωt – kx) - у бегущей вправо волны

(x,t) = E_o cos (ωt + kx)

₂ (x,t) = - H_o cos (ωt + kx) - у встречной, влево бегущей волны

Суммируем: = + = 2 E_o cos kx cos ωt

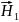= + = 2 H_o sin kx sin ωt

Видно, что эл. и магн. составляющая различаются по фазе на , а по времени соответственно на .

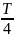5.2.5. Энергия стоячих волн

Поскольку групповые скорости первичной и отражённой волн противоположны, вектор Умова-Пойнтинга результирующей (стоячей) волны равен нулю:

= _пад.+ _отр. = w _g + w(- _g) = 0

Полная энергия колебаний в стоячей волне между узлами остаётся постоянной, она только периодически переходит из кинетической эн. в потенциальную и наоборот. Особенность этих энергий в стоячей волне, что они локализованы в разных частях системы и максимальны в разные моменты времени.

Объёмная плотность кин. энергии

w_k = ( )² = 2ρω²A² cos² kx ∙sin² ωt

w_п = ( )² = k² A² sin² kx ∙cos² ωt

w_k = w_п

Максимумы кин. энергии находятся в пучностях, а потенц. эн. в узлах волны.

В плоской стоячей электромагнитной волне

w_E = 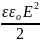= 2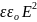 cos ²kx∙cos ²ωt

w_H = 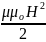= 2 sin² kx∙sin² ωt

Легко видеть в какие моменты времени и в каких областях пространства эти обёмные плотности энергии максимальны или минимальны.

5.2.6. Влияние границ на характер отражения

Важны при образовании ст. волны условия отражения от преграды: от этого зависит – будет на границе узел или пучность.

Два обстоятельства следует учитывать:

1. Ψ(x,t) – непрерывная функция координат;

2. Сумма потоков падающей и отражённой волне - постоянная величина.

Для упругих волн решающим оказывается так называемо волновое сопротивление среды (параметр z = ρс_s). При отражении от более плотной среды (z₁ z₂) на границе раздела возникает узел стоячей волны, при обратном соотношении (z₁ z₂) на границе раздела наблюдается пучность стоячей волны.

Для электромагнитной волны z = , (Для вакуума z = 377 Ом)

Более плотной диэлектрической средой оказывается диэлектрик с большим показателем преломления ( n = ). В итоге при при отражении волны от границы раздела сред для случая n₁ n₂ фаза вектора меняется на π, вектор фазу не изменит; в обратном случае n₁ n₂ неизменным окажется направление колебаний вектора , фаза вектора изменится на π. Тройка векторов , и всегда правовинтовая, в стоячей волне Е и Н колеблются со смещением по отношению друг к другу на .

5.2.7. Резонанс колебаний

В ограниченном пространстве при возникновении стоячей волны не подавляются колебания удовлетворяющие условию φ = 2πm

Выполнение этого для всех пар падающих и отражённых волн таким образом является резонансным.

Для “жёсткой” границы с обоих концов (для стержня)

Ψ(0,t) = 0 и Ψ(l,t) = 0

При этом λ_т = , ω_m =

Для “мягкой” границы c правого конца ( x=l)

Ψ(0,t) = 0 и Ψ(l,t) = Ψ_max(t)

λ_т = , ω_m =

Заданное распределение амплитуд в стоячей волне называют модой резонансной системы; наинизшая мода называется основной.