§ 2.3 Энергия эл.-м. Волны

2.3.1. Объёмная плотность энергии

Выражения для объёмных плотностей эл. и маг. полей нам известно:

w_э = ε_oεE², w_м = μμ_oН²

Полная энергия единицы объёма с учётом амплитудных соотношений и соответственно равенства w_э = w_м

w = w_э + w_м = ε_oε E² = μ_oμН²

Для среднего: = 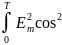(ωt – kx) dx =

= εε_o = μμ_o

Полная энергия: W = dV

2.3.2. Поток энергии. Вектор Пойнтинга

Если за поток энергии принять

Ф = -

количество энергии переносимое за ед. времени через некоторую площадку то плотностью потока энергии является

П =

Для электромагнитной волны указанная величина введена Пойнтингом. Это вектор сонаправленный вектору групповой скорости υ_г .

Как и для вектора Умова, используя величину объёмной энергии w , можно записать

= w _г

В вакууме _г = _ф = и

Подставив значение w, запишем:

= ε_oε = = [ ]

Итак:

= [ ] (2.3)

Величина I , определяющая среднее значение модуля в. Пойнтинга

I =

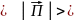
называется интенсивностью волны. Это - скаляр.

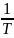
I = 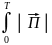dt = εε_o c = E_m H_m

I = Em Hm (2.4)

2.3.3. Переносимая мощность. Спектральная плотность мощности

Мощность энергии, излучаемая через поверхность S

N_s = dS_n

Полная мощность, переносимая через замкнутую поверхность

N^* = dS_n

Величины

N_ω = и N_‌λ =

соответственно характеризуют спектральную мощность приходящуюся на ед. интервал частоты или длины волны. Заметим, что нет естественных излучателей мощности на строго фиксированной частоте (длине) волны.

§2.4 Импульс эл.-м. Волны. Световое давление.

С эл.-м. волной связан определённый импульс. Если в слабо проводящей среде плотность тока проводимости j, то на ед. объёма действует сила

_ед.об. = [ ] = μ μ_о [ ]

Тогда: 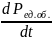= _ед.об. = =

Из релятивистского подхода должно следовать

= = =

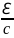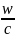При полном поглощении для импульса переданного среде через ед. площади в ед.времени (а это будет иметь смысл давления) получается:

Р_дав. =

При наличии отражения с коэфф. ρ

Р_дав. = (1 + ρ) = w (1 + ρ)

Гл.4 СЛОЖЕНИЕ ВОЛН

§ 4.1 Волновые пакеты (4.1.1). Бигармоническая волна (4.1.2)

4.1.1.

Гармоническая волна – идеальная модель. Процесс происходит за конечное время и формируется в ограниченном пространстве. В соответствии с принципом суперпозиции произвольную волну в линейной среде можно представить в виде группы (гармонических!) волн или волнового пакета.

Пример такого пакета – гармонический цуг со сложной спектральной плотностью амплитуды А(ω) = А_ω dω.

Временной и пространственный спектры оказываются идентичными

( А(k) = A_k dk ) при отсутствии дисперсии. В силу преобразования Фурье формы огибающих спектра и цугов взаимно обратимы.

Также в силу того, что фазовые скорости волн, образующих пакет,

одинаковы, его форма сохраняется. В противном случае, когда υ = f (ω),

волновой импульс “расплывается”.

4.1.2. Бигармоническая волна

Рассмотрим пространственный пакет из двух близких волн, когда:

А₁ = А₂ = А; ω₁ = ω – dω, ω₂ = ω + dω; k₁ = k – dk , k₂ = k + dk

Итак:

Ψ₁ (x,t) = А₁ cos [(ω – dω)t – (k – dk)x]

Ψ₂ (x,t) = А₂ cos [(ω + dω)t – (k +dk)x]

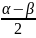Используя формулу cos α + cos β = 2 cos cos , получаем, пренебрегая бесконечно малыми

Ψ (x,t) = Ψ₁ + Ψ₂ = 2А cos (tdω - xdk) cos (ωt -k x)

Имеем в итоге амплитудно - модулированную гармоническую волну.

Ψ(t) представляет процесс, называемый биениями с периодом Т_мод. = .