
- •§ 1.1 Гармонические периодические волны
- •§ 1.2 Волновое уравнение для плоских волн
- •§ 1.3 Принцип суперпозиции (1.3.1) и спектр колебаний (1.3.2)
- •§ 2.1 Цепочка атомов и волновое уравнение для непрерывной среды
- •§ 2.2 Энергия упругих волн
- •§ 3.1 Волновое уравнение для эл.-м.Волн
- •§ 2.2 Характеристики эл.-м. Волны
- •§ 2.3 Энергия эл.-м. Волны
- •§2.4 Импульс эл.-м. Волны. Световое давление.
- •§ 4.1 Волновые пакеты (4.1.1). Бигармоническая волна (4.1.2)
- •§ 4.2 Групповая скорость. Соотношения Рэлея
- •§ 4.3 Соотношение неопределённости для волн
- •§ 4.4 Круговая и эллиптическая поляризация как результат
- •§ 5.1 Интерференция от двух источников
- •§ 5.2 Стоячие волны
- •§ 5.3 Положения геометрической и волновой оптики
- •§6.1 Принцип Гюйгенса-Френеля (6.1.1.). Метод зон Френеля (6.1.2.)
- •§ 6.2 Дифракция Фраунгофера.
- •§ 6.2 Дифракция Френеля
§ 3.1 Волновое уравнение для эл.-м.Волн
3.1.1.Уравнения Максвелла для волнового поля
Эл.-маг. волны это переменные эл. и маг. поля или иначе возмущения в виде полей. К их наличию при определённых условиях можно прийти исходя из классической теории Максвелла.
Система уравнений М. в дифф. форме:
rot
= -
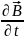 (I); div
(I); div
 = ρ (III);
= ρ (III);
rot
 =
=
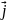 +
+
 (II); div
= 0 (IV);
(II); div
= 0 (IV);
= εo ε (V); = μo μ (VI); = γ (VII).
Однозначность их решений определяется начальными и граничными условиями.
Однажды возбуждённое эл.-м. поле может существовать само по себе, независимо от источников в форме волны в области, где нет свободных зарядов и нет переменных токов.
3.1.2. Волновое уравнение
Итак: пусть среда однородна и изотропна и нет в ней свободных зарядов и макротоков (j = 0, ρ = 0).
Допустим, что плоская волна распространяется в направлении оси ОХ.
Тогда:
функции
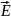 (х,t)
и
(х,t)
и
 (х,t)
и их проекции не будут зависеть от z
и
у,
а производные
(х,t)
и их проекции не будут зависеть от z
и
у,
а производные
 ,
,
 и
и

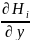 (здесь
i=
z,у,x)
будут
равны нулю.
(здесь
i=
z,у,x)
будут
равны нулю.
Учитывая, что:
[
rot
]x
=
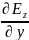 -
-
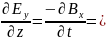 - μo
μ
- μo
μ
 ,
и выражая аналогично
,
и выражая аналогично
[ rot ]z и [ rot ]z ,
получают:
-
μo
μ
 =
=
 ,
εo
ε
,
εo
ε
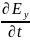 = -
= -
 (*)
(*)
εo
ε
 =
=
 ,
-
μo
μ
,
-
μo
μ
 =
-
=
-
 ,
(**)
,
(**)
Достаточно воспользоваться первой парой уравнений (*) для Ey и Hz , причём будем исключать наличие статических полей Ex и Hx
(т.
к. имеем
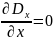 ,
,
 = 0).
Для
Ez
и
Hy
ситуация
подобна.
= 0).
Для
Ez
и
Hy
ситуация
подобна.
Дифференцируя
по t
второе
ур-е в (*), меняя порядок производной по
времени и координате (
 =
)
и
используя первое уравнение (*)
=
)
и
используя первое уравнение (*)
получаем:
 =
=
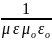
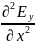
Приняв за квадрат фазовой скорости υ2 приходим к волновому уравнению для плоской волны Еу (х,t). Второе уравнение для Нz (х,t) получают аналогично. Итак:
= υ2 (2.1)
|
Волновое ур-е эл.-м. волны включает два независимых уравнения для Еу (х,t) и Нz (х,t), их вид – и есть решения (2.1):
Еу (х,t) = Еm cos(ωt - kx + φoE)
Hz (х,t) = Hm cos(ωt - kx + φoH)
В экспоненциальной форме
Еу
(х,t)
= Еm

Hz
(х,t)
= Hm
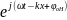
§ 2.2 Характеристики эл.-м. Волны
Поперечность эл.-м. волны
Мы пришли к тому, что плоская волна распространяется в направлении 0Х
При
этом:
= Еy ;
=
Hz
;
=
Hz
 или
,
волна поперечна.
или
,
волна поперечна.
0Х

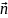 – нормали
к к её фронту. который
У0Z.
– нормали
к к её фронту. который
У0Z.
Фазовая скорость
υф
υр
=υ
и направлена по 0Х. υ =
 =
=

Тройка
векторов
 ,
и
- правовинтовая.
,
и
- правовинтовая.
В
вакууме
ε =1, μ =1, соответственно υф
 = с
– скорости света
= с
– скорости света
В
среде υф
=
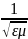 .
.
Синфазность волн
Если записать решения для Еу (х,t) и Hz (х,t) в экспоненциальной форме и
воспользоваться вторым уравнением пары (*), то
k
Hm

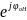 = εoε
ωEm
= εoε
ωEm
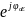 (***)
или
(***)
или
Равенство возможно только при условии,что
 =
=

Связь амплитуд
Из (***) также следует с учётом взаимосвязи ω, υ и k
 Em
=
Em
=
 Нm
Нm
В принципе, это связь между Е и Н.
Поляризация эл.-м. волны
Волна поперечна. Вектор колеблется в плоскости УХ, в пл. ZХ.
[ ] 0Х
Отметим, что в электромагн. волне силовым вектором является .
Отношение эл. и маг. сил, действующих на движущийся cо скоростью υ заряд в поле волны
 =
=
 ,
,
c – скорость света.

 =
υ2
=
υ2
