ч.3.2 ВОЛНЫ

ВВЕДЕНИЕ: ОБЩИЕ ХАРАКТЕРИСТИКИ И ПРЕДСТАВЛЕНИЯ О

ВОЛНОВЫХ ПРОЦЕССАХ

С волнами и волн. процессами встречаемся постоянно. Круг явлений очень широк.

Опр-е: Волной называется любое возмущение вещества или поля в пространстве, распространяющееся с конечной скоростью и обладающее (тем самым переносящее) энергией.

Волна – процесс во времени и в пространстве. Уравнение, которое даёт смещение колеблющихся частиц (или меняющихся величин) называется уравнением волны или волновой функцией - ψ(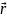 , t) = ψ(x,y,z, t). Часто это непростая функция.

а) При = _o = const и t t_o анализируют во времени волновую функцию ψ(t), называемую осциллограмой.

б) При t t_o имеем как бы мгновенный снимок волны в разных точках прост-ва r r_o .

Общая классификация

Она весьма условна. Волны различают:

1. По физической природе возмущения и виду среды:

а) механические (упругие, в том числе и звуковые)

1) в газах, жидкостях, твёрдых телах;

2) на поверхности, границе раздела сред;

б) электромагнитные

II. По виду волновой функции и типу изменяющихся физ. величин:

а) скалярные

например: в качестве волновой функции выступает давление ψ  p(r,t)

б) векторные (смещение связано с направлением)

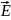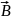ψ( ,t)  ( ,t) или ( ,t)

А также сюда отнесём:

1. гармонические,

2. негармонические

или:

3. линейные;

4. нелинейные (хар-ки зависят от амплитуды)

или:

5. стационарные ψ = ψ(х υt).

6. нестационарные.

Направление по которому задаётся вектор изменяющейся величины – это направление поляризации.

Для упругих волн выделяют: продольные и поперечные волны.

Световая волна может быть:

а) плоско поляризованной: ( ,t) – лежит в конкретной плоскости,

б) эллиптически (циркулярно) поляризованной: конец ( ,t) вращается по эллипсу или кругу.

III. По числу степеней свободы:

а) одномерные волны (плоские);

б) двухмерные (поверхностные) волны;

в) сферические (трёхмерные).

Иногда волны разделяют по виду волнового фронта:

а) плоские,

б) сферические,

в) цилиндрические

IV. По повторяемости процесса :

а) периодические;

б) не периодические;

в) уединённые (в том числе сохраняющиеся - солитоны).

Особую роль играют плоские, гармонические (периодические) волны.

ЛИТЕРАТУРА:

1. И.В. Савельев. Курс физики,тт.1, 2.

2. Т.И. Трофимова. Курс физики, 1998 г.

3. Т.С. Егорова, А.П. Жилинский, И.Д. Самодурова. Физика, ч.3.2:

Волновые процессы (конспект лекций), МТУСИ, 2004г.

Гл.1 ГАРМОНИЧЕСКИЕ ВОЛНЫ

§ 1.1 Гармонические периодические волны

1. Плоские волны

Такие волны возникают, если источник колебаний является гармоническим, а среда – линейной (изотропной).

Ψ(0,t) = A cos(ωt + φ_o) – пусть з–н колеб.источника

В случае т.н. плоской одномерной волны само смещение в т. x запишется через время запаздывания t_з = , а именно: t΄ → t +

Получим: Ψ(х, 0) = Ψ(х, t΄- t_з ) = Ψ(х, t) = A cos (ωt - 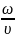x + φ_o) =

A cos (ωt - kx + φ_o) –уравнение гармонической плоской волны:

Ψ(х, t) = A cos (ωt - kx + φ_o)

В комплексной форме:

Ψ(х ,t) = А

Часто полагают φ_o равной нулю.

Очевидно, что Ψ(х, t) будет иметь одно и тоже значение, если x υt = const.

Характеристики волны:

А – амплитуда, k – волновое число (k = = )

Знаем: λ – длина волны (пространственный период), υ – фазовая скорость

ω – циклическая частота колебаний, Т – период колебаний (ω = ),

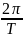причём: λ = υ ∙Т

Фазовая скорость находится из условия постоянства фазы:

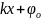(ωt – ) = const

Дифференцируем : ω dt –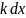 = 0

Или: = υ – фазовая скорость.

Если имеется затухание А = A_o е^{- δt} , аплитуда убывает, процесс не является строго гармоническим.

Плоская волна произвольного направления:

Ψ( ,t) = A cos (ωt – k_xx –k_yy –k_zz) = A cos (ωt – ).

2. Сферическая и цилиндрическая волны

Сферическая волна

Такая волна порождается точечным источником и распространяется во все стороны, амплитуда её уменьшается обратно пропорционально расстоянию, поскольку энергия проходит через большую поверхность.

Ψ( ,t) = A(r) cos (ωt – 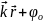), где A(r) =

Цилиндрическая волна

Волна порождается протяжённым источником колебаний (нить, тонкий цилиндр). Амплитуда А 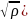, где ρ – полярный радиус.

Ψ(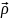 ,t) = A(ρ) cos (ωt – ),

§ 1.2 Волновое уравнение для плоских волн

Непосредственной подстановкой можно убедиться, что уравнение

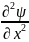= υ² (1.2)

Удовлетворяется, если Ψ(х ,t) = A cos (ωt - kx + φ_o) или комплексной форме Ψ(х ,t) = А

(1.2) - известное волновое уравнение. Это линейное дифф. уравнение второго в частных производных.

= -Аω² cos (ωt - kx + φ_o); = -Аk² cos (ωt - kx + φ_o); = υ²

Для волны произвольного направления = k_xx + k_yy + k_zz и

ψ(x,y,z) = ψ( ) соответственно:

ψ(x,y,z) = или

+ + = (1.2.а)

Для получения однозначного решения необходимо задание начальных и граничных условий!

Дисперсия

Соотношение υ² = определяет связь фазовой скорости, циклической частоты и волнового числа. Оно носит название дисперсионного уравнения. Зависимость ф. скорости от частоты (волнового числа) называют дисперсией. Это одна из важнейших сторон распространения волн в реальных средах.

Различают нормальную, аномальную дисперсии и отсутствие оной (нулевую дисперсию).

Разложение призмой белого света в спектр – проявление дисперсии.