Критерий Шапиро-Франчиа

Статистика критерия имеет вид:

,

,

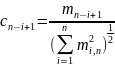где m_i,n – математическое ожидание i-й порядковой статистики стандартного нормального распределения.

Применяется аппроксимация:

,

где не искажает существенно критерий W’.

Используя аппроксимацию для квантиля стандартного нормального распределения, можно записать:

,

и для имеем:

.

При гипотеза нормальности отвергается. Критерий может применяться при больших значениях n.

Задание №5

ПОСТРОЕНИЕ ЭМПИРИЧЕСКОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ

Исходные данные: на практическом занятии.

1. Построить вариационный ряд: x₁, … , x_n.

2. Каждому значению вариационного ряда поставить в соответствие вероятность .

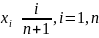3. Построить график эмпирического закона распределения.

4. На этом же графике для тех же значений x_i построить функцию нормального закона распределения.

5. Сравнить эмпирический и нормальный законы распределения по критерию Колмогорова по таблицам или формуле .

6. Сделать выводы.

Задание №6

ПОСТРОЕНИЕ ПАРАМЕТРИЧЕСКОГО ТОЛЕРАНТНОГО ИНТЕРВАЛА

Исходные данные приведены на лекции.

Построить параметрический толерантный интервал для законов распределения – нормального, полунормального, равномерного, рэлеевского, логистического, Пирсона.

1. Построить односторонний толерантный интервал для нормального закона распределения по приближенной формуле:

для R₃ = 0,95; 0,975; 0,99;

γ = 0,9; 0,95;

n = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.

2. Построить односторонние толерантные интервалы для равномерного, рэлеевского, логистического, Пирсона распределений по приближенной формуле:

,

где ,

P_R3 находится по таблицам квантилей распределения Пирсона для показателей асимметрии β₁ и β₂, приведенных в таблице 1.

Таблица 1

Распределение	β1	β2
Равномерное	0	1,8
Логистическое	0	4,2
Полунормальное	(0,995)2	3,869
Рэлеевское	(0,63)2	3,26
Пирсона (экспериментальное)	0	2,1

для указанных выше значений R3, γ, n.

Результаты расчетов внести в таблицы. Сравнить со случаем нормального закона распределения.

3. Проверить, какое значение вертикальной скорости самолета ТУ-154 в момент касания взлетно-посадочной полосы подтверждается с R3 = 0,95, γ = 0,9, n = 71, m = 0,8, S = 0,4, β₁ = 0, β₂ = 2,1 по формуле:

x_max = m + KS

при аппроксимации экспериментальных данных указанными законами распределения.

Задание №7

ПРОВЕРКА ГИПОТЕЗЫ О ЗНАЧЕНИИ ВЕРОЯТНОСТИ ВЫПОЛНЕНИЯ ТРЕБОВАНИЙ

Исходные данные приведены в лекции.

Построить доверительный интервал на параметрическую оценку вероятности выполнения требований. Проверить статистическую гипотезу R ≥ R₃ при R₃ = 0,95; γ = 0,9; x_доп = 1,5; x_доп = 1,6; x_доп = 1,7.

1. Рассчитать оценки:

.

2. Рассчитать коэффициент:

.

3. Построить доверительный интервал на оценку :

,

где 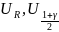– квантили стандартного нормального распределения.

4. Построить области принятия гипотез R > R₃, R < R₃, R = R₃, по соотношению:

и определить область, соответствующий K из (1).

5. Рассчитать точность статистического решения по соотношению:

при α = β= 1 – γ для

n = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100;

γ = 0,9; 0,95 и различных K из (1).

6. Результаты внести в таблицу и проанализировать.