МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Московский авиационный институт
(национальный исследовательский университет)»
Кафедра «Испытания летательных аппаратов»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К выполнению курсовых работ по курсу
«Математическая обработка результатов эксперимента»
д.т.н., профессор
Александровская Л.Н.
Кириллин А.В.
Москва 2016
СОДЕРЖАНИЕ РАБОТЫ
Целью выполнения курсовой работы является закрепление теоретического материала и получение практических навыков обработки результатов эксперимента.
Результатами эксперимента являются результаты летных испытаний самолета ТУ-154.
В качестве исследуемого параметра выбрана вертикальная скорость в момент касания взлетно-посадочной полосы (ВПП), лимитирующая надежность и безопасность автоматической посадки по III А категории.
Для обработки предоставляются три массива измерений вертикальной скорости (в м/с), полученных в различающихся условиях:
Посадка на ВПП с автоматическим сбросом газа
X1 = 0,7
X2 = 0,4
X3 = 0,9
X4 = 0,8
X5 = 1,5
X6 = 1,2
X7 =1,0
X8 = 1,2
X9 = 1,4
X10 = 1,1
X11 = 1,2
X12 = 0,8
X13 = 1,3
X14 = 1,2
X15 = 0,45
X16 = 1,4
Оценка качества в предельных эксплуатационных условиях
X17 = 1,3
X18 = 0,9
X19 = 1,1
X20 = 1,2
X21 = 1,1
X22 = 1,7
X23 = 0,6
X24 = 1,0
X25 = 1,6
X26 = 0,6
X27 = 0,4
X28 = 0,4
X29 = 0,8
X30 = 0,1
X31 = 0,5
X32 = 0,4
X33 = 0,6
X34 = 1,0
X35 = 1,3
X36 = 0,9
X37 = 1,0
X38 = 0,8
X39 = 0,2
X40 = 0,6
X41 = 1,0
X42 = 0,8
X43 = 1,0
Уточнение методики выполнения автоматического выравнивания
X44 = 1,3 X45 = 1,4 X46 = 0,5 X47 = 0,7 X48 = 0,7 X49 = 0,4 X50 = 1,3 X51 = 1,4 X52 = 0,1 X53 = 0,8 |
X54 = 0,7 X55 = 0,3 X56 = 0,4 X57 = 0,2 X58 = 0,4 X59 = 0,1 X60 = 0,7 X61 = 0,6 X62 = 0,1 X63 = 0,6 |
X64 = 0,7 X65 = 0,1 X66 = 0,7 X67 = 0,5 X68 = 1,1 X69 = 1,1 X70 = 0,1 X71 = 0,1 |
Задачей
обработки
является определение значения вертикальной
скорости
Vyдоп
такого,
что
Вер
с доверительной вероятностью γ = 0,95,
т.е. толерантного интервала для заданного значения R3.
На рис. 1 представлена структурная схема решения поставленной задачи.
Рис. 1. - Структурная схема решения поставленной задачи
В рамках приведенной структуризации студенты выбирают тему курсовой работы.
Защита курсовой работы проходит в форме кафедральной студенческой конференции.
ОФОРМЛЕНИЕ РАБОТЫ
Работа оформляется в электронном виде. На защиту предоставляется распечатка, дискета, иллюстративный материал, необходимый для доклада.
Работа должна содержать титульный лист, введение, теоретическую часть, экспериментальную часть, выводы, список использованной литературы.
На титульном листе помещается название института, кафедры, курса, работы, ФИО студента, преподавателя, группа студента.
Во введении анализируется роль и место выбранной частной задачи в общей задаче.
В теоретической части проводится аналитический обзор возможных методов решения частной задачи, выбор конкретного метода и алгоритма ее решения.
В экспериментальной части указывается, с помощью какого программного средства произведены расчеты, приводятся результаты расчетов.
В выводах анализируются полученные результаты и принятое на их основе решение.
Задание №1
ПРОВЕРКА СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
Исходные данные:
Имеется 4 группы результатов летных испытаний самолета ТУ-154, полученных при различающихся условиях.
n=16
Vy(м/с) = 0.7; 0.4; 0.9; 0.8; 1.5; 1.2; 1.0; 1.2; 1.4; 1.1; 1.2; 0,8; 1.3; 1.2; 0,45; 1.4
n=27
Vy(м/с) = 1.3; 0.9; 1.1; 1.2; 1.1; 1.7; 0.6; 1.0; 1.6; 0.6; 0.4; 0.4; 0.8; 0.1; 0.5; 0.4; 0.6; 1.0; 1.3; 0.9; 1.0; 0.8; 0.2; 0.6; 1.0; 0.8; 1.0
n=28
Vy(м/с) = 1.3; 1.4; 0.5; 0.7; 0.7; 0.4; 1.3; 1.4; 0.1; 0.8; 0.7; 0.3; 0.4; 0.2; 0.4; 0.1; 0.7; 0.6; 0.1; 0.6; 0.7; 0.1; 0.7; 0.5; 1.1; 1.1; 0.1; 0.1
n=60
m=0.8 м/с
=0.4
Вариант 1. Проверка однородности методом парных сравнений.
Рассчитать для каждой выборки m, S2, m3, m4 и показатели асимметрии и эксцесса по формулам:
;
;
;
;
;
;
.
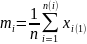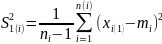Проверить нормальность законов распределения вероятностей выборок по критерию Крамера.
-
;
;
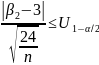где U1-α/2 – квантиль стандартного нормального распределения.
Проверить равенство дисперсий по критерию Фишера для двух наиболее различающихся оценок:
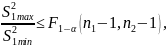
где
– соответственно максимальная и
минимальная из 4-х дисперсий;
n1, n2 – объем их выборок;
F1 – α – квантиль распределения Фишера.
Проверить равенство математических ожиданий для двух наиболее различающихся оценок:
,
где – оценки дисперсии, соответствующие mmax, mmin;
t1- α – квантиль распределения Стьюдента.
– округлить
до ближайшего меньшего числа.
Вариант 2. Проверка однородности методом парных сравнений
Повторить пункты 3-4 для сравнения результатов наиболее отличающихся от значений m = 0.8 м/c; σ = 0.4;
Проанализировать полученные результаты.
Задание №2
ПРОВЕРКА СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ МНОГОМЕРНЫМ МЕТОДОМ
Проверка равенства дисперсий по критерию Бартлетта.
;
;
;
;
При
гипотеза равенства дисперсий принимается.
Проверка равенства р математический ожиданий:
,
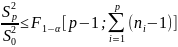где F1-α - квантиль распределения Фишера.
;
;
;
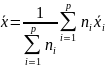При
гипотеза равенства математических
ожиданий принимается.
Задание №3
ПРОВЕРКА ОДНОРОДНОСТИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ ПО ДИСПЕРСИЯМ И МАТЕМАТИЧЕСКОМУ ОЖИДАНИЮ
Рассчитать оценки и проверить гипотезы однородности:
;
;
,
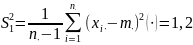где F1 – α – квантиль распределения Фишера;
α – уровень значимости.
В
числитель помещается большая из оценок
.
,
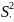где t – квантиль распределения Стьюдента;
m1 > m2;
.
При каком уровне значимости неравенство выполняется?
Рассчитать погрешности статистических решений по приближенным формулам:
;
при α = β = 0,05; 0,1;
n = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Результаты расчетов внести в таблицы и проанализировать.
Задание №4
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТНОЙ СКОРОСТИ САМОЛЕТА В МОМЕНТ КАСАНИЯ ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ
Исходные данные приведены в лекции.
Проверить возможность аппроксимации приведенных данных нормальным законом распределения по ряду критериев:
Критерий Шапиро-Уилка;
Критерий Шапиро-Франчиа.
Проанализировать полученные результаты: какой из критериев является более жестким.