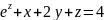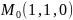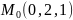найти экстремум заданной функции

Дана функция z=х
 .
Показать, что
.
Показать, что
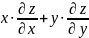 =z
=zВычислить значение производной сложной функции z=z(х,у) где

найти градиент функции
 в заданной точке
в заданной точке
 и его длину.
и его длину.
 ,
,
Вычислить
значения частны х производных функции
z(х;у),
заданной неявно, в данной точке

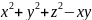 =2
=2

найти экстремум заданной функции

Дана функция z=х . Показать, что =z
Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. .
 ,
,

Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
3х-2у+z=хz+5

найти экстремум заданной функции

Дана функция z=(
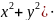 tg
tg .
Показать, что
=2z
.
Показать, что
=2z
3.Вычислить
значение производной сложной функции
z=z(х,у)
где

найти градиент функции в заданной точке и его длину. .
 ,
,
 ,
,
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
найти экстремум заданной функции

Дана функция z=arcsin
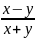 .
Показать, что
=0
.
Показать, что
=0Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. ,



Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
 =0
=0

найти экстремум заданной функции

Дана функция z=
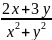 .
Показать, что
=-z
.
Показать, что
=-z
3.Вычислить
значение производной сложной функции
z=z(х,у)
где
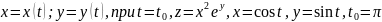
4.найти
градиент функции
в заданной точке
и его длину. , ;
;

Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
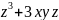 +3у=7
+3у=7

найти экстремум заданной функции

2,Дана
функция z= .
Показать, что
.
Показать, что
 =
=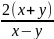
3.Вычислить
значение производной сложной функции
z=z(х,у)
где
 найти
градиент функции
в заданной точке
и его длину.
найти
градиент функции
в заданной точке
и его длину.
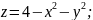

5.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
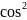 х+
у+
z=
х+
у+
z=

найти экстремум заданной функции
Дана функция z= . Показать, что =
3.Вычислить
значение производной сложной функции
z=z(х,у)
где
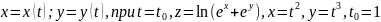 найти
градиент функции
в заданной точке
и его длину.
найти
градиент функции
в заданной точке
и его длину.
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
х+ у+ z=
найти экстремум заданной функции

Дана функция
 Показать, что
=3(
Показать, что
=3(
Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. ,


Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
 х
х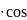 у+1
у+1

найти экстремум заданной функции
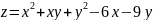
Дана функция z
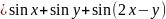 .
Показать, что
.
Показать, что
 =
=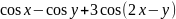
Вычислить значение производной сложной функции z=z(х,у) где
найти градиент функции в заданной точке и его длину.


Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
 =0
=0

найти экстремум заданной функции
 +2
+2
Дана функция
 Показать, что
Показать, что
 =0
=0Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. ,


Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
ху=
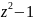

найти экстремум заданной функции
 +
+
Дана функция
 .
Показать, что
.
Показать, что
 =0
=0Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. ,


Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
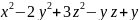 =2
=2
найти экстремум заданной функции

Дана функция
 Показать,
что 3у
Показать,
что 3у =0
=0Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. ,


Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
найти экстремум заданной функции
Дана функция Показать, что 3у =0
Вычислить значение производной сложной функции z=z(х,у) где
найти градиент функции в заданной точке и его длину. ,
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
найти экстремум заданной функции
Дана функция
 tg
tg Показать,
что 3у
Показать,
что 3у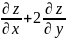 =0
=0Вычислить значение производной сложной функции z=z(х,у) где

найти градиент функции в заданной точке и его длину. ,
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
х

найти экстремум заданной функции

Дана функция
 .
Показать, что
=z
.
Показать, что
=zнайти производную от функции в точке по направлению вектора
 :.
:.
 ,
,
 ,
,
 .
. найти градиент функции в заданной точке и его длину. , . ,
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке 3
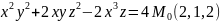
.найти производную от функции в точке по направлению вектора :. , , .
2.
найти экстремум заданной функции -
- -у+6х+3
-у+6х+3
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
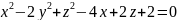
Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке

S: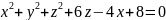
Вычислить значение производной сложной функции z=z(х,у) где
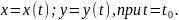

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
S: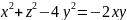

2.Найти производную от функции в точке по направлению вектора :
![]() ,
,
![]() ,
,
![]() .
.
найти экстремум заданной функции
 +2
+2Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
х+у+z+2=хуz

Вычислить значение производной сложной функции z=z(х,у) где
z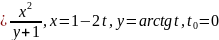
Найти производную от функции в точке по направлению вектора
.
![]() ,
,
![]() ,
.
,
.
2.найти экстремум заданной функции
![]()
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке

Вычислить значение производной сложной функции z=z(х,у) где

5.Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке


1.Найти производную от функции в точке по направлению вектора :
.
![]() ,
,
![]() ,
,
![]() .
.
2.найти
экстремум заданной функции
![]()
3.Вычислить
значение производной сложной функции
z=z(х,у)
где

4.Найти
уравнения касательной плоскости и
нормали к заданной поверхности S
в точке
S:

Дана функция . Показать, что =z
1.найти
производную от функции
в точке
по направлению вектора
:![]() ,
,
![]() ,
,
![]() .
.
2.найти
экстремум заданной функции
![]()
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке

Вычислить значение производной сложной функции z=z(х,у) где
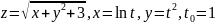
Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке S:
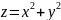
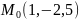
1.найти
производную от функции
в точке
по направлению вектора
:
![]() ,
,
![]() ,
,
![]() .
.
2.найти
экстремум заданной функции
![]()
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке


Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
S:

1.найти производную от функции в точке по направлению вектора
.
![]() ,
,
![]() ,
,
![]() .
.
2.найти
экстремум заданной функции
![]()
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке


4.Вычислить
значение производной сложной функции
z=z(х,у)
где

5.Найти
уравнения касательной плоскости и
нормали к заданной поверхности S
в точке
S: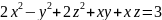

1.найти
производную от функции
в точке
по направлению вектора
:.
![]() ,
,
![]() ,
,
![]() .
.
2.найти
экстремум заданной функции![]()
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке


 Вычислить
значение производной сложной функции
z=z(х,у)
где
Вычислить
значение производной сложной функции
z=z(х,у)
где

5.Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
S:
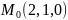
1.Найти
производную от функции
в точке
по направлению вектора
:![]()
![]()
![]()
2.Найти
экстремум заданной функции
![]()
![]()
3.Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
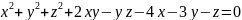
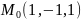
4.Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке S:

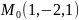
найти производную от функции в точке по направлению вектора :.
 ,
,
 ,
,
 .
.найти экстремум заданной функции
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке

Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
: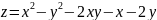
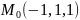
найти производную от функции в точке по направлению вектора :.
 ,
,
 ,
,
 .
.
найти экстремум заданной функции

Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
 =
=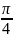
Вычислить значение производной сложной функции z=z(х,у) где
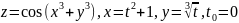
Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке


найти производную от функции в точке по направлению вектора :
 ,
,
 ,
,
 .
.найти экстремум заданной функции
![]()
Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
 =
=
Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
=2

найти производную от функции в точке по направлению вектора :.
 ,
,
 ,
,
 .
.
найти экстремум заданной функции

Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке

Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
S:

найти производную от функции в точке по направлению вектора :
найти экстремум заданной функции

Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке

Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
S:
найти производную от функции в точке по направлению вектора :



найти экстремум заданной функции

Вычислить значения частных производных функции z(х;у), заданной неявно, в данной точке
cos
(ху)+ cos
(хz)-sin
(уz)=1

Вычислить значение производной сложной функции z=z(х,у) где

Найти уравнения касательной плоскости и нормали к заданной поверхности S в точке
S:
Задание 1.Найти общий интеграл дифференциального уравнения.
1. 2.
2. ;
;
3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ;
;
7. ; 8.
; 8.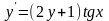 ;
;
9. ; 10.
; 10.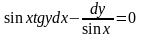 ;
;
11. ; 12.
; 12.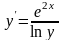 ;
;
13. 14.
14. ;
;
15. 16.
16.
17. 18
18
19.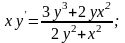 20.
20. ;
;
21.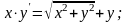 22.
22.
23. 24.
24.
25. 26.
26.
27. 28.
28.
29.
 ; 30.
; 30.
Задание 2. Найти частное решение дифференциального уравнения при следующих начальных условиях.
1.
 2.
2.
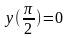 ;
;
3.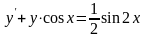 ;
;  4.
4.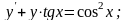
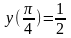 ;
;
5.
 6.
6.

7.
 8.
8.
 ;
;
9.
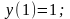 10.
10.
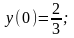
11.
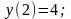 12.
12.

13.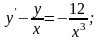
 14.
14.
15.
 16.
16.
17.
 18.
18. ;
;
19 20.
20.

21. 22.
22.

23. 24.
24.
25. 26.
26.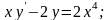
27. 28.
28.
29.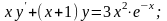 30.
30.
18. В задачах 18.1 – 18.20 найти частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям:
18.1. y'' – 7y' + 10y = 0; y(0) = 2; y'(0) = -1.
18.2.
y'' + 2y' + 10y = 0; y(![]() )
= 0; y'(
)
= 1.
)
= 0; y'(
)
= 1.
18.3. y'' – 6y' + 9y = 0; y(0) = 1; y' (0) = 0.
18.4. y'' + 8y' + 7y = 0; y(0) = 2; y'(0) = 1.
18.5. y'' + 9y = 0; y(π) = 0; y'(π) = -1.
18.6. y'' – 7y' + 12y = 0; y(0) = 2; у'(0)=-2.
18.7. y'' + 9y' = 0; y(0) = 1; y'(0) = -3.
18.8. y'' – 3y' + 2y = 0; y(0) = 0; y'(0) = 1.
18.9. y'' – 5y' + 6y = 0; y(0) = 5; y'(0) = 0.
18.10. y'' – 2y' + 5y = 0; y(0) = -1; y'(0) = 0.
18.11. y'' + 16y = 0; y(π) = -1; y'(π) = 0.
18.12. y'' + 10y' + 25y = 0; y(0) = 1; y'(0) = 1.
18.13. y'' – 6y' = 0; y(0) = 2; y'(0) = -2.
18.14. y'' – 4y' + 4y = 0; y(0) = 1; y'(0) = 3.
18.15. y'' – 8y' + 15y = 0; y(0) = 1; y'(0) = -2.
18.16. y'' – 4y' + 17y = 0; y( ) = 0; y'( ) = 1.
18.17. y'' – 2y' + y = 0; y(1) = 0; у'(1)=2
18.18. y'' + y = 0; y(π) = -1; y'(π) = -4.
18.19. y'' – 7y' + 6y = 0; y(0) = 2; y'(0) = 0.
18.20. y'' + 8y' + 16y = 0; y(0) = 1; y'(0) = 0.