Градиент

Наибольшая скорость пространственного изменения скалярного потенциала U называется градиентом и обозначается как grad U, или используя дифференциальный оператор набла. Применительно к прямоугольной декартовой системе координат, оси которых обозначим как X,Y,Z оператор набла имеет следующий вид

где i, j, k единичные векторы, направленные вдоль осей x,y,z соответственно.

Градиент потенциала вычисляется по формуле

Величина градиента, взятая с обратным знаком, называется напряжённостью поля, например, напряжённость электрического поля, обычно обозначаемая символом Е

Поток вектора.

Если принять, что в пределах малого элемента

{bmc Potok.bmp}Divergetion

выделенного на некоторой поверхности S, нормалью к которой является вектор dS, все векторы поляSymbol -W имеют одно и тоже значение, то элементарный поток вектора W определяется как скалярное произведение

WdS=WdS cos (A,dS).

Интеграл этой величины, взятый по всей поверхности выразит поток вектора Ф

.

В теории поля особое значение придаётся замкнутым поверхностям. Если эта поверхность находится в поле вектора W, поток может быть равен или не равен нулю. Если полный поток вектора через замкнутую поверхность равен нулю, то в этом случае количество векторных линий входящих в рассматриваемую поверхность равно количеству выходящих линий, следовательно, внутри рассматриваемого объёма нет физического агента, от которого линия поля могла бы начинаться или заканчиваться. Если поток замкнутого объема не равен нулю, то в этом случае в нём находится исток, или сток.

Циркуляция вектора. Для того, чтобы установить характер поля вводится понятие циркуляции вектора, которая определяет работу вектора по замкнутому пути. Если поле безвихревое – все векторы направлены в одну сторону, то циркуляция вектора W по замкнутому пути нулю

.

В противном случае поле является вихревым

Дивергенция. Чтобы охарактеризовать некоторый объем пространства с позиций наличия в нем стоков или истоков в теории поля вводится понятие дивергенции. Это предел, к которому стремится отношение полного потока вектора через замкнутую поверхность к величине этого объёма.

.

Дивергенция является скалярной величиной; она положительна, если линии поля начинаются в малом объёме, или отрицательна, если линии поля в этом объёме заканчиваются.

В электростатическом поле истоками являются положительные заряды, стоками -отрицательные. Следовательно дивергенция электрического поля имеет отличное от нуля значение в пунктах расположения зарядов. В других местах электростатического поля дивергенция отсутствует. В магнитном поле дивергенция вектора магнитной индукции всегда равна нулю, так как магнитных зарядов в изолированном виде в природе не существует

Определение дивергенции может быть выполнено как скалярное произведение оператора набла и вектора W.

.

Ротор вектора. Используя понятие циркуляции вектора, имеется возможность охарактеризовать любую точку рассматриваемого пространства с позиций характеристики поля. Для этого вводится понятие ротора вектора, который обозначают символом rot. Это вектор, направленный перпендикулярно некоторой площадке S определяемый как предел отношения величины циркуляции вектора к величине площадки при её беспредельном уменьшении. Если, например, площадка расположена на плоскости YZ, то ротор произвольного вектора A будет ориентирован перпендикулярно, т.е. вдоль оси X, и его длина составит

.

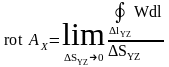В теории поля показано, что ротор вектора можно определять как векторное произведение дифференциального оператора  на вектор W

.

На основании рассмотренных понятий можно сформулировать условия существования потенциального и векторного поля.

В потенциальных полях градиент поля выражается посредством выражения (1.2). Тогда ротор градиента будет равен нулю, поскольку векторное произведение любого вектора на самого себя тоже равно нулю.

.

Отсутствие ротора говорит о том, что любая линия поля принципиально разомкнута, начиная у некоторого истока и заканчиваясь у некоторого стока. В точках расположения истоков и стоков дивергенция поля не равна нулю. Это второе условие существования безвихревого или потенциального поля. В электрических машинах такими полями являются потенциальное поле, характеризующее падение потенциала в обмотках, температурное поле, параметры которого определяются скалярной величиной – температурой.

Векторная величина W, не имеющая ротора, как правило, является градиентом некоторого скаляра, который называется скалярным потенциалом поля вектора W. В электрических машинах к этому можно отнести скалярный потенциал напряжённости электрического поля E в изоляции или токоведущих частях, а также скалярный потенциал вектора напряжённости магнитного поля H.

В вихревых полях линии поля замкнуты, поэтому невозможно указать расположение стока или истока, следовательно, дивергенция вектора будет равна нулю. Это является необходимым условием существования вихревого поля. Однако в любой точке пространства, где существует вихревое поле, ротор вектора не равен нулю. В этом случае его нельзя представить как градиент скаляра.

Встречаются векторные поля, у которых во всех точках ограниченного пространства нет ни ротора, ни дивергенции; такое поле обладает скалярным и векторным потенциалами. В таком смешанном поле имеются поверхности и линии равного скалярного потенциала (эквипотенциалы). Линии поля, касательные к которым будут указывать направление градиента скалярного потенциала в каждой точке, должны быть непременно замкнутыми, а поскольку дивергенция равна нулю, в поле нет ни истоков, ни стоков. Однако смешанное поле не имеет и ротора; другими словами, нельзя представить, чтобы замкнутая линия поля, где - либо стянулась в маленькую петлю-вихрь, предел бесконечного уменьшения которой определял бы величину ротора. Значит, все линии поля, оставаясь замкнутыми, имеют конечное протяжение. Обычно такие поля образуются вокруг областей чисто вихревых полей. Таково, например, магнитное поле снаружи проводника с током.

В электрических машинах особую роль играют магнитные поля. Известно, что магнитное поле образуется вследствие движения электрических зарядов в проводниках обмоток. Упрощённо можно считать, что магнитные силовые линии замыкаются вокруг вектора скорости движения электрических зарядов. Поэтому магнитное поле является вихревым. Однако пути замыкания силовых линий в значительной степени зависят от свойств окружающей среды. Поэтому расчёт магнитных полей в электрических машинах можно свести к определению путей замыкания магнитных силовых линий с учётом свойств электротехнических материалов, находящихся в магнитном поле.

Электромагнитное поле электромеханических систем характеризуется системой уравнений Максвелла:

где -напряжённость магнитного поля; -индукция магнитного поля;

-электрическое смещение; -напряжённость электрического поля;

, -абсолютная магнитная и диэлектрическая проницаемости среды соответственно;

-объёмная плотность зарядов;

-полная плотность тока, равная сумме плотности тока проводимости - , плотности тока переноса- , плотности тока смещения-

В изотропной среде имеют место следующие соотношения

-удельная проводимость среды.

Уравнения

характеризуют магнитные свойства электромагнитного поля. Первое из них указывает, что магнитное поле носит вихревой характер. Второе отражает факт остутствия магнитных зарядов и следовательно истоков, и факт непрерывности магнитного потока.

Проводящие среды электромеханических систем (медь, сталь, алюминий и др) обладают высокой проводимостью.Токи смещения и токи переноса для таких материалов не учитываются. Потому полная плотность тока принимается равной токам проводимости

.

Уравнения

характеризуют электрические свойства электромагнитного поля. Первое из них указывает, что изменение во времени магнитного поля приводит к возникновению электрического поля. Второе из них отражает факт наличия в электрическом поле истоков или стоков, каковыми являются электрические зарды.

Параметры характеризуют свойства среды. В зависимости от изменения этих параметров различают изотропнную и анизотропную среду а также линейную или нелинейную среды.

Уравнения магнитного поля постоянного тока в интегральной форме

В основе расчета магнитного поля постоянных токов лежит следующая система уравнений в интегральной форме:

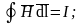
Эту систему следует дополнить выражением объемной плотности энергии магнитного поля

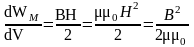
Первый интеграл известен под названием закона полного тока: