Действующее значение периодической несинусоидальной величины.

Действующее значение – среднее квадратичное значение за период

Всё сказанное в дальнейшем (формулы) будет справедливо и для e, u, J.

Пусть есть несинусоидальный ток, разложим его в ряд Фурье.

Где i_k – чистые синусоиды. Подставим формулу (2) в формулу (1), т.к. под интегралом будем иметь квадрат суммы, в выражении (1) должны появиться квадраты слагаемых и удвоенное произведение. С учетом этого выражение (1) примет вид:

– квадрат действующего значения k –й гармоники;

;

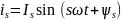
Если q и s подставить в выражение (*) и провести тригонометрические преобразования, в результате под знаком интеграла получим алгебраическую сумму косинусов. Результирующий график будет выглядеть:

И интеграл за период (площадь) будет равен нулю. Поэтому действующее значение периодической несинусоидальной функции будет равно квадратному корню из суммы квадратичных значений постоянной составляющей и всех гармоник.

Активная мощность при периодических несинусоидальных напряжении и токе.

Активная мощность – средняя мощность за период.

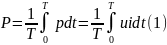
(2)

Подставим (2) в (1) в результате получим квадраты сумм гармоник, поэтому в выражении для активной мощности должны появиться квадраты и удвоенные произведения.

- интеграл дает нулевую площадь => =0

Поэтому активная мощность в нашем случае будет равна только первому слагаемому.

Активная мощность всей цепи равна сумме активных мощностей постоянной составляющей и всех гармоник.

Но для мгновенная мощность потребляемая цепью p=ui (несинусоидальные), т.к. в формуле нет интеграла нельзя пользоваться методом наложения, и общая мгновенная мощность не равна сумме мгновенных мощностей гармоник.

Чтобы количественно охарактеризовать эффективность передачи мощности, введен коэффициент мощности

α = 0 при условии, что числитель дроби равен нулю следовательно активная мощность не передается p = 0.

α = 1 в этом случае P=S. Если цепь содержит только активные R и G, то α =1

Если в цепи действуют «чистые» синусоидальные напряжения и токи, никаких высших гармоник нет, то коэффициент α = cosφ.

Высшие гармоники приводят к снижению α по сравнению с синусоидальным случаем, поэтому генераторы ЭДС конструируют так, чтобы их ЭДС по форме приближалась к синусоиде.

У электрических машинных генераторов форма ЭДС максимально приближенна к синусоиде, но в настоящее время эти генераторы заменяются статическими полупроводниковыми преобразователями. У них форма далека от синусоиды, поэтому дополнительно используют фильтры.

Высшие гармоники вызывают потери мощности, т.е. понижают кпд. Однако, в радиотехнике, автоблокировке, СЦБ и т.п. работают с несинусоидальными напряжениями и токами. Эти устройства маломощные и требования высокого кпд и cos φ здесь не критично.

Особенности поведения высших гармоник в трехфазных цепях.

Имеем трехфазный электромагнитный генератор, пусть его фазные ЭДС периодические несинусоидальные. Из-за симметрии их кривых, они будут содержать только нечетные гармоники. Предположим так же, что генератор симметричен, поэтому кривая ЭДС во всех фазах имеет одинаковую амплитуду, но в разных фазах она сдвинута на 120̊. Разложим ЭДС в ряд Фурье и посмотрим как будут себя вести различные гармоники.

1. Основная (первая) гармоника измениться с той же частотой, что и результирующая ЭДС и будет сдвинута в соседних фазах на угол 120̊

2. Высшая гармоника (k)

Её период в k-раз меньше периода основной гармоники, а частота в k-раз больше.

1. Гармоники, у которых порядок (номер) кратен 3.

ЭДС высшей к-й гармоники сдвинута в соседних фазах на угол к*120̊. Здесь ЭДС во всех трех фазах совпадет по фазе, а вектора этих ЭДС параллельны друг другу, т.е. эти гармоники составляют нулевую последовательность.

2. Высшие гармоники порядка k, для которых k-1 кратен 3 (делится на 3), например 7-я гармоника. Они составляют прямую последовательность. Их векторная диаграмма представляет собой: модули одинаковы; прямая последовательность.

3. Высшие гармоники, для которых k+1 кратен 3, например 5-я гармоника. Для них векторная диаграмма выглядит следующим образом: Вектора составляют обратную последовательность, в сумме

Из этих свойств высших гармоник вытекает ряд особенностей их поведения в трехфазных цепях:

1. Пусть обмотки генератора соединены в треугольник, здесь сумма фазных ЭДС (их первых гармоник) равна нулю, т.к. первые гармоники составляют прямую последовательность. Это имеет место для всех гармоник, которые образуют прямую или обратную последовательности.

2. Гармоники ЭДС, порядок которых кратен 3, совпадают по фазе во всех фазных обмотках генератора, поэтому их сумма не равна нулю, т.к. они составляют нулевую последовательность. Эта суммарная ЭДС создает ток, который циркулирует по треугольнику, т.е. внутри генератора и во внешнюю цепь не выходит. Падение напряжения в обмотках, обусловленное этим током, компенсируется соответствующими ЭДС, поэтому напряжение на зажимах трехфазного генератора линейные и фазные не содержат гармоник, порядок которых кратен 3. Поэтому напряжения на зажимах генератора как линейные, так и фазные не содержат гармоник кратных трём. Такая же ситуация возникает при соединении обмоток трансформатора треугольником.

Теперь рассмотрим случай, когда обмотки генератора или трансформатора соединены звездой с нейтральным проводом, так звездой соединена и нагрузка. Предположим, что система фазных ЭДС генератора симметрична, тогда в фазных напряжениях U_AO, U_BO, U_CO содержаться гармоники кратные трём, но в линейных напряжениях, которые равны разности фазных напряжений, гармоники кратные трем отсутствуют.

Это приводит к тому, что отношение линейного напряжения к фазному:

В фазных напряжения есть 3-е гармоники, а в линейных нет, следовательно знаменатель возрастает, дробь уменьшается.

Но в линейном проводе будет протекать ток с гармониками кратными трем. Этот ток при определённых условиях может достичь больших значений.

Теперь уберем нейтральный провод, в этом случае в токах, протекающих в линейных проводах, гармоник кратных трем не будет (нет нейтрали => им не замкнуться). Но в этом случае, хотя токов нет между нейтральными точками 0 и 0’ возникает напряжение тройной частоты, которое может достигнуть опасных для жизни человека значений.

Вывод: поэтому для устранения этих нежелательных явлений нужно пытаться локализовать гармоники кратные трем в генераторе или трансформаторе, т.е. соединить их обмотки треугольником. Использование трансформатора дает гальваническую развязку генератора от нагрузки.

В технике и транспорте так же используют несинусоидальные периодические напряжения и токи, которые не могут быть разложены в ряд Фурье. Например биение колебаний, модулированные колебания.