2. Пример расчета радиальной (круговой) скп обсервованного места
судна.
Дано: mлп1 = ±2,5 мили; mЛлп2 = ±1,0 мили; θ = 43°; M0 – ?
Решение: по формуле
Если теперь из обсервованного места судна на путевой карте провести окружность радиусом R = M0 = 4,0 мили, то можно сказать, что фактическое место судна находится в пределах площади этой окружности с вероятностью
Р = 63% (0,63).
3. Порядок расчета и построения эллипса погрешностей:
Точность определения места судна (обсервации) оценивается эллипсом ошибок или средней квадратической ошибкой точки.
Расчет и построение эллипса ошибок могут быть выполнены различными способами. В приводимых примерах решение выполнено с использованием смещения линий положений.
Порядок расчета и построения эллипса ошибок.
1. Рассчитывается смещение линий положения по формулам:
Δn₁ = m₁/g₁
Δn₂ = m₂/g₂
2.Рассчитывается угол пересечения линий положения θ°
(всегда менее 90°, т.е. если θ° > 90°, необходимо 180° - θ°).
3. Рассчитываются сумма и разность полуосей эллипса ошибок по формулам:
а + b =(1/sinθ)√ Δn₁2 + Δn₂2 + 2 Δn₁ ∙ Δn₂ ∙ sinθ
а – b = (1/sinθ)√ Δn₁2 + Δn₂2 ─ 2 Δn₁ ∙ Δn₂ ∙ sinθ
4.Рассчитываются полуоси эллипса ошибок:
a = ((a +b) + (a-b))/2
b = ((a +b) ─ (a-b))/2
5.Рассчитывается угол ориентировки большой полуоси эллипса ошибок относительно второй линии положения:
tg2φ
= sin2θ/((Δn₁²/Δn₂²)+cos2θ)
6.Рассчитывается средняя квадратическая ошибка обсервованного места:
M0 = (1/sinθ)√ Δn₁2 + Δn₂2
7.Строится эллипс ошибок:
• от второй линии положения откладывается в острую часть угла θ° угол φ° и проводится линия, соответствующая направлению большой оси эллипса;
• по этому направлению в обе стороны от обсервованной точки откладывается величина большой полуоси а, в перпендикулярном направлении —
величина малой полуоси эллипса ошибок b;
• через концы отложенных полуосей проводится эллипс ошибок.
Пример. Рассчитать и построить эллипс ошибок и среднюю квадратическую ошибку места судна, определенного по двум пеленгам, взятым по магнитному компасу:
ОКП1 = 71°,0; ОКП2 = 196°,0; ΔМК = - 2°,0.
Средние квадратические ошибки во взятии пеленгов m₁ = m2 = = ±0°,8. С карты снято расстояние до ориентиров, пеленги которых брались:
D₁ = 15,4 мили D2 = 10,1 мили.
Решение.
1. Рассчитываем смещения линий положения:
Δn₁ = (m1 ∙ D1)/57,3 = (0.8°∙15.4)/57.3 ≈ 2.2 кб
Δn₂ = (m2 ∙ D2)/57,3 = (0,8°∙10,1)/57,3 ≈ 1,4 кб
Рассчитываем угол пересечения линий положения:
θ° = 196° — 71° = 125°; θ'= 55°
Рассчитываем сумму и разность полуосей эллипса ошибок:
а ± b = (1/0,8) ∙√ 4,6 + 2,0 ± 2∙2,2∙1,4∙0,8;
а ± b = 1,2√6,6 ± 5,0;
а + b = 1,2√11,6 = 4,1 кб
а – b = 1,2√1,6 = 1,5 кб
Рассчитываем полуоси эллипса:
а = 2,8 кб b = 1,3 кб
5. Рассчитываем угол ориентировки эллипса ошибок:
tg 2φ = 0,9/((4,6/2,0)-0,3) = 0,45
2φ ≈24° ⟹ φ ≈ 12°
6. Рассчитываем среднюю квадратическую ошибку определения места судна:
M0 = (1/sinθ)√ Δn₁2 + Δn₂2
М=1,2√4,6 + 2,0 = 1,2 √ 6,6 = 3,1 кб
7. Строим эллипс ошибок:
- от второй линии положения откладываем φ = 12° (рис. 1) и проводим направление большой оси;
- по направлению большой оси откладываем а = 2,8 кб и в перпендикулярном направлении b = 1,3 кб;
- проводим эллипс ошибок.
Построение можно выполнять на специально подготовленном бланке
(Бланк 1).
Теоретическая вероятность нахождения места судна внутри эллипса ошибок около 39%. Вероятность того, что место судна находится внутри радиуса круга М0 изменяется от 63,2 до 68,3% и зависит от соотношения полуосей (ИП2 – ИП1 =θ)
Как счисление пути судна, так и обсервация сопровождаются погрешностями, что обуславливает несовпадение обсервованного места со счислимым, отнесенным к моменту обсервации. Расхождение одномоментных координат счислимого и обсервованного мест судна называется невязкой места судна.
Невязка счисления Элементы невязки счисления
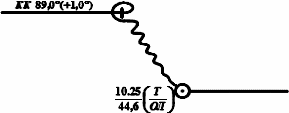
Рис. 1 Нанесение знака обсервации на карту.
Она характеризуется направлением от счислимого места к обсервованному и расстоянием С между ними. При графическом счислении пути судна невязка изображается волнистой линией, затухающей от счислимого места к обсервованному. Время и отсчет лага подписываются у обсервованного места.
Обсервованное место судна, полученное с точностью, превышающей точность счислимого места в три и более раза, принимается за исходную точку для дальнейшего счисления. Этим условиям, как правило, соответствуют обсервации, полученные по видимым ориентирам при прибрежном плавании, а также обсервации, полученные с помощью высокоточных радионавигационных и спутниковых навигационных систем.
При записи обсервации в судовом журнале направление невязки указывается с точностью до 1, а ее величина — с точностью до 0,1 мили. Например, С = 145° — 1,2 мили.
Если обсервованное место не принимается в качестве исходного для дальнейшего счисления, то на карту наносится знак обсервации и отмечается счислимое место судна на момент обсервации, около которого подписывается время и отсчет лага. Стрелкой от обсервованного места к счислимому показывается одномоментность обоих мест. В судовом журнале сведения о невязке заключаются в скобки, например,
(С = 215° — 4,2 мили).
Обработка серии неравноточных измерений.
|
ИП1 |
ИП2 |
ИП3 |
ИП4 |
ИП5 |
ИП6 |
ИП7 |
|
ИП1 |
ИП2 |
ИП3 |
ИП4 |
ИП5 |
ИП6 |
ИП7 |
1 |
46,5° |
47,6° |
47,8° |
45,8° |
45,8° |
47,9° |
45,4° |
51 |
75,7° |
76,4° |
74,4° |
76,2° |
76,2° |
74,3° |
75,0° |
2 |
11,7 |
11,7 |
11,5 |
10,8 |
11,4 |
10,5 |
11,6 |
52 |
219,1 |
218,5 |
219,0 |
220,6 |
219,1 |
218,5 |
217,8 |
3 |
278,6 |
279,6 |
279,0 |
279,4 |
279,0 |
277,5 |
277,2 |
53 |
146,1 |
146,5 |
146,7 |
146,6 |
146,1 |
145,9 |
146,1 |
4 |
127,5 |
126,8 |
128,1 |
128,6 |
128,0 |
127,9 |
127,0 |
54 |
200,7 |
200,0 |
201,5 |
201,1 |
201,5 |
200,8 |
201,6 |
5 |
241,9 |
241,5 |
241,8 |
241,5 |
240,6 |
241,8 |
242,2 |
55 |
274,4 |
275,2 |
275,0 |
275,2 |
275,6 |
275,0 |
274,9 |
6 |
266,2 |
265,5 |
265,9 |
265,6 |
267,1 |
267,0 |
266,4 |
56 |
77,6 |
78,4 |
78,9 |
78,7 |
77,4 |
78,0 |
78,1 |
7 |
95,5 |
94,1 |
94,5 |
94,6 |
96,5 |
94,3 |
95,3 |
57 |
212,0 |
213,4 |
213,0 |
212,5 |
212,6 |
210,9 |
212,4 |
8 |
199,2 |
200,0 |
200,2 |
200,3 |
200,3 |
198,4 |
200,6 |
58 |
33,3 |
33,0 |
32,1 |
33,2 |
34,2 |
33,7 |
33,9 |
9 |
31,0 |
30,4 |
29,7 |
31,7 |
31,3 |
29,9 |
31,3 |
59 |
172,0 |
172,1 |
171,2 |
172,4 |
173,2 |
170,5 |
171,7 |
10 |
111,2 |
112,0 |
111,8 |
110,6 |
112,1 |
111,0 |
112,3 |
60 |
88,0 |
87,6 |
87,9 |
87,2 |
89,1 |
88,0 |
88,2 |
11 |
124,1 |
124,5 |
122,7 |
125,1 |
124,0 |
124,1 |
124,8 |
61 |
66,9 |
66,7 |
66,3 |
67,1 |
65,6 |
67,5 |
67,3 |
12 |
317,6 |
317,1 |
317,0 |
319,1 |
317,0 |
317,0 |
317,7 |
62 |
109,2 |
108,6 |
107,7 |
108,1 |
109,7 |
108,9 |
110,1 |
13 |
306,2 |
306,6 |
305,9 |
304,9 |
307,0 |
306,6 |
306,5 |
63 |
89,5 |
88,3 |
90,9 |
89,5 |
88,5 |
88,8 |
90,7 |
14 |
117,6 |
118,5 |
118,9 |
117,6 |
116,9 |
118,2 |
117,0 |
64 |
99,7 |
98,8 |
99,6 |
101,0 |
99,9 |
100,6 |
98,9 |
15 |
152,5 |
152,2 |
154,0 |
152,8 |
153,7 |
151,8 |
152,9 |
65 |
287,5 |
287,5 |
287,9 |
287,2 |
286,1 |
286,5 |
286,9 |
16 |
132,5 |
132,2 |
133,4 |
133,2 |
131,3 |
131,6 |
131,6 |
66 |
58,6 |
58,3 |
57,6 |
58,6 |
58,3 |
58,7 |
58,9 |
17 |
98,8 |
97,7 |
99,6 |
100,2 |
100,2 |
97,5 |
100,2 |
67 |
68,8 |
68,4 |
70,3 |
68,3 |
67,5 |
69,9 |
68,7 |
18 |
226,9 |
227,4 |
225,7 |
228,2 |
227,0 |
226,5 |
227,0 |
68 |
51,5 |
51,6 |
51,7 |
52,9 |
52,1 |
52,5 |
53,0 |
19 |
150,0 |
150,0 |
149,2 |
150,3 |
150,4 |
149,6 |
150,1 |
69 |
307,4 |
307,8 |
308,3 |
308,8 |
308,1 |
306,9 |
307,7 |
20 |
202,6 |
203,3 |
203,0 |
203,0 |
202,8 |
201,2 |
201,9 |
70 |
216,4 |
216,1 |
216,1 |
215,8 |
214,9 |
216,7 |
217,1 |
21 |
33,5 |
32,4 |
34,2 |
32,4 |
32,2 |
33,4 |
33,1 |
71 |
305,2 |
305,3 |
305,2 |
304,8 |
304,1 |
304,9 |
305,8 |
22 |
274,3 |
272,9 |
273,7 |
273,5 |
275,0 |
274,6 |
273,7 |
72 |
311,4 |
310,4 |
311,6 |
310,7 |
310,3 |
311,6 |
310,2 |
23 |
134,7 |
133,7 |
133,5 |
134,7 |
133,5 |
133,4 |
133,8 |
73 |
215,4 |
215,1 |
214,9 |
215,3 |
216,7 |
214,4 |
215,6 |
24 |
300,1 |
299,8 |
299,9 |
301,1 |
299,8 |
299,0 |
298,6 |
74 |
193,6 |
194,2 |
194,4 |
194,9 |
192,8 |
194,4 |
193,1 |
25 |
322,6 |
321,8 |
321,2 |
321,5 |
322,7 |
322,5 |
321,1 |
75 |
222,1 |
222,3 |
223,2 |
223,2 |
222,7 |
223,4 |
223,0 |
26 |
168,1 |
168,0 |
169,3 |
167,7 |
167,0 |
169,4 |
168,1 |
76 |
117,0 |
115,8 |
116,9 |
118,0 |
117,7 |
116,2 |
117,4 |
27 |
22,9 |
23,6 |
21,8 |
22,2 |
23,2 |
22,8 |
23,3 |
77 |
280,3 |
281,4 |
279,6 |
279,0 |
280,3 |
280,1 |
280,3 |
28 |
355,2 |
356,1 |
356,1 |
355,8 |
354,1 |
355,1 |
356,2 |
78 |
302,3 |
303,1 |
300,9 |
301,7 |
303,6 |
301,1 |
303,3 |
29 |
76,2 |
77,3 |
76,6 |
77,3 |
76,8 |
77,7 |
75,4 |
79 |
104,0 |
103,1 |
104,8 |
103,3 |
102,7 |
104,5 |
104,3 |
30 |
217,2 |
216,5 |
215,8 |
215,9 |
216,0 |
217,1 |
216,6 |
80 |
140,3 |
141,6 |
140,6 |
141,4 |
140,2 |
141,5 |
140,2 |
31 |
276,6 |
275,2 |
276,1 |
276,7 |
276,9 |
275,5 |
277,5 |
81 |
280,6 |
279,3 |
279,3 |
280,1 |
280,7 |
280,5 |
280,6 |
32 |
227,9 |
226,5 |
228,0 |
228,9 |
229,1 |
228,3 |
227,0 |
82 |
99,2 |
99,2 |
98,7 |
99,3 |
99,9 |
99,0 |
99,0 |
33 |
183,2 |
182,7 |
182,5 |
183,1 |
181,8 |
182,1 |
184,6 |
83 |
332,2 |
332,8 |
331,7 |
332,4 |
331,3 |
332,4 |
332,0 |
34 |
249,4 |
247,9 |
250,1 |
248,6 |
249,5 |
250,3 |
250,1 |
84 |
173,9 |
172,4 |
175,3 |
173,9 |
174,0 |
173,5 |
173,3 |
35 |
89,4 |
89,7 |
88,5 |
89,9 |
89,4 |
90,7 |
89,5 |
85 |
285,6 |
287,1 |
285,2 |
285,1 |
286,6 |
284,7 |
285,2 |
36 |
138,0 |
138,2 |
137,7 |
137,4 |
137,2 |
138,6 |
137,3 |
86 |
341,2 |
340,6 |
342,1 |
340,4 |
342,2 |
341,7 |
341,7 |
37 |
22,8 |
23,7 |
21,6 |
23,1 |
22,3 |
23,2 |
23,3 |
87 |
341,1 |
342,0 |
342,4 |
341,6 |
341,3 |
340,4 |
341,1 |
38 |
49,0 |
47,7 |
50,3 |
47,7 |
48,7 |
48,4 |
50,0 |
88 |
272,3 |
271,9 |
273,5 |
272,7 |
272,3 |
272,3 |
270,9 |
39 |
156,8 |
156,9 |
157,7 |
155,8 |
155,9 |
155,6 |
158,1 |
89 |
201,5 |
201,3 |
201,4 |
200,5 |
202,0 |
201,0 |
200,3 |
40 |
296,4 |
297,3 |
295,7 |
295,9 |
295,9 |
297,8 |
295,4 |
90 |
194,7 |
194,0 |
194,7 |
193,8 |
195,5 |
196,1 |
195,4 |
41 |
147,6 |
148,8 |
148,5 |
148,3 |
148,9 |
146,6 |
148,2 |
91 |
36,8 |
37,1 |
36,2 |
37,2 |
35,5 |
35,6 |
36,1 |
42 |
103,3 |
102,0 |
104,6 |
102,1 |
104,7 |
102,2 |
104,5 |
92 |
131,8 |
132,0 |
132,5 |
133,2 |
130,8 |
130,8 |
130,4 |
43 |
199,1 |
200,1 |
199,0 |
200,1 |
197,7 |
199,0 |
197,6 |
93 |
169,5 |
168,3 |
168,1 |
168,2 |
170,3 |
169,0 |
170,9 |
44 |
176,3 |
175,5 |
177,7 |
175,2 |
177,1 |
175,0 |
175,5 |
94 |
200,6 |
199,2 |
201,1 |
200,6 |
200,6 |
202,0 |
199,8 |
45 |
120,9 |
121,2 |
120,2 |
119,7 |
121,1 |
120,7 |
120,0 |
95 |
246,0 |
246,5 |
246,7 |
247,3 |
244,5 |
245,5 |
246,5 |
46 |
109,3 |
109,1 |
108,2 |
107,9 |
109,8 |
108,6 |
108,3 |
96 |
106,4 |
107,8 |
107,4 |
106,6 |
105,0 |
106,0 |
106,4 |
47 |
224,4 |
224,0 |
223,6 |
224,8 |
223,7 |
223,3 |
225,5 |
97 |
60,6 |
61,6 |
59,4 |
59,5 |
60,7 |
61,6 |
62,0 |
48 |
302,6 |
301,1 |
303,1 |
302,6 |
302,8 |
301,7 |
304,0 |
98 |
129,2 |
128,2 |
128,6 |
129,3 |
130,3 |
130,1 |
129,9 |
49 |
82,1 |
81,7 |
81,9 |
82,4 |
82,9 |
81,3 |
82,8 |
99 |
157,5 |
158,0 |
157,5 |
158,5 |
156,8 |
157,6 |
157,7 |
50 |
64,9 |
63,7 |
64,4 |
64,8 |
65,9 |
65,3 |
64,5 |
100 |
102,2 |
103,0 |
100,9 |
101,8 |
103,5 |
100,9 |
102,9 |
Рассчитать среднюю квадратическую погрешность места судна, найденного по двум линиям положения. Построить эллипс погрешностей.
№ варианта |
КП1 |
КП2 |
ΔГК |
m1 |
m2 |
D1 |
D2 |
1 |
324,0 |
44,0 |
+1,0 |
1,7 |
1,7 |
15,9 |
10,8 |
2 |
125,0 |
174,0 |
-1,0 |
1,6 |
1,6 |
20,6 |
19,2 |
3 |
36,0 |
102,0 |
+3,0 |
1,5 |
1,5 |
16,3 |
18,4 |
4 |
220,0 |
275,0 |
+1,0 |
1,4 |
1,4 |
12,8 |
9,8 |
5 |
48,0 |
110,0 |
-1,0 |
1,3 |
1,3 |
9,4 |
7,9 |
6 |
05,5 |
336,5 |
+1,5 |
1,2 |
1,2 |
15,6 |
13,8 |
7 |
56,0 |
350,0 |
-2,0 |
1,1 |
1,1 |
8,9 |
11,7 |
8 |
165,0 |
224,0 |
+2,0 |
1,0 |
1,0 |
10,2 |
8,6 |
9 |
318,0 |
258,0 |
-3,0 |
0,9 |
0,9 |
14,7 |
10,3 |
10 |
52,0 |
04,0 |
+3,0 |
0,8 |
0,8 |
18,5 |
16,1 |
№ варианта |
КП1 |
КП2 |
ΔГК |
m1 |
m2 |
D1 |
D2 |
11 |
324,5 |
44,5 |
+1,5 |
1,3 |
1,3 |
14,9 |
10,3 |
12 |
123,0 |
174,0 |
-1,0 |
1,4 |
1,4 |
22.0 |
17,4 |
13 |
36,5 |
102,5 |
-1,5 |
1,3 |
1,3 |
14,6 |
16,2 |
14 |
221,0 |
276,0 |
+1,0 |
1,2 |
1,2 |
12,0 |
10,7 |
15 |
48,5 |
110,5 |
-1,5 |
1,1 |
1,1 |
10,2 |
9,7 |
16 |
05,5 |
336,5 |
+1,5 |
0.8 |
0.8 |
13,6 |
10,7 |
17 |
58,0 |
352,0 |
-2,0 |
0.7 |
0.7 |
9,8 |
13,5 |
18 |
162,0 |
223,0 |
+2,0 |
0.6 |
0.6 |
9,2 |
7,6 |
19 |
316,0 |
258,0 |
-3,0 |
0,4 |
0,4 |
15,6 |
9,5 |
20 |
51,0 |
03,0 |
+3,0 |
0,3 |
0,3 |
17.0 |
14,2 |
№ варианта |
КП1 |
КП2 |
ΔГК |
m1 |
m2 |
D1 |
D2 |
21 |
218,0 |
78,0 |
+2,0 |
0,3 |
0,3 |
15,4 |
10,2 |
22 |
112,0 |
212,0 |
+3,0 |
0,7 |
0,7 |
9,8 |
13,5 |
23 |
47,0 |
144,0 |
-2,0 |
0,6 |
0,6 |
11,2 |
14,3 |
24 |
09,5 |
68,5 |
+1,5 |
1,1 |
1,1 |
6,7 |
10,8 |
25 |
316,0 |
56,0 |
-1,0 |
1,2 |
1,2 |
15,3 |
13,4 |
26 |
190,0 |
285,0 |
-3,0 |
1,3 |
1,3 |
10,5 |
11,6 |
27 |
211,5 |
278,5 |
-1,5 |
1,5 |
1,5 |
11,6 |
7,4 |
28 |
11,0 |
282,0 |
+4,0 |
0,2 |
0,2 |
11,2 |
9,7 |
29 |
76,5 |
201,5 |
-2,5 |
0,8 |
0,8 |
15,3 |
10,6 |
30 |
94,0 |
260,0 |
+1,0 |
0,5 |
0,5 |
9,8 |
12,4 |