7.6. Канальные алгоритмы трассировки

В настоящее время распространение получили канальные алгоритмы трассировки, основанные на прокладке трасс по укрупненным дискретам КП, в качестве которых служит система горизонтальных и вертикальных каналов. Ширина каждого канала зависит от числа прокладываемых в них соединений. Канал разбивается на линейки, называемые магистралями. Любое соединение при канальной трассировке будет представлять совокупность объединенных в одну цепь участков магистралей.

Реализация канального алгоритма предполагает выполнение двух процедур:

1. Распределение соединений по каналам с учетом их оптимальной загрузки;

2. Оптимизация расположения соединений на магистралях каналов.

Для заданной конструктивно-технологической базы каждому каналу монтажной плоскости можно поставить в соответствие число, называемое пропускной способностью канала и обозначающее максимальное допустимое число проводников, проходящих через сечение канала с выполнением технологических ограничений. При этом процедура оптимального распределения соединений по каналам в простом случае сводится к их равномерной загрузке, а в более сложных случаях, кроме того, осуществляется учет электромагнитной и тепловой совместимости соседних проводников.

Целью выполнения второй процедуры является минимизация числа переходных отверстий с одного слоя монтажной плоскости на другой.

Задачи первой процедуры решаются с помощью алгоритмов построения минимальных связывающих деревьев (МСД). В процессе построения МСД для каждого соединения учитывается загрузка каждого из каналов, через которые оно проходит.

Часто для распределения соединений по каналам вместо процедур построения МСД используются волновые процедуры, при этом дискретами для распространения волны на коммутационном поле являются каналы.

Задача распределения соединений по магистралям обычно формулируется следующим образом. Дан горизонтальный канал, ограниченный верхним и нижним рядами. Между верхним и нижним рядами заданы множества свободных линий, магистралей. Необходимо в общем случае ломаными линиями, проходящими по участкам магистралей, соединить все абсциссы одноименных групп контактов (каждая группа соответствует одной и той же цепи), затем вертикальными отрезками соединить контакты. Трассировку следует производить по выбранному критерию качества (суммарная длина, число межслойных переходов, процент реализованных соединений, количество занятых ма­гистралей и т. д.).

Первый алгоритм канальной трассировки (так называемая «классическая» постановка задачи, не допускающая излома или перехода горизонтального сегмента соединения с магистрали на магистраль) был предложен Хашимото и Стивенсом в 1971 г. (A. Hashimoto, J. Stivens). Алгоритм получил также название «алгоритм левого конца».

Пусть задано некоторое множество отрезков, распределенных в одном канале S={M₁, M₂, …, M_n}. Два отрезка считаются пересекающимися, если M_i  M_j  . Графом интервалов G(S) множества S называется граф, вершинами которого являются отрезки M_i, а ребра соответствуют пересечению M_i и M_j. Теперь задача распределения соединений по магистралям сводится к минимальной раскраске графа интервалов G(S). При этом окрашенные одним цветом отрезки помещаются на одной магистрали, а хроматическое число графа интервалов – необходимое для проведения соединений число магистралей.

Алгоритм «левого конца» является достаточно простым алгоритмом раскраски графа.

Алгоритм заключается в следующем:

1. Упорядочить отрезки по координатам левого конца;

2. Просматривая последовательность слева направо, красить вершины первой по порядку краской, которой не окрашены смежные с ней вершины.

Пример. Даны отрезки, координаты, которых получены на первом этапе. Строим граф интервалов (рис. 7.40).

Рисунок 7.40. Отрезки соединений и граф интервалов G(S)

Упорядочим отрезки по координатам левого конца: M₄, M₁, M₂, M₃, M₆, M₅

Красим вершину M₄ в первый цвет (помещаем на первую магистраль). Вершина M₁ смежна вершине M₄, красим ее во второй цвет (помещаем на вторую магистраль). Вершина M₂ смежна вершинам M₄ и M₁, красим ее в третий цвет (помещаем на третью магистраль). Вершина M₃ не смежна вершине M₄, красим ее в первый цвет (помещаем на первую магистраль). Вершина M₆ смежна вершине M₄ и не смежна вершине M₁, красим ее во второй цвет (помещаем на вторую магистраль). Вершина M₅ смежна вершинам M₃ и M₆, и не смежна вершине M₂, красим ее в третий цвет (помещаем на третью магистраль). Результаты распределения отрезков по магистралям приведены на рис. 7.41 (а).

Однако на практике недостаточно разместить проводники на горизонтальных магистралях, необходимо подсоединить их вертикальными проводниками к соответствующим выводам канала. Для этого, вводится граф вертикальных ограничений, показывающий какое соединение должно стоять выше, а какое ниже. На рис. 7.41(б) показан горизонтальный канал. Граф вертикальных ограничений для соединений этого канала приведен на рис. 7.41(в).

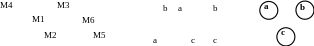
Р исунок 7.41. Распределение проводников в канале (а); горизонтальный канал (б); граф вертикальных ограничений (в)

Распределение проводников по магистралям с учетом графа вертикальных ограничений показано на рис. 7.42 (а). Распределение не оптимально. Оптимальное распределение, полученное с помощью «алгоритма правого конца», показано на рис. 7.42 (б).

а

б

Рисунок 7.42. Распределение соединений по «алгоритму левого конца» (а) и оптимальное распределение по «алгоритму правого конца» (б)

Д.Н. Дойч (D.N. Deutsch) предложил алгоритм «Dogleg» (дословно – собачья лапа, резкое искривление), разрешающий строить ломаную линию. Алгоритм состоит из двух частей:

1. Соединения упорядочиваются по левому концу с учетом графа вертикальных ограничений. Соединения проводятся на возможно верхних магистралях с разрешением изломов.

2. Начиная с правого соединения, они спрямляются с целью уменьшения числа межслойных переходов.

На рис. 7.43 (а) показаны контакты, которые необходимо соединить. На рис. 7.43 (б) приведен граф вертикальных ограничений. На рис. 7.43.(в) показан результат первого этапа алгоритма, а на рис. 7.43 (г) – окончательный результат. Удалось спрямить только соединение d – d.

Рисунок 7.43. Распределение соединений по магистралям алгоритмом «Dogleg»

Хороший результат дает модификация алгоритма «Dogleg», заключающаяся в попеременном использовании «алгоритмов левого (для верхних магистралей) и правого (для нижних) концов».

Следует отметить, что при классической постановке задачи возможно возникновение тупиковых ситуаций, обусловленных наличием циклов в графе вертикальных ограничений.

Р

a

ассмотрим пример на рис. 7.44 (а). В графе вертикальных ограничений есть цикл. Задача не может быть решена в классической постановке, поэтому необходимо применить излом горизонталь­ных сегментов с магистрали на магистраль. Обычно в таких случаях вводятся дополнительные псевдоконтакты, например а' и а" (рис. 7.44 (б) или 7.44 (в)), около которых соединение изламывается, и далее обычным образом оперируют двумя отрезками а-а' и а"-а.

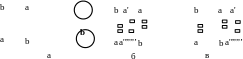
Рисунок 7.44. Обработка тупиковой ситуации алгоритмом «Dogleg»

Низкая временная и пространственная сложность алгоритмов канальной трассировки делает их наиболее приемлемыми в САПР электронных систем, где решаются задачи огромной размерности (несколько миллионов транзисторов).

Рассмотренный метод канальной трассировки успешно применим к ре­гулярным структурам печатных плат или БИС.

Достоинствами канальных алгоритмов являются:

1. Быстродействие (на один – два порядка выше, чем у волновых алгоритмов);

2. Меньший расход оперативной памяти ЭВМ (хранится не все ДРП, а только дискреты одного канала);

3. Параллельный характер работы. При распределении соединений по магистралям учитываются конфликты с другими проводниками.

Недостатком канальных алгоритмов является то, что они менее универсальны, используются только для регулярных конструкций.