7.2.2. Алгоритм, использующий упорядочивание вершин

Алгоритм состоит из следующих операций:

1. Положить j = 1;

2. В матрице R подсчитываем число ненулевых элементов r_i;

3. Упорядочим вершины графа в порядке невозрастания r_i.;

4. Просматривая последовательность слева направо, красить в цвет j каждую неокрашенную вершину, не смежную с уже окрашенными в этот цвет;

5. Если остались неокрашенные вершины, то удалить из матрицы R строки и столбцы, соответствующие окрашенным вершинам. Положить j = j + 1 и перейти к п. 2, иначе, задача решена.

Пример. Раскрасить вершины графа рис.7.20.

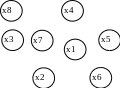
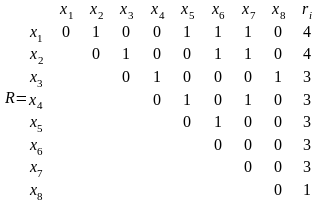
Рисунок 7.20. Исходный граф и его матрица соединений

1. Положим j = 1;

2. Упорядочим вершины графа в порядке невозрастания r_i.

x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈;

3. Красим в первый цвет вершины x₁ и x₃. Вершины x₄, и x₈ смежны вершине x₃, остальные – смежны вершине x₁;

4. Остались неокрашенные вершины, поэтому удалим из матрицы R строки и столбцы, соответствующие вершинам x₁ и x₃. Положим j = j + 1 = 2.

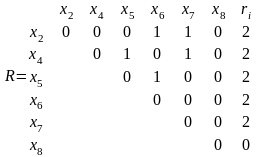
5. Упорядочим вершины графа в порядке невозрастания r_i: x₂, x₄, x₅, x₆, x₇, x₈;

6. Красим во второй цвет вершины x₂, x₄ и x₈. Вершины x₅ и x₇, смежны вершине x₄, вершина x₆ смежна вершине x₂;

7. Остались неокрашенные вершины, удалим из матрицы R строки и столбцы, соответствующие вершинам x₂, x₄ и x₈. Положим j = j + 1 = 3.

8. Упорядочим вершины графа в порядке невозрастания r_i : x₅, x₆, x_7.

9. Красим в третий цвет вершины x₅ и x₇. Вершина x₆ смежна вершине x₅;

10. Осталась неокрашенная вершина, удалим из матрицы R строки и столбцы, соответствующие вершинам x₅ и x₇. Положим j = j + 1 = 4.

11. В четвертый цвет окрашиваем вершину x₆.

Все вершины окрашены.

Достоинство алгоритма – быстродействие. Недостаток – не оптимальность.

Для раскраски вершин графа приближенным алгоритмом потребовалось четыре цвета. А хроматическое число графа (G) = 3. Действительно, если в первый цвет окрасить вершины x₁, x₄ и x₈, во второй – x₂ и x₅, то в третий можно окрасить оставшиеся вершины x₃, x₆ и x₇.

Это связано с тем, что алгоритм рассматривает только количественные характеристики вершин, и не рассматривает качественные. Так, степени вершин x₃ и x₄ одинаковые, но вершина x₃ смежна висячей вершине x₈, а вершина x₄ – сильносвязным вершинам x₅ и x₇.

С. На третьем этапе определяется последовательность проведения соединений, т. е. указывается, когда каждый проводник будет проведен.

3. Порядок проведения проводников

Трассировка цепей выполняется последовательно, и каждая проложенная трасса является препятствием для еще не проведенных. В связи с этим большое значение приобретает задача нахождения последовательности проведения соединений в каждом слое. Порядок трассировки оказывает значительное влияние на качество трассировки.

Рассмотрим пример (рис. 7.21 (а)). Необходимо соединить одноименные контакты.

Если первыми соединять контакты а, то контакты b можно соединить с небольшим обходом (рис. 7.21 (б)). Если же первыми соединять контакты b, то соединение контактов a значительно увеличит длину проводника (рис. 7.21 (в)).

Рисунок 7.21. Зависимость качества трассировки от порядка проведения проводников

Еще один пример (рис. 7.22 (а)). Задача та же. Если первыми соединять контакты b, то и контакты а легко соединяются (рис. 7.22 (б)). Если же первыми соединять контакты а, то контакты b окажутся заблокированными (рис. 7.22 (в)).

		b	а
а
	b

		b	а
а
	b

		b	а
а
	b

а б в

Рисунок 7.22. Влияние порядка проведения проводников

Идея алгоритмов определения порядка проведения соединений заключается в том, что первыми проводятся проводники, меньше «мешающие» другим проводникам.

Метод прямоугольников

1. Для всех пар контактов строятся минимальные охватывающие прямоугольники;

2. Для каждого прямоугольника подсчитывается число контактов других соединений, попавших в данный прямоугольник;

3. Соединения упорядочиваются по неубыванию этих чисел;

4. Получен порядок проведения соединений.

П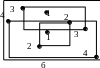 ример. Определить порядок проведения соединений (рис. 7.23 (а)).

Рисунок 7.23. Определение порядка проведения проводников

1. Строим минимальные охватывающие прямоугольники (рис. 7.23 (б));

2. Число контактов других соединений, попавших в данный прямоугольник

1 – 0; 2 – 1; 3 – 2; 4 – 4;

3. Упорядочим соединения 1, 2, 3, 4;

4. Проведем соединения в найденном порядке (рис. 7.23 (в)).

В пакетах автоматизированного проектирования заложена возможность редактирования стратегии трассировки, а именно, выбрать порядок проведения проводников (RouteOrder): Short – Long – сначала короткие, потом длинные, или Long -Short- сначала длинные, потом короткие.

Анализируя результаты работы метода, можно сделать вывод, что первыми следует проводить короткие проводники. Но в этом случае автоматически разводятся простые соединения, заполняя коммутационное пространство (согласно закону Паркинсона «Работа заполняет время, отпущенное на неё»), оставляя длинные проводники на ручную доработку. Поэтому при применении варианта Short-Long число неразведенных связей меньше, но ручная допроводка сопряжена с большими трудностями, чем при использовании варианта Long-Short. С другой стороны, если первыми проводить длинные соединения, то на заполненном коммутационном поле короткие проводники станут длинными. Лучший вариант можно выбрать, применив обе стратегии трассировки.

4. На четвертом этапе дается ответ, каким образом (каким алгоритмом) должно быть проведено каждое соединение.