6.4. Конструктивные алгоритмы начального размещения

Характерной особенностью этого класса алгоритмов является то, что они создают размещение.

Среди конструктивных алгоритмов размещения выделяют последовательные и параллельно-последовательные алгоритмы.

Наиболее представительная группа конструктивных алгоритмов – алгоритмы последовательного размещения.

Рассмотрим алгоритм последовательного размещения по связности.

Вводится n - шаговый процесс принятия решений, на каждом шаге которого выбирается один из неразмещенных элементов и помещается в одну из незанятых позиций.

Структура любого последовательного алгоритма размещения определяется правилами выбора очередного элемента и позиции для его установки.

Пусть, E_k - элементы, размещенные за k шагов алгоритма, а P_k - позиции, занятые этими элементами.

Для каждого неразмещенного элемента e_iE_k подсчитывается характеристика

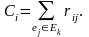
Очередным размещенным элементом является элемент, имеющий максимальную характеристику C_i, т.е. выбор элемента осуществляется по наибольшему числу связей с уже размещенными элементами.

Позиция-кандидат для установки e_i выбирается с учетом связности e_i с уже размещенными элементами.

Для каждой свободной позиции p_t вычисляется характеристика

Выбирается та из позиций, для которой F_t минимальна.

Для экономии вычислений всегда целесообразно рассматривать не все множество позиций p_tP_k , а лишь часть, находящихся на периферии множества P_k незанятых позиций.

В любом последовательном алгоритме размещения особо оговаривается правило размещения первого элемента. Первым размещается элемент, входящий в максимальное число цепей. Он помещается в центр коммутационного поля.

Достоинством последовательных алгоритмов является быстродействие.

Недостатком является последовательный характер, оптимизируется только размещение элемента-кандидата.

Для оптимизации размещения используются итерационные алгоритмы.

6.5. Алгоритм обратного размещения

Алгоритм обратного размещения принадлежит группе алгоритмов параллельно-последовательного размещения.

В методе обратного размещения осуществляются предварительные оценки каждого из размещаемых элементов и каждой свободной позиции, после чего все элементы размещаются одновременно.

Даны: матрица соединений R и матрица расстояний D.

Для каждого элемента e_i найдем суммарное число соединений с другими элементами

Для каждой позиции p_i найдем суммарное расстояние до остальных позиций

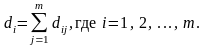
Очевидно, что позиции в центральной части коммутационного поля имеют меньшую характеристику d_i, чем позиции на периферии. Естественно, что центральные позиции наиболее благоприятны для размещения сильно связанных элементов.

Учитывая условия минимальности скалярного произведения r×d, получим следующий алгоритм:

1. Упорядочить элементы e_i в порядке неубывания r_i;

2. Упорядочить позиции p_i в порядке невозрастания d_i;

3. i-ый элемент из упорядоченного списка элементов помещается в i-ую позицию из упорядоченного списка позиций.

Достоинство алгоритма – простота. Он может быть использован даже при ручном проектировании.

Недостаток – неоптимальность размещения.

П ример. Разместить элементы, заданные взвешенным графом G (рис. 6.6 (а)) на множестве позиций Р (рис. 6.6 (б)).

Рисунок 6.6. Взвешенный граф G (а) и множество позиций Р (б)

Составим матрицы соединений R и расстояний D.

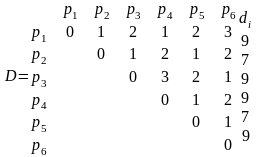
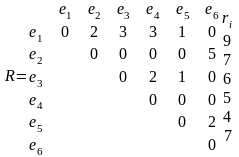
1. Упорядочим элементы e_i в порядке неубывания r_i {e₅, e₄, e₃, e₆, e₂, e₁}.

2. Упорядочим позиции p_i в порядке невозрастания d_i {p₁, p₃, p₄, p₆, p₂, p₅}.

3. Размещаем элементы в соответствии с упорядоченными списками (рис. 6.7).

Рисунок 6.7. Результат размещения

Значение целевой функции для полученного размещения F(р)=36. Низкое качество размещения объясняется, прежде всего, небольшим количеством позиций, четыре позиции из шести имеют одинаковую характеристику d_i. Но этим можно воспользоваться для улучшения размещения. Можно менять позиции вершин, помещенные в равноценные позиции. Так, можно переставить вершины e₄ и e₆ (рис. 6.8 (а)). Целевая функция нового размещения F(р)=24. У оптимального размещения (рис. 6.8 (б)) значение целевой функции F(р)=22.

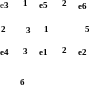
a

Рисунок 6.8. Улучшенное (а) и оптимальное (б) размещения