3.6. Математические модели электрических схем

Любая функциональная или принципиальная схема состоит из набора элементов, заданным образом соединенных между собой. Поэтому схему можно рассматривать как некоторое множество элементов E={e₁, e₂, ..., e_m}, соединенных между собой цепями из множества U={u₁, u₂, ..., u_n}. Пусть дана электрическая схема (рис. 3.24).

Рисунок 3.24. Электрическая схема

Схему можно представить в виде различных графов.

1. Модель схемы в виде двудольного графа g(e, u, p)

Модель представляет два множества E и U, вершины которых соединены между собой. Вершина e_i соединяется с цепью u_j, если она принадлежит этой цепи (рис. 3.25).

Рисунок 3.25. Двудольный граф, описывающий схему

Достоинство такой модели в том, по ней с точностью до входов/выходов можно восстановить схему, т.к. сохраняется состав цепей.

Недостатком модели является низкая наглядность. Так, по модели сложно определить связность элементов.

2. Модель схемы в виде гиперграфа h(e, u)

Гиперграфом H(E, U) называется граф, ребра которого могут соединять больше двух вершин. Ребра в гиперграфе называются гиперребрами. В модели схемы гиперребро это цепь.

На рис. 3.26 приведена модель схемы в виде гиперграфа.

Достоинства и недостатки у гиперграфа такие же, как и двудольного графа.

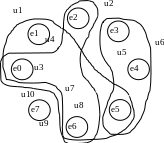
Рисунок 3.26. Гиперграф, описывающий схему

В ЭВМ двудольный граф и гиперграф представляются матрицей комплексов Q=q_ij_nk, строки которой соответствуют элементам, а столбцы – цепям, где Матрица комплексов аналогична матрице инцидентности, отличие состоит в том, что в столбце может быть больше двух единиц. Для рассматриваемой схемы матрица комплексов:

3. Модель схемы в виде мультиграфа g(e, u)

Мультиграф легко получить из двудольного графа. Необходимо, последовательно просматривая цепи, соединять между собой элементы, входящие в цепь (рис. 3.27).

Рисунок 3.27. Модель схемы в виде мультиграфа

Достоинство модели – наглядность. На графе видно, как элементы связаны между собой.

Недостатки модели следующие:

1. Цепи распались на отдельные проводники и невозможно определить, к какой цепи принадлежит конкретный проводник. Схему по модели восстановить нельзя.

2. Главный недостаток модели – неточность, избыточность. Каждая цепь представлена полным подграфом. А на практике, например, при размещении элементов будем пытаться уменьшить длину всех проводников, хотя цепь будет реализована в виде дерева.

4. Модель схемы в виде взвешенного графа G(E, U). Модель строится, как и мультиграф, только проводятся не кратные ребра, а рядом с ребрами ставится вес – кратность ребра. Свойства модели такие же, как и у мультиграфа.

В ЭВМ взвешенный граф и мультиграф представляются матрицей смежности, которая в САПР называется матрицей соединений R=r_ij_nn. Матрицу соединений легко получить из матрицы комплексов .

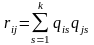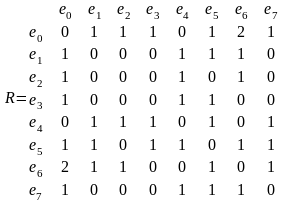
Разработан еще целый ряд моделей схемы в виде различных графов, которые с разной степенью детализации отражают свойства объекта.

Для дальнейшего рассмотрения алгоритмов конструкторского проектирования ограничимся описанными моделями.