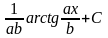Правила дифференцирования:

Пусть U и V – функции переменной x, С – постоянная величина.

_{; ;} ;

Формулы дифференцирования:
Элементарны функции:		Сложные функции:
	-
	-

- «Неопределённый интеграл» следует применять свойства неопределенного интеграла, основные формулы интегрирования и если после алгебраических преобразований нельзя применить формулы интегрирования, то необходимо воспользоваться методом подстановки, методом интегрирования по частям или методом интегрирования рациональных дробей.

Основные формулы интегрирования

=		=
=		=
=		=
=		=
=		=
=		=
=		=
=		=
=		=
=		=
=		=

- «Определённый интеграл» необходимо использовать понятие определенного интеграла, формулу Ньютона-Лейбница для его вычисления, свойства определенного интеграла и методы интегрирования.

- «Площадь криволинейной трапеции» следует применять понятие определенного интеграла и его применение при вычислении площади криволинейной трапеции, учитывая случаи расположения фигуры в системе координат.

Контрольная работа

Требования к оформлению контрольной работы

Контрольную работу следует выполнять в ученических тетрадях (желательно в клеточку). На обложке необходимо указать: название учебного заведения, название специальности, курс, номер группы, фамилию, имя, отчество и личный номер студента (который определяется по номеру в журнале группы).

На каждой странице необходимо оставить поля 4 см для оценки задач и методических указаний проверяющего работу.

Условия задач переписывать необязательно, достаточно указать номер задачи.

1. Линейная алгебра

1. Действия над матрицами

Выполнить действия:

а). ; б). .

1.2. Вычисление определителей

Проверить, что определитель Δ равен нулю:

а). Методом треугольников; б). Разложением по строке.

1.3. Обратная матрица

Найти обратную матрицу к матрице А и проверить выполнение равенства :

а). ; б). .

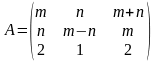1.4. Системы линейных уравнений

а). Записать систему в матричном виде и решить её с помощью вычисления обратной матрицы:

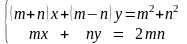
б). Решить систему методом Крамера:

2. Теория пределов

2.1. Пределы при x→n

а). ; б). .

2.2. Пределы при x→∞

а). ; б). .

2.3. Замечательные пределы

а). 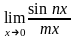; б). ; в). ; г).

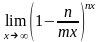
3. Приложение производной

3.1. Найти наибольшее и наименьшее значения функции 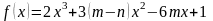на отрезке .

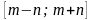3.2. Найти интервалы монотонности и точки экстремума функции .

4. Неопределённый интеграл

4.1. Найти интегралы:

5. Определённый интеграл

5.1. Построить схематически чертёж и найти площадь фигуры, ограниченной линиями:

Экзаменационные вопросы

1. Матрицы.

2. Действия над матрицами.

3. Определитель матрицы и его свойства.

4. Миноры и алгебраические дополнения элементов матриц.

5. Теорема Лапласа.

6. Ранг матрицы.

7. Обратная матрица.

8. Решение простейших матричных уравнений и систем линейных уравнений в матричной форме.

9. Решение систем линейных уравнений методом Кремера.

10. Решение систем линейных уравнений методом Гаусса.

11. Понятие функции. Основные свойства функций.

12. Предел переменной величины. Основные свойства.

13. Предел функции в точке.

14. Предел функции на бесконечности.

15. Замечательные пределы.

16. Непрерывность функции.

17. Точки разрыва. Их классификация.

18. Производная функции. Производные основных элементарных функций. Производная сложной функции.

19. Дифференциал функции. Применение дифференциала в приближённых вычислениях.

20. Интервалы возрастания и убывания функции. Экстремумы функции.

21. Наибольшее и наименьшее значения функции.

22. Выпуклость и вогнутость. Точки перегиба.

23. Асимптоты графика функции.

24. Полное исследование функции и построение её графика.

25. Первообразная функции. Неопределённый интеграл и его свойства.

26. Основные формулы интегрирования.

27. Метод подстановки. Метод интегрирования по частям.

28. Интегрирование рациональных дробей.

29. Определённый интеграл и его свойства.

30. Методы интегрирования определённого интеграла.

31. Вычисление площадей криволинейных трапеций. Вычисление объёмов тел вращения.

32. Физический смысл определённого интеграла.

Перечень рекомендуемых учебных изданий, интернет-ресурсов, дополнительной литературы

Наличие глобальной сети INTERNET

Основные источники:

1. http://e.lanbook.com/ А.С.Ащеулова, О.С. Карнадуд Высшая математика. Линейная алгебра и аналитическая геометрия. – Кемеровкий государственный университет. Кемерово, 2011.

2. http://e.lanbook.com/ С.А.Барвенов, Т.П.Бахтина Математика. – ТетраСистемс, Минск,2013.

3. http://www.iprbookshop.ru А.А.Гусак, Е.А.Бричикова, ТетраСистемс «Теория вероятностей.», 2013

Дополнительные источники:

1. Богомолов Н.В. Практические занятия по математике: Учебное пособие - М. Высшая школа, 2010;

2. Гмурман В.Е. Теория вероятностей и математической статистики. Учебное пособие – М.: Высшая школа, 2011;

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Учебное пособие – М.: Высшая школа, 2010;

4. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах Учебное пособие - М. Новая волна, 2013;

5. Лапчик М.П., Рагулина М.И., Хенкер Е.К. Элементы численных методов: учебник -М.: Издательский центр «Академия», 2013;

6. Подольский В. А. Сборник задач по математике: Учебное - М. Высшая школа, 2011;

7. Выгодский М.Я. Справочник по высшей математике. - М. Росткнига, 2013;

8. Кремер Н.Ш. Высшая математика для экономистов – учебник для вузов – М.: Юнити, 2011;

9. Щипачев В.С. Задачи по высшей математике – учебное пособие - М., Высшая школа, 2012;

10. Соловейчик И.Л., Лисичкин В.Т. Сборник задач по математике: Учебное пособие- М. Высшая школа , 2012;

11. Математика on-line: справочная информация в помощь студенту http:\\www.mathem.h1.ru;

12. Математика в помощь школьнику и студенту (тесты по математике on-line)

http:\\www.mathtest.ru.

13. www.mathelp.spb.ru/index1.htm

14. www.toehelp.ru/theory/math/

Приложение №1
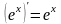
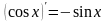
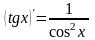
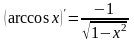
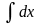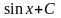
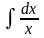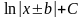
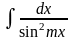
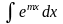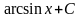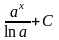
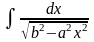
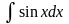
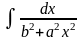