Лекция 2. Геометрические характеристики плоских сечений.

Основной объект, изучаемый в курсе сопромата – это стержень.

Сопротивление стержня различным видам деформации зависит не только от материала и его размеров, но также от формы поперечных сечений и их расположения.

К геометрическим характеристикам относятся площади поперечных сечений, статические моменты, моменты инерции, радиусы инерции.

Статический момент площади.

Рассмотрим произвольную фигуру (поперечное сечение бруса), связанную с координатными осями oz и оу.

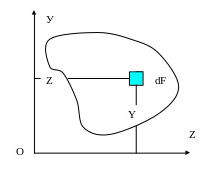
Выделим элемент площади dF с координатами z, y

По аналогии с выражением для момента силы относительно какой-либо оси, можно составить выражение момента площади, которое называется статическим моментом.

Статическим моментом элемента площади, относительно оси OZ называется произведение элемента площади dF, на расстояние У от оси OZ

Просуммировав такие произведения по всей площади фигуры, получим статические моменты относительно осей OZ и OY.

Статические моменты имеют размерность см³.

Для вычисления статических моментов сложной фигуры, ее разбивают на простые части.

Статический момент всей фигуры относительно данной оси определяется как сумма статических моментов каждой части.

Координаты центра тяжести определяются по формуле:

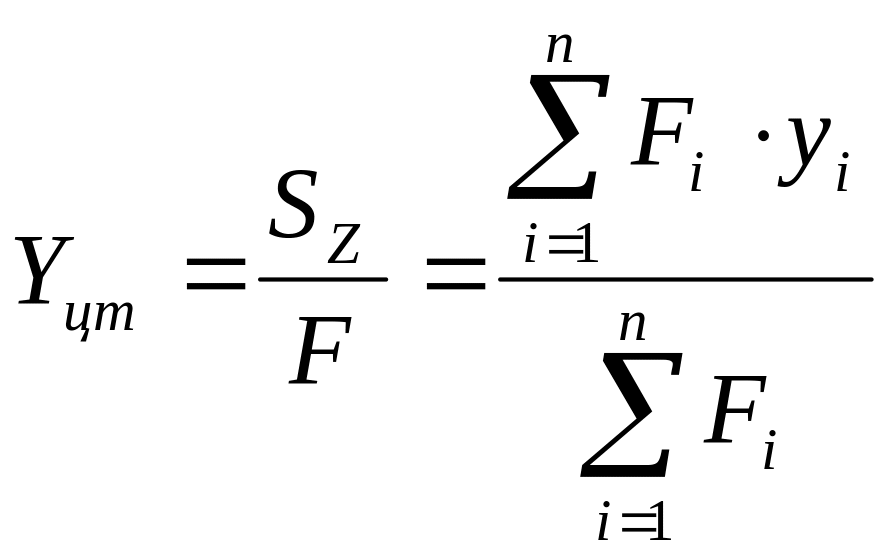
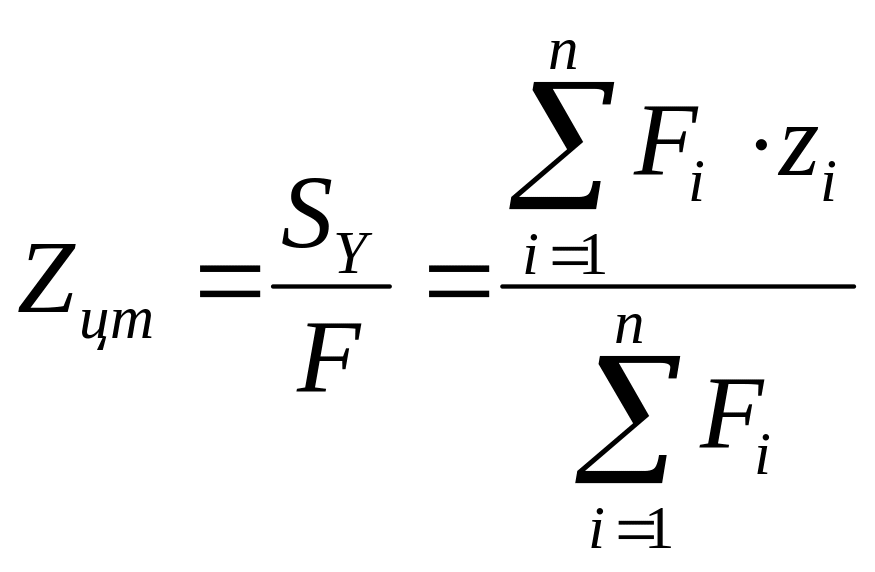
Моменты инерции плоских фигур.

Для полной геометрической характеристики сечения необходимо знать три типа моментов инерции: осевой, полярный и центробежный.

Осевым моментом инерции площади фигуры называется интеграл произведений элементарных площадок на квадраты их расстояний от данной оси.

Полярным моментом инерции площади фигуры относительно данной точки (полюса) называется интеграл произведений элементарных площадок на квадраты их расстояний от полюса.

Осевые и полярный моменты всегда положительны, их размерность – м⁴.

Центробежным моментом инерции называется интеграл произведений площадей элементарных площадок на их расстояния от координатных осей Z и Y.

Центробежный момент инерции в зависимости от положения осей может быть положительным, отрицательным и равным нулю.

Оси, проходящие через центр тяжести, называются главными центральными осями. В теории изгиба и сложного сопротивления наибольшее значение имеют именно главные центральные оси.

Моменты инерции сложных сечений.

При вычислении моментов инерции сложных сечений следует разбить их на простые части , моменты инерции которых известны. Момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

Формулы перехода для моментов инерции при параллельном переносе осей.

а – расстояние между осями Z и Z1; в – расстояние между осями У и У1

Осевой момент инерции фигуры относительно любой оси параллельной центральной равен осевому моменту инерции плюс произведение квадрата расстояния между осями на площадь фигуры.

Центробежный момент инерции фигуры относительно любой системы прямоугольных осей параллельной центральной равен центробежному моменту инерции плюс произведение расстояний между осями на площадь фигуры.