Лекция № 10

3.2.2. Метод неявного перебора по векторной решетке (мнпвр)

Векторной решеткой называют математическую структуру, определяющую расположение и взаимосвязь различных значений n-мерного вектора x=(x[1],…,x[n]), каждая j-а компонента которого может принимать целочисленные значения, в диапазоне - . Отдельные точки вектора x располагаются по уровням Хэмминга, определяемым с использованием понятия расстояния Хэмминга.

Расстоянием Хэмминга между двумя n-мерными векторами и называют величину

(3.32)

Уровнем Хэмминга будем называть расстояние Хэмминга рассматриваемой точки от . В большинстве задач все . В этом случае нулевая точка располагается на нулевом уровне, точки (1,0,...,0), (0,1,0,...,0),...,(0,...,0,1) - на первом уровне и т.д.

Формирование векторной решетки завершает правило, согласно которому каждые две ее точки, находящиеся на соседних уровнях и отстоящие друг относительно друга на расстоянии Хэмминга, равном единице, соединяются дугой.

Наглядное графическое изображение векторной решетки для комбинаторной задачи (ограничения на оптимизационные переменные сверху h[j]=1 (j=1,2,3)) в случае n = 3 приведено на рис.3.4.

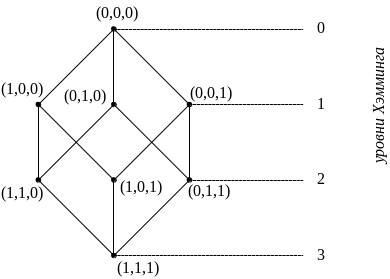
Рис.3.4

Процедура перебора.

Перебор точек векторной решетки осуществляется по ее маршрутам с помощью шагов вперед и назад.

Маршрутом называется любой путь, проходящий через вершины векторной решетки, соединенные дугами.

Шаг вперед - это переход из рассматриваемой точки на уровень с большим номером по имеющемуся в векторной решетке маршруту,

а шаг назад - обратное движение.

Так как каждый шаг вперед связан с увеличением соответствующей переменной на единицу, то будем говорить "шаг вперед по j -й переменной". Чтобы при движении вперед исключить повторное рассмотрение точек, вводится правило, согласно которому из любой точки x: рассматриваются шаги вперед лишь по тем переменным, номера которых удовлетворяют следующим условиям:

, (3.35)

где . (3.36)

Пример:

j= 1 2 3 4

h[j]= 2 3 1 5

x= 0 0 0 0 =0 {1,2,3,4}

x= 1 0 0 0 =1 {1,2,3,4}

x= 1 3 0 0 =2 {3,4}

В соответствии с этим правилом для формирования маршрутов перебора по векторной решетке, изображенной на рис.3.4, используются лишь ее дуги, показанные на рис.3.5.

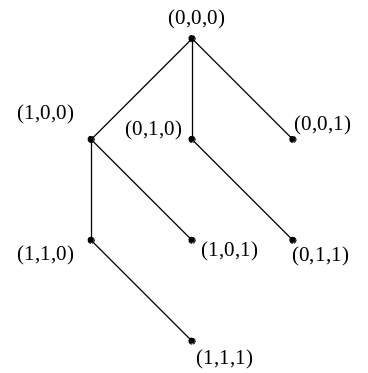
Рис.3.5

Точки, для которых =Æ, будем называть конечными. После перемещения в такую точку с помощью шага вперед обязательно будет следовать шаг назад.

Движение по векторной решетке начинается и заканчивается в нулевой точке.

Завершение перебора происходит в нулевой точке тогда, когда все шаги вперед из нее уже рассмотрены.

Преобразование оптимизационной задачи для применения мнпвр

Рассмотрим применение метода неявного перебора по векторной решетке к линейным целочисленным задачам следующего вида:

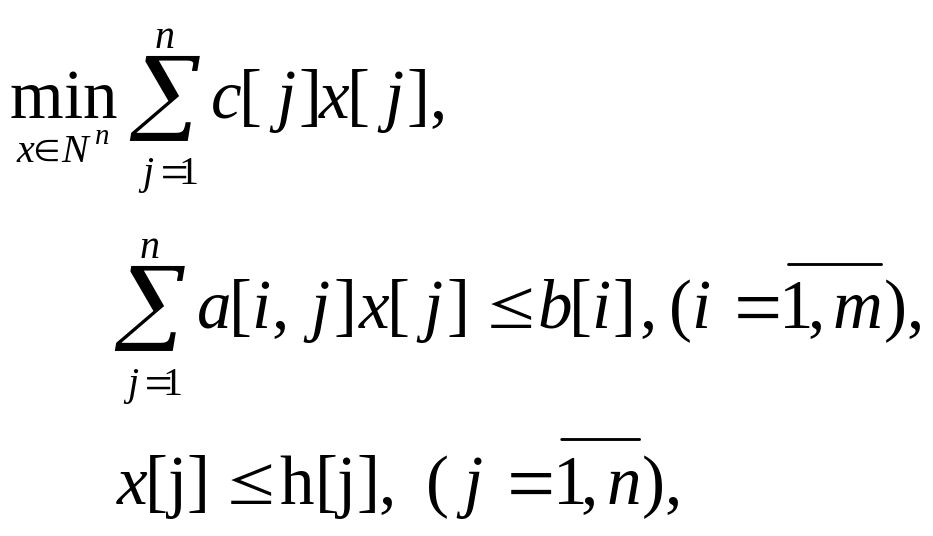(3.33)

которая приведена к виду, где все c[j]³0, а ограничения представляют неравенства типа «£».

Эти условия не являются ограничительными, так как их выполнение всегда может быть обеспечено путем соответствующих преобразований.

Если в задаче, приведенной к направлению оптимизации на минимум, коэффициент в целевой функции при j-й переменной отрицательный, то необходимо ввести замену переменных:

. (3.34)

Очевидно, что эту замену для обеспечения эквивалентности преобразования необходимо сделать не только в целевой функции, но и во всех ограничениях. После такой замены , а образовавшуюся в целевой функции константу необходимо удалить (она на результаты оптимизации не влияет).

Формальным способом преобразования ограничений типа «=» к неравенствам является замена каждого из них двумя соответствующими неравенствами противоположного знака.

Правила и критерии для сокращения перебора

Теперь рассмотрим правила, применение которых позволит сократить число перебираемых алгоритмом решений (точек) и, следовательно, сделать перебор неявным.

Правило допустимой точки.

Метод неявного перебора по векторной решетке осуществляет перебор в основном недопустимых точек: как только при движении вперед достигнута допустимая точка, это движение прекращается и делается шаг назад.

Обоснование этого правила заключается в преобразовании задачи к виду, где все c[j] ³0, а направление оптимизации - минимум. При этом движение вперед не может приводить к уменьшению целевой функции, а, как правило (при шаге вперед по переменной, для которой c[j] >0), приводит к ее увеличению, то есть к ухудшению в смысле направления оптимизации на минимум.

Как частный случай из этого правила следует вывод: если нулевая точка допустимая, то она является оптимальным решением задачи.