Вариант 13

1. Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них, за время наблюдений, может быть обнаружен или не обнаружен. Рассматриваются события: А – обнаружен ровно один из четырех объектов; В – обнаружен хотя бы один объект: С – обнаружено не менее двух объектов; D – обнаружены все четыре объекта. В чем состоят события: а) , б) 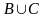, в) ВС, г) совпадают ли события BD иС?

2. Из урны, содержащей три белых, два черных и пять красных шаров, наудачу без возвращения извлекают три шара. Найти вероятность обнаружить среди них один черный и два белых.

3. Прибор может работать в двух режимах: нормальном и форсированном. Нормальный режим наблюдается в 90% случаев работы приборов. Вероятность выхода прибора из строя при нормальном режиме равна 0,08, а при форсированном - 0,8. Во время работы прибор вышел из строя. В каком режиме это вероятнее всего случилось?

4. В розыгрыше первенства по футболу участвует 18 команд, из которых случайным образом формируются две группы по 9 команд. Среди участников соревнований имеется 5 команд экстра класса. Найти вероятность того, что все команды экстра класса попадут в одну и ту же группу.

5. Стрелок ведет стрельбу до первого попадания, имея боезапас 4 патрона. Вероятность попадания при каждом выстреле равна 0,6. Составить закон распределения числа израсходованных патронов. Найти М(Х), D(X), σ(X) и F(X), где Х -число израсходованных патронов.

6. Дана функция распределения случайной величины Х. Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .

7. Дана плотность распределения непрерывной случайной величины Х. Найти: а) параметр а; б) функцию распределения F(X).

Вариант 14

1. По мишени производится три выстрела. Рассматриваются события А_i – попадание при i-м выстреле (i= 1, 2, 3). В алгебре событий выразить следующие события: А – все три промаха; В – хотя бы одно попадание; С – не меньше двух попаданий; Д – попадание в мишень не раньше, чем в третьем выстреле.

2. Буквенный замок содержит на общей оси 4 диска, каждый из которых разделен на 5 секторов, отмеченных идущими подряд натуральными числами. Замок открывается только в том случае, когда цифры образуют соответствующую комбинацию. Найти вероятность открыть замок, установив произвольную комбинацию цифр. Какова вероятность открыть замок, если известно, что кодовая комбинация содержит цифры 1, 2, 3, 5 и цифры не повторяются?

3. Вор знает, что квартира оборудована одним из трех типов сигнализации. Они срабатывают с вероятностью 0,5, 0,8, 0,9. Какова вероятность того, что при взломе сигнализация сработает, если вероятности того, что квартира оборудована i-м типом сигнализации, равны.

4. В скачках участвуют три лошади. Первая лошадь приходит первой с вероятностью 0,6, вторая – с вероятностью 0,4, а третья – 0,5. 30% зрителей на ипподроме ставят на первую лошадь, 18% - на вторую, остальные – на третью. Ваш случайный знакомый выиграл. На какую лошадь он вероятнее всего делал ставку?

5. Монета бросается 5 раз. Составить закон распределения числа появлений гербов. Найти М(Х), D(X), σ(X) и F(X) числа появлений гербов.

6. Дана функция распределения случайной величины Х.

Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .

7. Дана плотность распределения

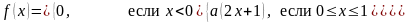
непрерывной случайной величины Х. Найти: а) параметр а; б) функцию распределения F(X).