- •Теория вероятностей и математическая статистика
- •Нижневартовск
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Дана функция распределения f(х) случайной величины х.
- •Образец выполнения задания
Вариант 25
Производится наблюдение за группой, состоящей из 5-ти однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события: А – обнаружен ровно один из 5-ти объектов; В – обнаружен хотя бы один объект; С – обнаружено не менее двух объектов; Д – обнаружено ровно два объекта; Н – обнаружены все пять объектов. В чем состоят события: а) АВ; б)D
 H;
в) ВН? Совпадают ли события ВС и D?
H;
в) ВН? Совпадают ли события ВС и D?
Найти вероятность того, что четырехзначный номер случайно встретившейся автомашины: а) не содержит одинаковых цифр; б) содержит цифру 1.
Выход из строя за время t элементов электрической цепи – независимые события, имеющие соответственно следующие вероятности: Р
 =0,3;
Р
=0,3;
Р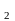 =0,33;
Р
=0,33;
Р =0,35;
Р
=0,35;
Р =0,4.
Определить вероятность разрыва цепи
за указанный промежуток времени.
=0,4.
Определить вероятность разрыва цепи
за указанный промежуток времени.В тире имеются 3 ружья, вероятности попадания из которых равны соответственно 0,7; 0,8; 0,9. Стрелок взял одно из них наудачу и при одном выстреле поразил мишень. Какова вероятность, что он стрелял из первого ружья?
Вероятность производства нестандартной детали равна 0,1. Из партии контролер берет деталь и проверяет ее на качество. Если она оказывается нестандартной, дальнейшие испытания прекращаются, а партия задерживается. Если деталь окажется стандартной, то контролер берет следующую и т.д. Но всего он проверяет не более 3-х деталей. Найти M(X); D(X);
 (Х)
и F(Х)
этой случайной величины.
(Х)
и F(Х)
этой случайной величины.
Дана функция распределения f(х) случайной величины х.
F(x)
=

Найти:
а) плотность распределения f
(Х);
б) построить графики функций F(Х)
и f
(Х);
в) M(X);
г) D(X);
д)
(Х);
е) P
(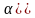 X
X ).
).
Дана плотность распределения f (x) непрерывной случайной величины Х.

Найти: а) параметр а; б) функцию распределения F(Х).
Образец выполнения задания
Задача 1. Производится наблюдение за группой, состоящей из 3-х однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события: А – обнаружен ровно один из 3-х объектов; В – обнаружен хотя бы один объект; С – обнаружено не менее двух объектов; Д - обнаружено ровно два объекта; Н – обнаружены все 3 объекта. В чем состоят события: а) АВ; б) ; в) ВН; г) ВС?
Решение. а) Событие АВ означает, что одновременно выполняются события А и В, т.е. события: «обнаружен ровно один из 3-х объектов» и «обнаружен хотя бы один объект». Следовательно, событие АВ = А и означает, что «обнаружен ровно один из 3-х объектов».
б) Событие означает, что «обнаружено ровно два объекта или обнаружены все 3 объекта».
в) ВН – одновременно выполняются события В и Н, т.е. события: «обнаружен хотя бы один объект» и «обнаружены все 3 объекта». Следовательно, событие ВН = Н и означает, что «обнаружены все 3 объекта».
г) Событие ВС означает, что выполняются одновременно события В и С, т.е. события: «обнаружен хотя бы один объект» и «обнаружено не менее двух объектов». Следовательно, событие ВС = Д и означает, что «обнаружено ровно два объекта».
Задача 2. Найти вероятность того, что четырехзначный номер случайно встретившейся автомашины: а) не содержит одинаковых цифр; б) не содержит цифру 2.
Решение. а) Пусть событиеА заключается в том, что «четырехзначный номер случайно встретившейся автомашины не содержит одинаковых цифр». Вероятность этого события найдём по формуле классической вероятности:
 ,
,
где m – число благоприятных дляА исходов, n– число всех исходов.
Найдём число m – количество четырехзначных номеров, не содержащих одинаковых цифр.
На первом месте четырехзначного номера может стоять любая цифра из десяти (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), кроме 0. Следовательно, имеем 9 вариантов того, какая цифра является первой в автомобильном номере. На втором месте может находиться любая цифра, кроме той, которая уже стоит на первом месте, т.е. тоже 9 вариантов (0 на втором месте стоять может!). На третьем месте может быть любая из 8-ми оставшихся цифр (кроме двух уже находящихся на первых местах), т.е. 8 вариантов. Соответственно, на четвёртом месте может быть любая из 7 цифр, кроме тех, которые уже заняты на первых трёх позициях.
Таким
образом,
 = 4536.
= 4536.
Найдём
число n
– количество всех четырехзначных
номеров. На первом месте четырехзначного
номера может стоять любая из 9-ти цифр
(0 не может быть на первом месте). На 2-й,
3-й и 4-й позициях может находиться любая
цифра из 10-ти существующих. Следовательно,
 .
.
По формуле классической вероятности:
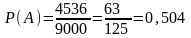 .
.
б) Пусть событиеВ заключается в том, что «четырехзначный номер случайно встретившейся автомашины не содержит цифру 2».
По формуле классической вероятности:
 .
.
Ответ. а) 0,504; б) 0,648.
Задача 3. В тире имеются 3 ружья, вероятности попадания из которых соответственно равны 0,75, 0,8, 0,9. Стрелок взял одно из них наудачу и с первого раза поразил мишень. Какова вероятность того, что он стрелял из третьего ружья?
Решение.
Пусть событиеА
заключается в том, что «стрелок с первого
раза поразил мишень», событие
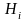 -
«стрелок выстрелил из i-го
ружья», i
= 1, 2, 3.
-
«стрелок выстрелил из i-го
ружья», i
= 1, 2, 3.
По
формуле классической вероятности:
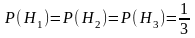 .
.
 -
вероятность попадания из 1-го ружья;
-
вероятность попадания из 1-го ружья;
 -
вероятность попадания из 2-го ружья;
-
вероятность попадания из 2-го ружья;
 -
вероятность попадания из 3-го ружья.
-
вероятность попадания из 3-го ружья.
Вероятность с первого раза поразить мишень по формуле полной вероятности равна:
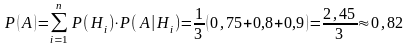
Вероятность того, что стрелок стрелял из третьего ружья, найдём по формуле Байеса:
 ,
,

 .
.
Ответ. 0,37.
Задача 4. Известно, что для одной футбольной команды вероятность выиграть 3 матча из 5, и 2 матча из 4 равны 0,6. Найти вероятность выигрыша в одном матче.
Решение. Пусть событие А заключается в том, что «футбольная команда выиграла в матче»; Р(А) = p - вероятность выигрыша в одном матче.
Вероятность
выигрыша k
раз из nматчей
можно найти по формуле
Бернулли:
 ,
где q
= 1 – p.
,
где q
= 1 – p.
Вероятность выиграть 3 матча из 5:
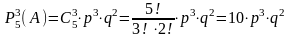
Вероятность выиграть 2 матча из 4

Поскольку эти вероятности равны друг другу и равны 0,6, то
 =
=
 =
0,6.
=
0,6.
Откуда p = 0,6.
Ответ. 0,6.
Задача 5. Подбрасывается два раза монета. Случайная величина Х - число «гербов», выпавших в двух бросаниях монеты. Составить закон распределения случайной величины Х. Найти М(Х), D(X), σ(X) и F(X).
Решение. 1) Условия данной задачи удовлетворяют всем условиям схемы Бернулли. Вероятность того, что «герб» выпадет в одном бросании монеты, p = 0,5. Тогда q = 0,5.
Возможные
значения случайной величины Х:
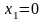 ,
,
 ,
,
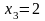 .
.
Вероятности этих значений найдём по формуле Бернулли:
, где q = 1 – p.
 ;
;
 =
=
 ;
;

 .
.
Тогда таблица распределения случайной величины Х имеет вид:
-
Х
0
1
2
p
0,25
0,5
0,25
2)
Случайная величина Х
– дискретная, поэтому её математическое
ожидание М(Х)
найдём по формуле: М(Х)
=
 ,
откуда
,
откуда
М(Х)
=
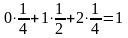 .
.
3) Дисперсию D(X) случайной величины Х найдём по формуле:
D(X)
=
 ,
,
откуда
D(X)
=
 .
.
4)
Среднеквадратическое отклонение
 .
.
5)
Найдём функцию распределения F(X)
=
 .
.
Если
 ,
то F(X)
=
= 0.
,
то F(X)
=
= 0.
Если
 ,
то F(X)
=
,
то F(X)
=
 =
0,25.
=
0,25.
Если
 ,
то F(X)
=
,
то F(X)
=
 =
0,75.
=
0,75.
Если
 ,
то F(X)
=
,
то F(X)
=
 =
1.
=
1.
Таким образом, функция распределения F(X) имеет вид:

Задача 6. Дана функция распределения случайной величины Х.

Найти:
а) плотность распределения f(X);
б) построить графики функций F(X)
и f(X);
в) М(Х);
г) D(X);
д) σ(X);
е) .
.
Решение. а) Плотность распределенияf(X) непрерывной случайной величины Х – это первая производная от функции распределения F(X):
 .
.
Поэтому
=

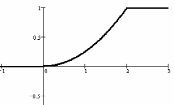
б) Построим графики функций F(X) (рис. 8) и f(X) (рис. 9).
Рис. 8. График функции F(X)
|
Рис. 9. График функции f(X) |
в) Математическое ожидание М(Х) непрерывной случайной величины Х определяется равенством
 ,
,
где f(X) - плотность распределения случайной величины Х.
Поэтому
 .
.
г) Дисперсия D(X) непрерывной случайной величины Х определяется равенством
 ,
,
где f(X) - плотность распределения случайной величины Х.
Поэтому
 .
.
д)
Среднеквадратическое отклонение
 .
.
е) Вероятность того, что непрерывная случайная величина Х принимает значение, принадлежащее интервалу (a, b), определяется равенством
 .
.
Поэтому
= .
.
Задача 7. Дана плотность распределения случайной величины Х:

Найдите: а) параметр а; б) функцию распределения F(X).
Решение.
а) Для плотности распределения случайной
величины Х
выполняется следующее свойство:
 .
Откуда
.
Откуда

 .
.
б) Найдём функцию распределения F(X) = .
Если
 ,
то F(X)
=
= 0.
,
то F(X)
=
= 0.
Если
 ,
то F(X)
=
,
то F(X)
=


=
 .
.
Если
 ,
то F(X)
= 1.
,
то F(X)
= 1.
Таким образом, функция распределения F(X) имеет вид:

Список литературы
Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е.Гмурман. – 9-е изд., стер.- М.: Высшая школа, 2009.-479с.
Горлач, Б.А. Теория вероятностей и математическая статистика: учеб.пособие / Б.А. Горлач.- СПб.: Лань, 2013.- 320с.
Туганбаев, А.А. Теория вероятностей и математическая статистика: учеб.пособие / А.А. Туганбаев, В.Г. Крупин.- СПб.: Лань, 2011.- 224с.
Гмурман, В.Е. Руководство к решению задач по теории вероятности и математической статистике: учебное пособие / В.Е. Гмурман. -7-е изд.. доп. – М.: Высшая школа, 2001
Бочаров, П.П. Теория вероятностей. Математическая статистика : учеб.пособие / П.П. Бочаров.- 2-е изд. – М.: Физматлит, 2005.-296с.
Практикум и индивидуальные задания по курсу теории вероятностей (типовые расчеты: учебное пособие / В.А.Болотюк и др.-СПб.: Лань, 2010.- 288 с.