|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ, ФИЛИАЛ В Г.НИЖНЕВАРТОВСКЕ КАФЕДРА «ИНФОРМАТИКА» |
|
Теория вероятностей и математическая статистика
Контрольные задания и методические указания к выполнению
РГР для направления подготовки «Информатика и вычислительная техника» очной и заочной формы обучения
Нижневартовск
2016
УДК
© Коледин В.В.
Одобрено
редакционно-издательским советом филиала
(протокол № 2 от 03.11.2016)
Теория вероятностей: Контрольные задания и методические указания к выполнению РГР для направления подготовки «Информатика и вычислительная техника» очной и заочной формы обучения / В.В. Коледин. – Нижневартовск, 2016. –34 с.
Задания составлены в соответствиис ФГОС-3+ по направлениям обучения «Информатика и вычислительная техника» и способствует формированиям компетенций по данным направлениям.
Утверждено на заседании кафедры
Протокол №2
«3» ноября 2016 год
Вариант 1
Эксперимент состоит в стрельбе по мишени два раза. СобытиеА – попадание в мишень первым выстрелом; событие В – попадание в мишень вторым выстрелом. Постройте множество элементарных исходов и выявите состав подмножеств, соответствующих событиям: а)
;
б) А В;
в)
.Телефонный номер состоит из 7 цифр. Найти вероятность того, что: а) все цифры номера различны; б) в номере нет цифр 1, 2, 5, 8.
К кладу ведут три дороги. Вероятность погибнуть на первой дороге равна 0,4; на второй – 0,7; на третьей – 0,8. Найти вероятность того, что ковбой доберется до клада, при условии, что дорога выбирается наудачу.
В первом ящике 3 стандартных и 1 нестандартная деталь, во втором – 1 стандартная и 3 нестандартных детали, в третьем – 3 нестандартных детали, стандартных деталей нет. Из наугад выбранного ящика взята одна деталь, которая оказалась нестандартной. Вероятней всего, из какого ящика она извлечена?
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение и функцию распределения числа отказавших элементов в одном опыте.
Дана функция распределения F(Х) случайной величины Х
Найти:
а) плотность распределения f(Х);
б) построить графики F(Х),
f(Х);
в) математическое ожидание; г) дисперсию;
д) среднеквадратическое отклонение; е)
вероятность попадания случайной величины
на интервал от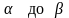
.
Задана плотность распределения f(Х) =
непрерывной случайной величины Х. Найти: а) параметр а; б) функцию распределения F(Х).
Вариант 2
Эксперимент состоит в бросании игральной кости. Пусть событиеА- появление больше четырех очков; событие В – появление больше, чем 3 очков и меньше, чем 6 очков; событие С - появление больше, чем 3 очков. Постройте множество элементарных исходов и выявите состав подмножеств, соответствующих событиям: а) ; б)
;
в)
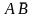.Телефонный номер состоит из шести цифр. Найти вероятность угадать номер телефона, если известно, что среди его цифр нет 0, 5, 9?
Три оператора радиолокационной установки производят, соответственно 25%, 35%, 40% всех измерений, допуская ошибку с вероятностями 0,01; 0,03; 0,02 соответственно. Случайно проведенное измерение оказалось ошибочным. Вероятнее всего, какой оператор сделал это измерение?
Вероятность попадания в мишень 0,3. Какова вероятность того, что при 30 выстрелах произойдет: а) 8 попаданий; б) не больше половины.
Вероятность промышленного содержания металла равна 0,02. Подлежит исследованию 10 проб руды. Найти закон распределения числа проб с промышленным содержанием металла. Найти М(Х), D(X), σ(X) и F(X), где X – число проб с промышленным содержанием металла.
Дана функция распределения F(X) случайной величины X. Найти: а) плотность распределения f(X); б) построить графики функций F(X) и f(X); в) М(Х); г) D(X); д) σ(X); е)
.
Дана плотность распределения f(X) =
непрерывной случайной величины Х. Найти: а) параметр а; б) функцию распределения F(X).