23

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

УЛЬЯНОВСКОЕ ВЫСШЕЕ АВИАЦИОННОЕ УЧИЛИЩЕ ГРАЖДАНСКОЙ АВИАЦИИ (ИНСТИТУТ)

Кафедра естественно - научных дисциплин

ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ

Расчетно-графическая работа

2-е издание, исправленное и дополненное

Ульяновск 2009

Исследование функций с помощью производных. Расчетно-графическая работа./ Сост. Бутузова Е.А., Лебедев А.М.

Содержит теоретические вопросы и расчетные задания по разделу математического анализа «Исследование функций с помощью производных». Предлагаемые расчетные задания составлены в соответствии с программой раздела курса высшей математики, содержат краткие теоретические сведения, контрольные вопросы и расчетные задачи. Приведены решения типовых задач с подробными объяснениями.

Настоящая работа рассмотрена методическим советом УВАУ ГА, одобрена и рекомендована в качестве учебного пособия для курсантов высшего авиационного училища гражданской авиации при изучении указанного раздела и самостоятельной подготовке.

Введение.

Важным фактором изучения курса высшей математики и практического овладения ее методами является самостоятельная работа курсанта. Типовые расчеты по разделу математического анализа «Исследование функции с помощью производных» предназначены для развития и активизации самостоятельной работы курсантов по указанной теме.

Каждый типовой расчет содержит краткие теоретические сведения, контрольные вопросы и расчетные задания. Контрольные вопросы – для всех курсантов учебной группы, а расчетные задания предлагаются индивидуально для каждого курсанта и выдаются по вариантам.

В типовых расчетах принята следующая нумерация: первое число означает номер задания, а второе – номер варианта.

Ответы на контрольные вопросы курсант готовит устно, а расчетные задания выполняются каждым курсантом письменно по мере изучения материала на лекциях и практических занятиях.

Завершающим этапом является защита типового расчета. Во время защиты курсант должен уметь правильно отвечать на контрольные вопросы, объяснять решения расчетных заданий, решать задачи аналогичного типа.

Теоретические сведения.

Функция называется возрастающей (убывающей) на некотором интервале (отрезке) , если для любых точек и , принадлежащих данному интервалу (отрезку), из неравенства , следует неравенство .

Признаки возрастания и убывания функции:

1. Если 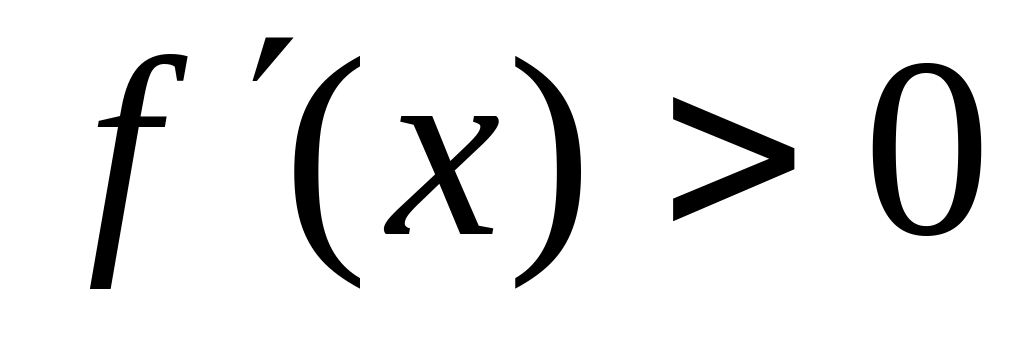на отрезке 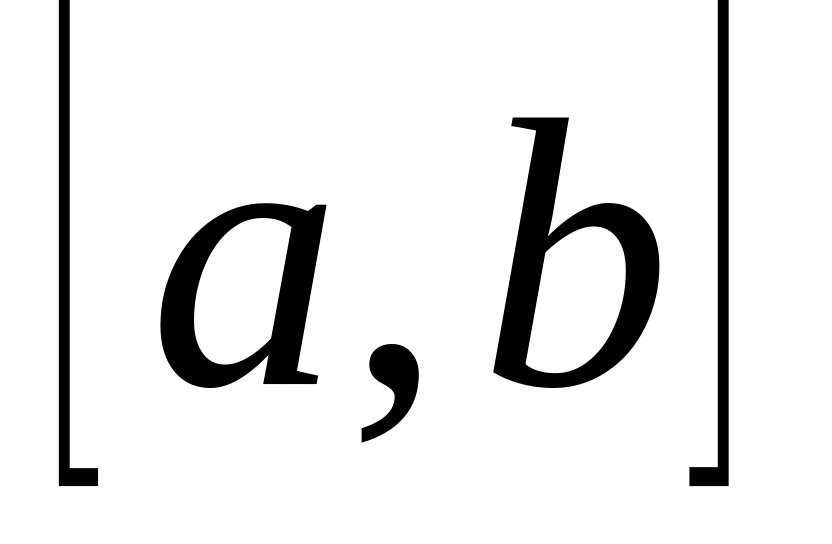, то функция 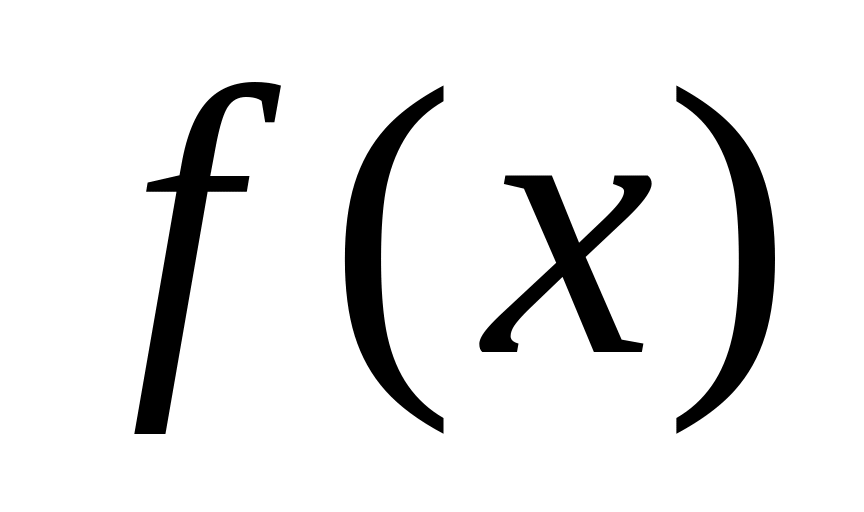возрастает на отрезке ;

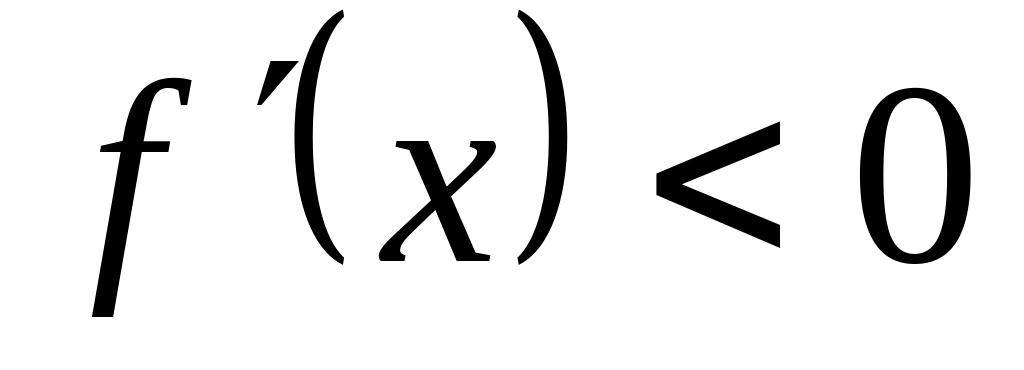2. Если на отрезке , то функция убывает на отрезке .

Точка называется точкой максимума функции , если существует такая окрестность точки , что для всякой точки этой окрестности имеет место неравенство . Число называется максимумом функции .

Точка называется точкой минимума функции , если существует такая окрестность точки , что для всякой точки этой окрестности имеет место неравенство . Число называется минимумом функции .

Максимумы и минимумы функции называются экстремумами функции. Точки, в которых функция достигает максимума или минимума, называются точками экстремума.

Необходимое условие экстремума. Если функция в точке имеет экстремум, то производная обращается в ноль в точке или не существует.

Критические точки функции , это те точки ее области определения, в которых или не существует.

Не всякая критическая точка является точкой экстремума.

Достаточное условие существования экстремума. Пусть - критическая точка и функция непрерывна в этой точке. Если в некоторой окрестности точки производная меняет знак при переходе через точку , то - точка экстремума.

При этом, если

то - точка максимума;

если

то - точка минимума.

Достаточное условие экстремума через значения второй производной. Если , то функция в точке имеет максимум, если , и минимум, если .

Для нахождения наибольшего (наименьшего) значения функции на отрезке нужно из значений функции на границах отрезка и в критических точках, принадлежащих этому отрезку, выбрать наибольшее (наименьшее).

График функции называется выпуклым на интервале , если при дуга кривой расположена ниже касательной к кривой, проведенной в любой точке интервала .

Если функция во всех точках интервала имеет отрицательную вторую производную, т.е. , то график функции выпуклый на этом интервале.

График функции называется вогнутым на интервале , если при дуга кривой расположена выше касательной к кривой, проведенной в любой точке интервала .

Если функция во всех точках интервала имеет положительную вторую производную, т.е. , то график функции вогнутый на этом интервале.

Прямая называется асимптотой для кривой при (или при ), если

(или соответственно при ).

Прямая является вертикальной асимптотой кривой , если или .

Прямая является горизонтальной асимптотой кривой , если или .

Если существуют пределы _{, ,}

то прямая _{будет наклонной асимптотой кривой .}

Или если существуют пределы _{, ,}

то прямая _{- наклонная асимптота кривой .}