1.5 Метод вращения

Метод вращения, как и метод Гаусса состоит из прямого и обратного ходов.

Прямой ход метода. Исключаем неизвестное из всех уравнений, кроме первого. Для исключения из 2-го уравнения вычисляют числа

, ,

где  и  такие, что , .

Первое уравнение системы заменяем линейной комбинацией первого и второго уравнений с коэффициентами и ,а второе уравнение такой же комбинацией с и - . В результате получим систему

. (17)

Здесь

где j= .

Преобразование системы (1) к системе (17) эквивалентно умножению матрицы A и вектора B слева на матрицу С₁₂ вида

.

Аналогично для исключения из третьего уравнения вычисляем числа

и ,

такие, что .

Затем первое уравнение системы (17) заменяем линейной комбинацией первого и третьего уравнений с коэффициентами , , а третье уравнение системы (17) тоже заменяем линейной комбинацией с ,– . Это преобразование эквивалентно умножению слева на матрицу

.

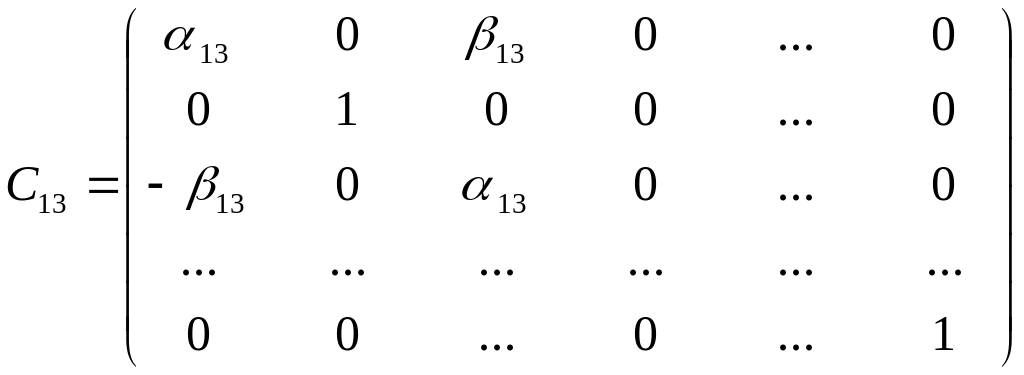Исключая неизвестное х₁ из всех последующих уравнений получим систему

А⁽¹⁾ х=В,

где матрица A⁽¹⁾=C_1m…C₁₃C₁₂A, , а вектор правых частей .

Здесь и далее через С_kj обозначена матрица элементарного преобразования, отличающаяся от единичной матрицы Е только четырьмя элементами. Действие матрицы С_kj на вектор x эквивалентно повороту вектора x вокруг оси перпендикулярной плоскости на угол такой, что

, .

Операцию умножения на матрицу С_kj называют плоским вращением или преобразованием Гивенса.

Первый этап состоит из m-1 шагов, в результате чего получается система

(18)

В матричной форме А⁽¹⁾ х=В⁽¹⁾.

На втором этапе, состоящем из m-2 шагов, из уравнений системы (2.7) с номерами 3,4,…,m исключают неизвестное х₂. B результате получим систему

В матричной форме получаем , где , .

После завершения (m-1)-го шага придем к системе с верхней треугольной матрицей вида

,

где .

Обратный ход метода вращения проводится точно также как и для метода Гаусса.

1.6 Метод отражения

Метод отражения основан на преобразованиях Хаусхолдера. Алгоритм Хаусхолдера приводит nn симметричную матрицу к трехдиагональной форме, за n–2 ортогональных преобразований. Каждое преобразование обнуляет необходимые части выбранного столбца и соответствующей строки. В этом методе QR-разложение матрицы A системы уравнений Ax = b

производится при помощи матриц отражения, которые имеют вид

U = E − 2ww^T .

Здесь E – единичная матрица; w – n-мерный вектор единичной длины, (w,w) = 1, а ww^T – квадратная симметричная матрица:

.

Следовательно, и матрица отражения U является симметричной, U =U^T. Более того, матрица U ортогональна, то есть U^T =U −1 , действительно:

UU^T = (E − 2ww^T )(E − 2ww^T )^T = E − 2ww^T − 2ww^T + 4ww^T ww^T = E ,

поскольку w^Tw = (w,w) = 1.

Так как U симметрична и ортогональна, U² =UU^T = E , собственные числа матрицы U удовлетворяют условию , то есть , причем отрицательному собственному значению λ = −1 соответствует собственный вектор w:

Uw = λw = Ew − 2ww^T w = w − 2w = −w = (−1)w → λ = −1.

Положительному собственному значению λ = 1 соответствуют все векторы, ортогональные вектору w. Если произвольный вектор v ортогонален вектору w, то есть (v,w) = 0, то

Uv = Ev − 2ww^T v = v − 2w(w,v) = v .

Рассмотрим действие матрицы U на произвольный вектор y, который представим в виде суммы двух ортогональных компонент: y = z + v . Компонента z направлена вдоль вектора w и является проекцией y на w: z = dw, d = (y,w), а компонента v ортогональна этому вектору: (v,w) = 0, и равна v = y −(y,w)w. Тогда

Uy =U(z + v) = E(z + v) − 2ww^T(z + v) = z + v − 2ww^T z − 2ww^Tv =

= z + v − 2ww^Tdw = z + v − 2z = −z + v .

Таким образом, вектор Uy является зеркальным отражением вектора y относительно плоскости, ортогональной вектору w. Используя это свойство матрицы отражения, можно подобрать вектор w таким, чтобы исходный вектор y ≠ 0 в результате отражения Uy получил направление некоторого заданного единичного вектора e. В результате отражения получается вектор

Uy =αe или Uy = −αe , α = (y,y), (19)

поскольку при ортогональных преобразованиях длины векторов сохраняются (U – ортогональная матрица). Направление, перпендикулярное к плоскости отражения, будет определяться вектором (y −αe) или вектором (y +αe).

Таким образом, векторы

или , (20)

где , , являются требуемыми компонентами матрицы отражения. Если векторы y и e параллельны, то отражения делать не надо (при этом или будут равны нулю).

Покажем, что произвольную квадратную матрицу можно представить в виде произведения ортогональной и правой (верхней) треугольной матриц.

Пусть A – квадратная матрица порядка n.

Приведем ее к правой треугольной форме путем последовательного умножения слева на ортогональные матрицы отражения. На первом шаге приведения в качестве вектора y рассмотрим первый столбец матрицы A:

.

Если (i= 2,3,…,n), следует перейти к следующему шагу приведения, положив A⁽¹⁾ = A; U = E₁ и обозначив . В противном случае умножим матрицу A слева на матрицу отражения U₁=E_n−2w₁w₁^T, где w₁ подбирается таким образом, чтобы вектор U₁y₁ стал параллелен вектору e₁= [1, 0, 0, , 0]^T, то есть в соответствии с формулами (19), (20). Здесь E_n – единичная матрица порядка n, а e₁, y₁ – n–мерные векторы. В результате такого преобразования в первом столбце матрицы A⁽¹⁾ все элементы, кроме первого, станут равными нулю.

На втором шаге приведения преобразуемым вектором является второй

столбец матрицы A⁽¹⁾ без первого члена

.

Преобразование отражения выполняется умножением матрицу A⁽¹⁾ слева на матрицу

,

где S_n-1=E_n-1-2w_n-1w_n-1^T – (n −1) -мерный вектор, вычисляющийся по формулам (19), (20). Тем самым обнуляются элементы второго столбца, расположенные ниже главной диагонали матрицы A⁽²⁾ =U₂ A⁽¹⁾.

Последующие шаги процесса приведения матрицы A проводятся аналогично. После выполнения k-го шага получается матрица A^(k), все элементы которой, находящиеся ниже главной диагонали вплоть до k-го столбца матрицы, равны нулю: при i>j, j=1,2,…,k.

Для выполнения (k +1) -го шага приведения преобразуем вектор

.

Если компоненты вектора для (для i =(k+2), (k +3),…,n), получаем A^(k+1) = A^{(k )}; U_k+1 = E_n и переходим к следующему шагу. В противном случае строим матрицу отражения

S_k+1=E_n-k-2w_k+1w_k+1^T

(вектор w_k+1 и матрица S_k+1 порядка ( n − k )) для преобразования вектора y_k+1 в вектор, параллельный вектору e_k+1= [1, 0, 0, , 0]^T (длины ( n − k )), и переходим от матрицы A^{(k )} к матрице A^(k+1):

A^(k+1) = U_k+1A^{(k )}, где

Процесс этот всегда осуществим, и после (n −1) -го шага приходим к матрице

,

имеющей правую треугольную форму. Обозначив через U произведение матриц вращения , это выражение можно записать в виде A⁽ⁿ⁻¹⁾=UA, или A = QR, где Q =U^T – ортогональная матрица, а R = A⁽ⁿ⁻¹⁾ – правая треугольная матрица.

Решение системы Ax = b посредством метода отражения выполняется следующим образом. Умножив систему слева на последовательность матриц

отражения, сводим ее к виду с верхней треугольной матрицей

UAx =Ub  Rx =Ub, или A⁽ⁿ⁻¹⁾x =Ub.

Если все диагональные элементы матрицы A⁽ⁿ⁻¹⁾ отличны от нуля, то неизвестные x_i для i = n, (n −1),…,1 находятся, как и в методе Гаусса, обычным обратным ходом. Если же хотя бы один из диагональных элементов

матрицы равен нулю, то система A⁽ⁿ⁻¹⁾x =Ub вырождена, и в силу эквивалентности вырождена и исходная система.

Этот метод в настоящее время считается одним из наиболее устойчи-

вых к вычислительной погрешности, но более трудоемок в сравнении с методом Гаусса. Для получения QR-разложения квадратной матрицы A порядка n общего вида требуется около (4 / 3)n³ арифметических операций.