Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ФГБОУ ВО «Саратовский государственный технический университет имени Гагарина Ю.А.»
Задания и методические указания к выполнению курсовой работы по дисциплине «численные методы»
для студентов направления 27.03.04 «Управление в технических системах» (УПТС)
Саратов 2015
Цель работы
Ознакомление студентов с методами решения систем линейных алгебраических уравнений, получение навыков решения задач вычислительной математики на ЭВМ.
Задачи работы
Закрепление, углубление и расширение знаний студентов при решении практических вычислительных задач. Овладение вычислительными методами и практическими методами оценки погрешности вычислений. Приобретение умений и навыков при программировании и отладке вычислительных задач на компьютере.
Теоретическая часть
1. Прямые методы решения систем линейных алгебраических уравнений
1.1 Метод Гаусса
Одним из основных прямых методов решения СЛАУ является метод последовательного исключения неизвестных Гаусса. Он основан на возможности приведения исходной системы к эквивалентному представлению, когда относительно х решается задача с верхнетреугольной матрицей с единичной диагональю:
(1)
где
,
при j
< i.
Получение этой системы, т.е. построение матрицы U и вектора у составляют, так называемый, прямой ход метода исключения Гаусса. Дальнейшее решение системы Ux = у — обратный ход метода исключения.
а)
Прямой
ход исключения. Опишем
последовательно как он выполняется.
шаг.
Пусть
.
Тогда, деля первое уравнение на
,
получим
,
.
Комбинируя
полученное уравнение с остальными
уравнениями системы (1), исключая в них
переменную
,
найдем:
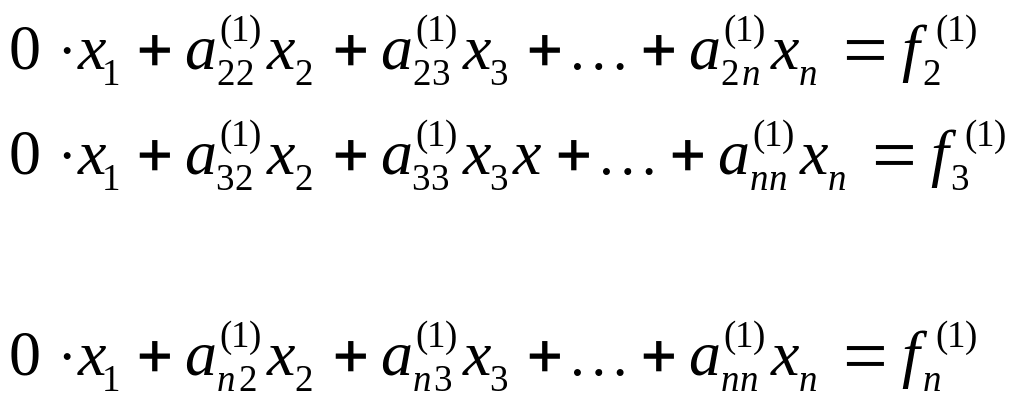
Для
оставшихся уравнений (без
),
повторим
описанную процедуру:
шаг.
После (s
— 1) шагов исключения часть переменных
исключена
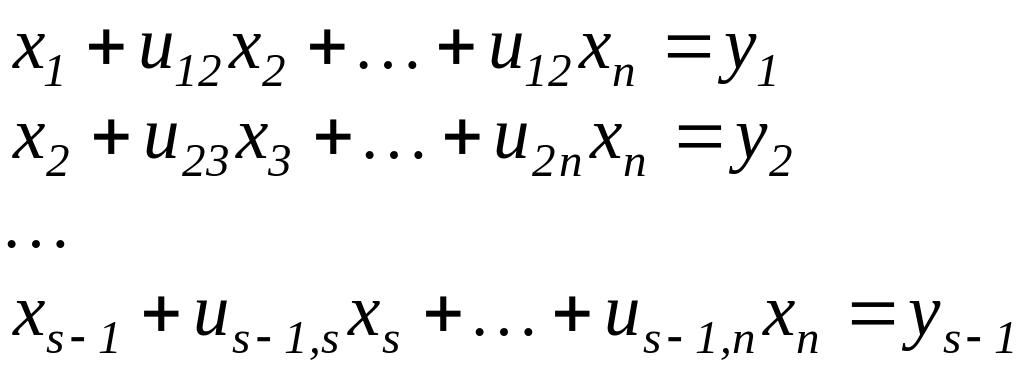
и мы получаем систему:
(
)
Положим
.
Делим s-oe
уравнение на
и
находим
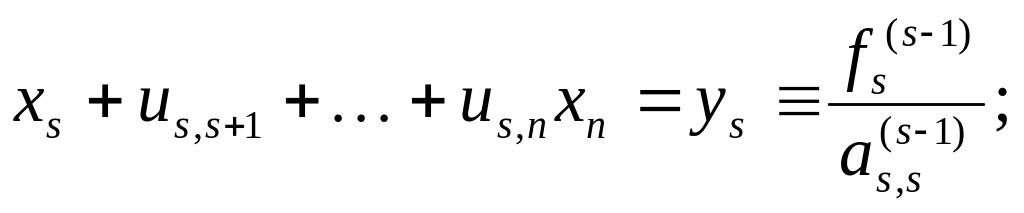
Используем
полученное уравнение. После умножения
его на
,
и
вычитания из i-гo
уравнения исключаем xs
в
системе (*) из остальных уравнений.
Получим
=
=
=
,
где
=
;
=
;
Таким образом прямой ход в методе Гаусса
осуществляется по формулам:
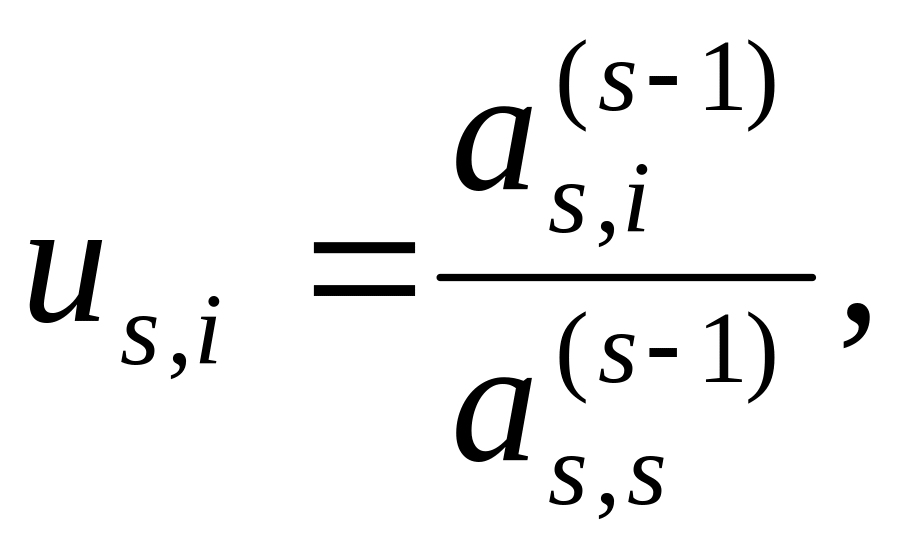s
= 1,. . . , n
; j
= s
+ 1,. . . , n
(4)
,
j
= s
+ 1, . . , n;
s
= 1,. . . , n
–
1
для матрицы и для правой части по формулам:
(5)
б)
Обратный
ход метода
Гаусса. Теперь решаем систему Ux
= у с
верхнетреугольной матрицей, причём
=
1:
(6)
Для реализации метода Гаусса требуется примерно (2/3)m3 арифметических операций, причем большинство из них приходится на прямой ход.
Ограничение
метода единственного деления заключается
в том, что
угловые элементы не равны нулю, т.е.
.