4. Формати використання функцій ode23 та ode45

ODE23 та ODE45 – функції для числового інтегрування систем звичайних диференціальних рівнянь першого порядку методом Рунге-Кутта. У функції ODE23 застосовується метод Рунге-Кутта 2-го або 3-го порядку, а в функції ODE45 – 4-го або 5-го порядку. Вибір порядку і кроку дискретизації здійснюється, в залежності від заданої точності обчислень, автоматично.

Формати використання обох функцій ідентичні. Розглянемо їх на прикладі функції ODE23.

[T, Y] = ode23('yprime', [T0, Tfinal], Y0) – повертає вектор-стовпець Т(m×1) та матрицю Y(m×n), які є розв’язком системи диференціальних рівнянь, заданої m-файлом на диску під іменем yprimе. Результати y_i(t_k) виводяться в матриці Y по стовпцях, тобто число стовпців матриці дорівнює порядку системи n, i=1,2,...,n, а число рядків m, k=1,2,...,m, – числу автоматично підібраних алгоритмом функції значень незалежної змінної t_k, виведених у вектор-стовпці T. Значення t_k є в межах [T0 Tfinal], де T0 та Tfinal початковий та кінцевий моменти часу, що обмежують діапазон часу, на якому потрібно одержати розв’язок системи рівнянь. Останнім вхідним параметром в цьому форматі використання функції ODE23 є вектор-стовпець початкових умов Y0.

'yprime' – символьна змінна – ім’я m-файлу на диску, яким задано систему диференціальних рівнянь. Цей файл створюють в довільному доступному системі редакторі за правилами мови програмування MATLAB та формату використання зовнішньої функції function і записують на диск в доступний системі каталог користувача. Вміст цього файлу – це вираз для обчислення матричної нелінійної функції (системи рівнянь), яка є правою частиною системи нелінійних диференціальних рівнянь, записаних у вигляді

.

Приклад 4.1.

Розв’язати систему нелінійних диференціальних рівнянь

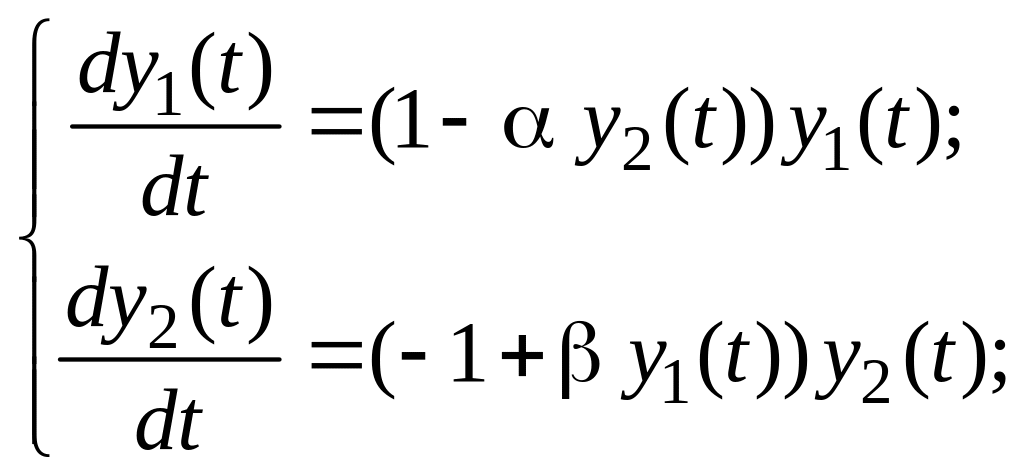(4.1)

в діапазоні зміни часу t[0; 15] для початкових умов .

Створимо на диску m-файл з іменем pryklad4_1:

function yp=pryklad4_1(t,y)

% файл до прикладу 4.1. Розв’язок системи нелінійних диференціальних

% рівнянь числовим методом з допомогою зовнішньої функції ODE23

% (ODE45) середовища програмування MATLAB.

% yp - вектор-стовпець ([dy₁/dt dy₂/dt]^T)

yp = diag([1 - 0.01*y(2), -1 + 0.02*y(1)])*y;

Записавши його на диск, введемо та виконаємо з командного рядка (в режимі прямих обчислень) наступні оператори:

» t0=0; tf=15; y0=[20 20]' % зауважимо, що y0 є вектором-стовпцем

» [t,y]=ode45('pryklad4_1',[t0,tf],y0)

У результаті обчислень одержимо вектор t та матрицю y.

Командою

»plot(t,y)

виведемо на екран дисплею графіки y₁(t) та y₂(t)

По замовчуванню обчислення здійснюються з точністю 1e-3. При необхідності її можна змінити, задаючи вхідний параметр точності у наступному форматі використання функції: [T, Y] = ode23(F, [T0, Tfinal], Y0, TOL).

У цьому разі обчислення будуть виконані з точністю, заданою величиною TOL.

Додаток 1 варіанти завдань

Побудувати та дослідити математичну модель відкритої протічної гідравлічної ємності. Значення конструктивних параметрів ємності та трубопроводів, вхідних та вихідних величин наведені в табл.1, значення вхідних величин – в табл.2. Графічне зображення об’єктів моделювання показано на рис.1-12.

Для графічного зображення об’єктів використані такі умовні графічні позначення:

Таблиця 1 Варіанти завдань до лабораторної роботи № 2 Для всіх варіантів прийняти: =1000 кг/м3, =10-5 Па∙с, =0,9.
Варіант	1	2	3	4	5	6	7	8	9	10	11	12
Рис.	1	2	3	4	5	6	7	8	9	10	11	12
Р1, кПа	8	15	40	-	10	5	3	2,5	25	-	4	30
Р2, кПа	0,5	-	0,2	0,4	0,1	0	0,1	1	0	0,3	0	0,6
L1, м	2	3	5	-	4	5	9	2	-	-	10	-
r1, м	0,05	0,1	0,07	-	0,09	0,09	0,1	0,08	-	-	0,08	-
L2, м	4	-	7	3	8	2	6	4	7	-	-	-
r2, м	0,06	-	0,08	0,07	0,05	0,09	0,08	0,1	0,1	-	-	-
kB, м2	-	-	-	-	-	-	-	-	0,006	0,008	0,004	0,005
l1	-	-	-	-	-	-	-	-	0,2	-	-	0,1
l2	-	-	-	-	-	-	-	-	-	0,3	0,95	0,9
q, л/с	-	10	-	15	-	-	-	-	-	30	-	-

Таблиця 2