Вопрос 38. Пропорционально-дифференцируемый (пд - регулятор)

Представляет собой параллельное соединение пропорционально и дифференциальной составляющей.

Динамические характеристики: ; АФХ ; АЧХ ; ФЧХ

С точки зрения качества переходных процессов ПД – регулятора обладает особенностями обеих простейших составляющих: наличие воздействие регулятора, благодаря чему уменьшается динамическая ошибка, установившихся режимов когда регулятор ведет себя как П – регулятор.

Вопрос 39. Пропорционально – интегральный регулятор (пи)

Динамические характеристики: ; АФХ: ; АЧХ

Система с ПИ – регулятором не дает статической ошибки. ПИ регулятор сочетает в себе достоинство обеих простейших составляющих. П составляющая обеспечивает достаточное быстродействие, а И составляющая ликвидирует статическую ошибку.

Механизм работы ПИ регулятора заключается в следующем: На начальном участке процесса регулирования основную роль играет пропорциональная составляющая так кА величина интегральной составляющей зависит не только от времени, и если , то интегральная составляющая тоже примерно ровна 0. С увеличением времени роль интегральной составляющей возрастает, что обеспечивает ликвидацию статической ошибки с тем большей скоростью чем больше

Вопрос 40. Пропорционально – интегрально дифференцируемый регулятор (пид)

АФХ

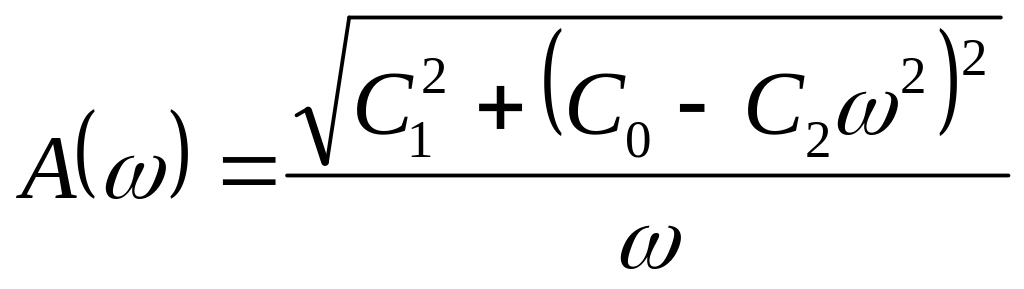АЧХ: ФЧХ

ПИД регулятор сочетает в себе достоинства всех 3^х составляющих. Высокое быстродействие (П – составляющей), малая динамическая ошибка (за счет воздействия по скорости) и отсутствие статической ошибки благодаря интегральной составляющей.

На рисунке представлено процессы регулирования одного и того же объекта, с различными регуляторами.

Необходимо отметить что применение регулятора с дифференциальной составляющей, не смотря на все преимущества не всегда целесообразно а иногда недопустимо.

Например для объекта с большим чистым запаздыванием бесполезно вводить воздействие по производной, так как она будет сказываться на выходе объекта, только по окончанию времени в объекте могут накопится большие отклонения.

П од оптимальными настройками понимают такие настройки которые для данного объекта обеспечивает процесс регулирования, удовлетворяющий выбранный критерий качества и ограничений.

Теория управления разработаны различные методы определения настроек, одни из которых более точны, но трудоемкие другие просты но приближенные.

Вопрос 41. Определение настроек регулятора методом расширенных частотных характеристик.

П ри изучении условий устойчивости замкнутой системы по критерию Найквиста было отмечено что если разомкнутая система разомкнута и ее АФХ проходит через точку то замкнутая система будет находится на границе устойчивости.

Введение степени колебательности, равносильно введению новой границе устойчивости вместо мнимой оси АОВ:

Тогда по аналогии с критерием Найквиста можно сформулировать условие при котором замкнутая система будет обладать с замкнутой заданной системой.

Если разомкнутая система обладает степенью колебательности не ниже заданной ее РАФХ проходит через точку , то замкнутая система будет обладать ее заданной степенью колебательности.

(*)

Полученное уравнение отражает связь между частотными характеристиками объекта и регулятора, вытекающего из условия обеспечения с заданной степенью колебательности.

Частотная характеристика объекта и выбранная степень калебательности m является заданным условием не известными остается настроечные параметры регулятора, и рабочая частота.

Н а 1^ом этапе определяется настройки регулятора сводятся к решению данной системы. Очевидно что для регулятора 2^мя и 3^мя настройками эта система имеет бесконечное множество решений. Поэтому только одной степени колебательности недостаточно, для нахождения настроек необходимо введение еще одного критерия, в качестве которого обычно используют интегральный квадратичный критерий, для которого оптимальное значение обеспечивает минимальное значение.

Расширенные настройки П - регулятора совпадают с обычными.

П : подставив в (*)

ПИ :

П одставим полученные уравнения в систему (*), получим выражение для настроек и

В этих уравнениях неизвестной величиной остается частота поэтому настройки соответственно степени колебательности может быть . Каждому значению частоты будет соответствовать своя пара настроек.

Если в плоскости настроечными параметрами построить кривые соответствуя различным степеням колебательности.

То эти кривые будут разбивать на 2 зоны, нижняя будет соответствовать большим значениям степени колебательности, а верхнее меньшим значением.

Кривая , разбивает на зону устойчивости и неустойчивости.

Сравнив между собой процессы регулирования соответствующим различным точкам на кривой раной колебательности М. В точке 1 отсутствует интегральная составляющая и в процессе регулирования появляется статическая ошибка. В точке 2 интегральная составляющая не значительна, статическая ошибка равна 0, но скорость устранения мала и переходный процесс характеризует затянувшимся хвостом. Увеличение интегральной составляющей сопровождается уменьшением рабочей частоты и ростом динамической ошибки точка 4. Расчет интегрального квадратичного критерия показал что его минимальное значение соответствует точке, не много сдвинутой в право относительно Max. Точка 3 рабочая частота в этой точке определяется

Таким образом методика нахождения настроек ПИ - регулятора сводится к следующему:

1) Расчет расширенных характеристик объекта.

2) Расчет и построение кривой равной колебательности, плоскости настроек и по формулам (1) и (2).

3) Нахождение по полученному графику рабочей частоты и соответствие ее оптимальных настроек.

ПИД – регулятор

Т ак же как Пи регулятор имеет две настройки и , методика расчета аналогична.

( *)

С помощью полученных формул из системы (*) выражаем настройки и :

Подставим полученные формулы различных частот строим кривую равной колебательности:

На графике представлены различные переходные процессы с различными значениями настроек. В точке 1 кривой равной колебательности дифференциальной составляющей , регулятор ведет себя как довольно большой динамической и статической ошибкой. При движении в право по кривой наблюдается уменьшение статической и динамической ошибки. Дальнейшее увеличение настроек , приводит к уменьшению динамической ошибки но растет статическая. Поэтому оптимальными настройками являются соответствующие точке 2 чуть-чуть смещенные относительно max.

У ПИД регулятора 3 параметра настроек и поэтому, его расчет по методу расширенных частотных характеристик несколько сложнее чем для регулятора с 2^мя параметрами.

Полученные формулы подставляем в рассмотрение ранее систему откуда выражаем и : Для ПИД регулятора вместо плоскости параметров мы получим 3^х мерное пространство. В этом случае расчет настроек производится следующим образом, задаваясь различными значениями строят кривые равные колебательности в плоскости и :

Э ти графики должны быть аналогичны тем что получили для ПИ – регулятора, поскольку ПИ регулятор это частный случай ПИД регулятора у которого третья настройка ровна нулю. Затем для каждого графика находим оптимальные настройки и , сравнивая между собой переходные процессы соответственно теми или иными настройками. Выбирают оптимальный для которого интегральный квадратичный критерий будет оптимальным.