Вопрос 28. Общее условие устойчивости линейной системы.

Общим условием устойчивости линейной системы является расположение всех корней характеристического уравнения в левой полуплоскости.

Наличие корней на мнимой оси говорит о том что система находится на границе устойчивости.

Однако на практике пользоваться этим условием для проверки устойчивости довольно трудно. Это связанно с тем что реальные объекты описываются дифференциальным уравнением высоким порядком или содержит звенья чистого запаздывания. Для таких систем разработаны критерия устойчивости, которые позволяют оценить устойчивость системы по другим признакам:

1) Алгебраический критерий Раусса–Гурвица

2) критерий Михайлова

3) АФ критерий Найквиста

Вопрос 29. Критерий устойчивости Раусса–Гурвица.

Пусть система описывается дифференциальным уравнением N^го порядка (нумерация коэффициентов здесь проводится в обратном порядке по сравнению со стандартным дифференциальным уравнением)

Составим из коэффициентов этого уравнения сатрицу следующего вида

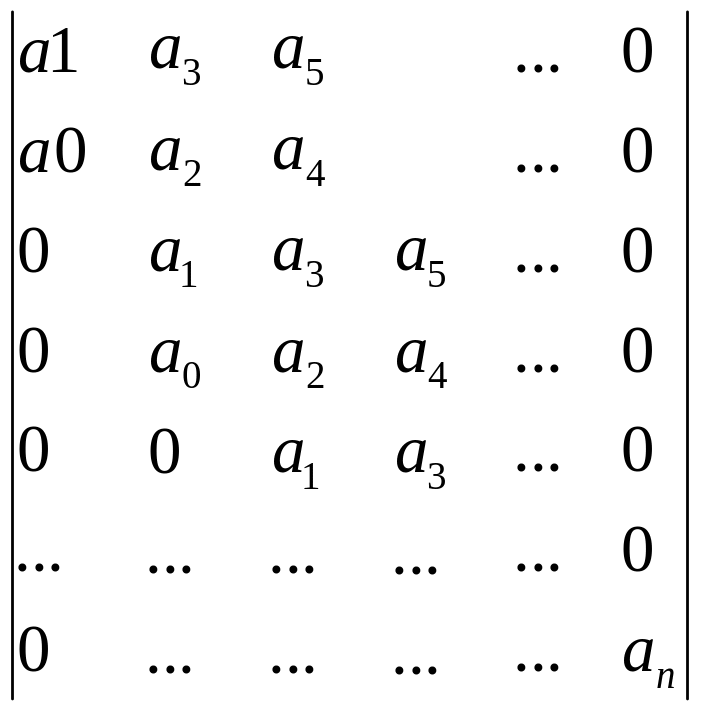
Коэффициенты расставляются следующим образом, в главную диагональ, записывается все коэффициенты начиная с по затем заполняется столбцы таким образом чтобы над диагональю подряд располагаются коэффициенты с возрастающей, а под диагональю с убывающей.

Свободные элементы матрицы заполняются нулями. В результате все нечетные строки содержат коэффициенты с нечетными номерами, а четные только с нечетными. Причем каждая следующая пара строк смещается на один столбец. Для этого определителем запишем диагональный миноры которые определяются Раусса–Гурвица

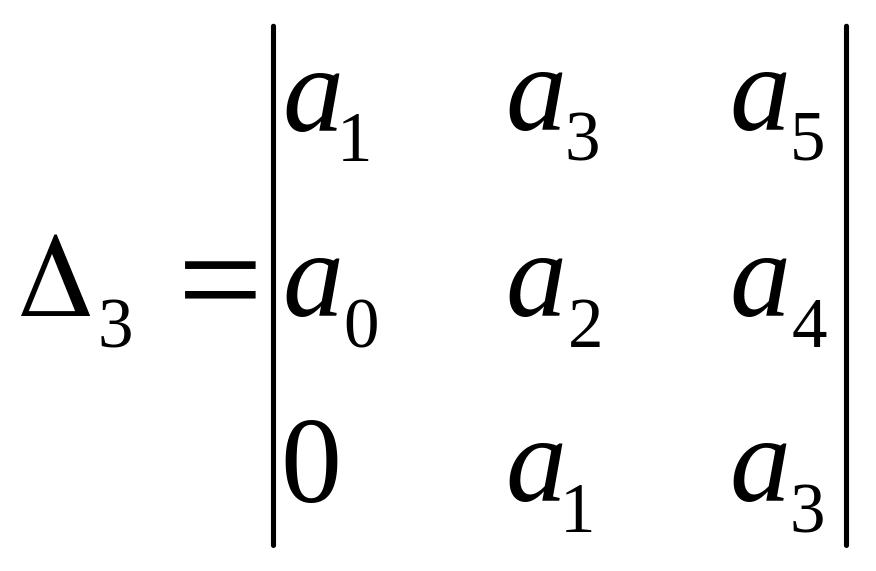
В соответствии с критерием Раусса–Гурвица для того чтобы линейная система была устойчивой, необходимо и достаточно чтобы все определители были положительными.

Если хотя бы один определитель отрицательный, система будет не устойчива. Если хотябы один определитель равен нулю, система будет на границе устойчивости.

Применим критерий Гурвица к уравнениям 1^го 2^го 3^го порядка

1^го)

2^го)

3^го)

Таким образом для системы 1^го и 2^го порядка условием устойчивости является положительность всех коэффициентов. Для систем более высокого порядка это условие недостаточно и на коэффициенты накладывается дополнительное ограничение. В частности для систем 3^го порядка необходимо произведение средних коэффициентов было больше произведение крайних.

Пример

Вопрос 30. Критерий Михайлова

К ак и в случае алгоритм критерия, критерий Михайлова применяется тогда когда известно дифференциальное уравнение . Для анализа устойчивости системы предлагается использовать характеристический комплекс б который определяется из характеристического уравнения: заменой оператора Лапласа на величину определим действительную и миную части . В действительной части будут слагаемые характеристического уравнения содержащий в четной степени: . В мнимой части отсутствуют слагаемые в которых оператор Лапласа имеет четную степень:

Если в уравнении для характеристического комплексного подставить мы получим комплексное число , на комплексной плоскости это будет вектор соединяющий начало координат и точку с координатой

При изменений частоты от 0 до этот вектор нарисует в комплексной плоскости кривую, который называется годограф Михайлова.

Формулировка критерия Михайлова.

Замкнутая система устойчива если годограф Михайлова начинается на действительной положительной полуоси огибает с ростом частоты от 0 до против часовой стрелки в начало координат, проводя при этом, последовательно N квадрантов. Где N – степень характеристического уравнения.

На рисунке кривая 1 соответствует устойчивому состоянию.

Кривые с 3 по 7 неустойчивых систем.

У словия нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат. В этом случае существует значение при котором . А значит имеется два чисто мнимых корня. Это означает что в системе имеется не затухающиеся колебания и не значительное изменение параметров в системе, приведут к тому что годограф Михайлова сместится в право или вниз и система может стать либо устойчивой либо неустойчивой.

Следствие критерия Михайлова.

Система устойчива, если годограф Михайлова последовательно пересекает вещественную и мнимую оси, начиная с на вещественной оси, следовательно необходимо и достаточно что точки пересечения годографа Михайлова в положительной и отрицательной полуоси передавались, то есть.

При практическом построении прежде всего находят точку пересечения годографа с координатными осями. Для этого решают уравнения и находят частоты при которых годограф пересекает мнимую ось подставив значения частот в уравнение вычисляют соответственно ординаты. Аналогично определяются точки пересечения с действительной осью.

Пример.

Для данного:

Н айдем точку пересечения с мнимой осью V. Это уравнение действительной корней не имеет стало быть годограф Михайлова не пересекает мнимую часть.

Дальнейший расчет можно не проводить так как из первого заключения ясно что система не устойчива. Годограф устойчивой системы 5^го порядка должен проходить так, показано пунктиром.

Пример 2