6.2. Дисперсия и среднеквадратическое отклонение.

При решении практических задач могут встретиться случайные величины, имеющие разные распределения, но одинаковые математические ожидания. При этом у одних из этих величин отклонения значений от математического ожидания небольшие, у других, наоборот, могут быть значительными. Иначе говоря, у величин может быть разный разброс значений вокруг математического ожидания.

Например, для двух дискретных случайных величин, заданных следующими законами:

Х	-1	0	1	и	Y	-100	0	100
Р	0,3	0,4	0,3		Р	0,2	0,6	0,2

математические ожидания равны, т.е. М(Х)=М(Y)=0. Однако, понятно, что это разные случайные величины и, прежде всего, они отличаются разбросом значений по оси абсцисс слева и справа от точки 0 – своего математического ожидания.

Приведенные рассуждения говорят о том, что было бы целесообразно ввести в рассмотрение некоторую числовую характеристику, связанную с разбросом. На первый взгляд может показаться, что такой характеристикой может быть среднее значение всех отклонений возможных значений случайной величины от математического ожидания.

Отклонением случайной величины Х от своего математического ожидания М(Х) называется разность между случайной величиной и ее математическим ожиданием.

Очевидно, что отклонение также является случайной величиной. Найдем среднее значение отклонения, т.е. математическое ожидание отклонения, получим M(X – M(X)) = M(X) – M(M(X)) = M(X ) – M(X) = 0.

Итак, математическое ожидание отклонения случайной величины равно нулю. Этот факт можно объяснить также тем, что возможные значения отклонения имеют как положительные, так и отрицательные знаки, поэтому при нахождении среднего значения (математического ожидания) слагаемые взаимно уничтожаются. Избежать этого можно, убрав отрицательные знаки значений отклонения. Для этого эти значения либо берут по абсолютной величине, либо возводят в квадрат. Первый путь используется крайне редко, так как работа с абсолютными величинами вызывает, как правило, серьезные трудности, например, при дифференцировании. Поэтому в качестве характеристики разброса используют математическое ожидание квадрата отклонения.

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата отклонения данной случайной величины от своего математического ожидания, т.е.

D(X) = M[(X – M(X))²] (6.4)

Само слово "дисперсия" означает "рассеивание".

Нетрудно понять, что вероятности значений случайных величин Х и (X – M(X))² одинаковы. Для того, чтобы величина (X – M(X))² приняла значение, например, (х₁ – M(X))², достаточно, чтобы случайная величина Х приняла значение х₁. Вероятность этого события равна р₁, следовательно, и вероятность того, что величина (X – M(X))² примет значение (х₁ – M(X))² также равна р₁. Аналогично обстоит дело и с остальными возможными значениями. Поэтому формула (6.4) с учетом определения математического ожидания случайной величины примет вид:

для дискретной случайной величины с конечным множеством значений

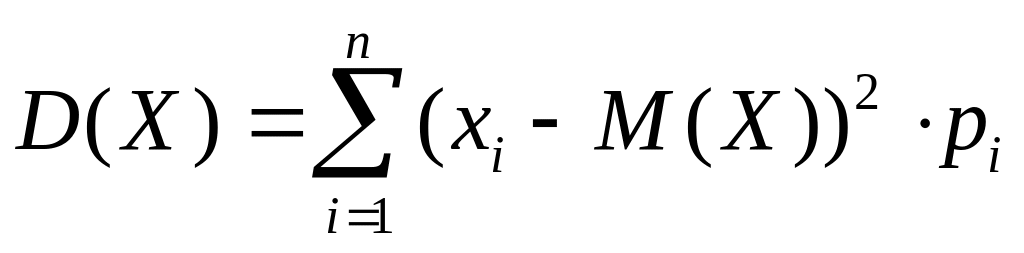; (6.5)

для непрерывной случайной величины

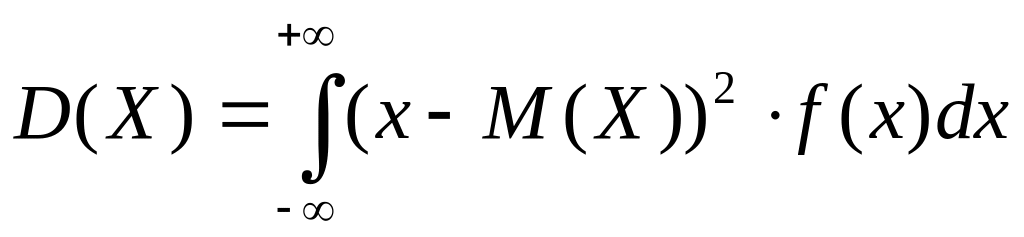(6.6)

Несобственный интеграл в формуле (6.6) превращается в определенный интеграл по конечному промежутку , если значения непрерывной случайной величины имеются только в этом промежутке.

Математическое ожидание имеет ту же размерность, что и сама случайная величина, в отличие от дисперсии, которая имеет размерность, равную квадрату размерности случайной величины. Таким образом, дисперсия характеризует не сам разброс, а квадрат разброса значений случайной величины. Для того чтобы определить сам средний разброс находят квадратный корень из дисперсии и получают новую числовую характеристику, называемую среднеквадратическим отклонением.

Среднеквадратическим отклонением σ(Х) случайной величины Х называется квадратный корень из дисперсии, т.е.

.

Пример 6.6. Найти дисперсию дискретной случайной величины, заданной следующим рядом распределения

Х	1	2	5
Р	0,3	0,5	0,2

Решение. Найдем вначале математическое ожидание данной случайной величины, получим М(Х)=1·0,3+2·0,5+5·0,2=2,3.

Найдем закон распределения величины (Х - М(Х))²:

(Х - М(Х))2	(1 - 2,3)2	(2 – 2,3)2	(5 – 2,3)2
Р	0,3	0,5	0,2

После вычислений, получим

(Х - М(Х))2	1,69	0,09	7,29
Р	0,3	0,5	0,2

Найдем математическое ожидание полученной случайной величины: D(X) = M[(X – M(X))²]=1,69·0,3+0,09·0,5+7,29·0,2=2,01. ■

Пример 6.7. Найти дисперсию непрерывной случайной величины, заданной своей функцией плотности: f(x)=0,5x при х(0,2); для остальных х функция плотности равна нулю.

Решение. По формуле (6.2) найдем математическое ожидание, получим

.

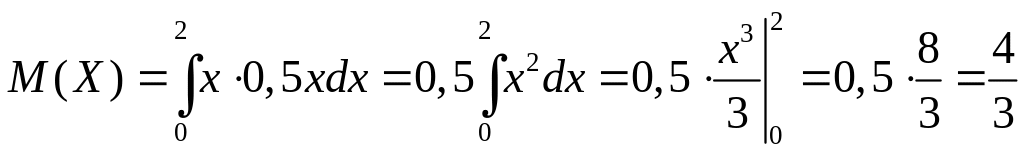По формуле (6.6) найдем дисперсию, при этом несобственный интеграл превратится в определенный по заданному промежутку (0,2):

. ■

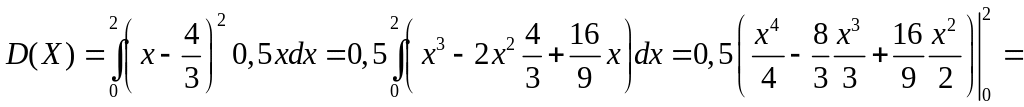
Для вычисления дисперсии часто применяется другая формула, которая легко получается из формулы (6.4).

Теорема 6.1. Дисперсия случайной величины равна разности между математическим ожиданием квадрата этой случайной величины и квадратом математического ожидания:

D(X) = M(X²) – M²(X) (6.7)

Доказательство. Преобразуем формулу (6.4), используя свойства математического ожидания, получим

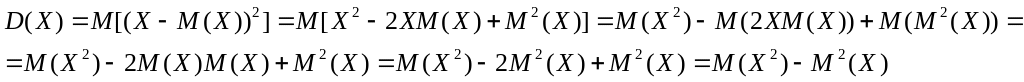Теорема доказана.

Пример 6.8. Решим пример 6.6, используя формулу (6.7). Математическое ожидание было найдено, оно равно М(Х)=2,3. Теперь найдем закон распределения величины Х², получим

Х2	1	4	25
Р	0,3	0,5	0,2

Найдем М(Х²) = 1·0,3 + 4·0,5 + 25·0,2 = 7,3. Тогда дисперсия равна

D(Х) = 7,3 – (2,3)² = 2,01. ■

Очевидно, что применение формулы (6.7) значительно упрощает процесс нахождения дисперсии. Понятно, что эту же формулу можно применять и для нахождения дисперсии непрерывной случайной величины.