Министерство образования и науки Российской Федерации

Рязанский институт (филиал)

федерального государственного бюджетного образовательного

учреждения высшего образования

«Московский государственный машиностроительный университет (МАМИ)»

Кафедра высшей математики и информатики с.В. Челебаев, н.В. Гречушкина логические основы информатики

Методические указания к практическим работам

для студентов бакалавриата и специалитета, обучающихся по направлениям подготовки 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств» и

08.05.01 «Строительство уникальных зданий и сооружений»

Рязань

2016

УДК 681.3

ББК 74.202

Ч38

Челебаев С.В., Гречушкина Н.В.

Ч38 Логические основы информатики: Методические указания к практическим работам / С.В. Челебаев, Н.В. Гречушкина. Рязань: Рязанский институт (филиал) Университета машиностроения. 2016. – 28 с.

Методические указания предназначены для студентов первого курса, обучающихся по направлениям подготовки 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств» и 08.05.01 «Строительство уникальных зданий и сооружений».

В методических указаниях изложены логические операции, логические элементы, правила построения комбинационно-логических схем, базисы логических операций, правила перевода логических выражений между базисами.

Приведены варианты для самостоятельных и проверочных работ.

Печатается по решению методического совета Рязанского института (филиала) Университета машиностроения.

УДК 681.3

ББК 74.202

Ó Челебаев С.В., 2016 Ó Гречушкина Н.В., 2016 Ó Рязанский институт (филиал)     Университета машиностроения,

Содержание

1 Высказывания и логические операции…………………………………………..4

2 Алгебра логики…………………………………………………………………….9

3 Переход между базисами…………..…………………………………………….18

Введение

Алгебра логики (алгебра высказываний) и основы математической логики играют важную роль в информатике. Математическая логика присутствует в различных разделах информатики в виде:

1) двоичной логики, на которой основана работа цифровых компьютеров;

2) специальной алгебры логики, лежащей в основе математической модели реляционных баз данных;

3) правил, определяющих функционирование алгоритмов и программ, работу интеллектуальных и экспертных систем.

1 Высказывания и логические операции

Основным понятием математической логики является понятие простого высказывания.

Высказывание – это повествовательное предложение, утверждающее что-либо о чем-либо, о котором можно сказать, истинно оно или ложно в данных условиях. Логическими значениями высказываний являются «истина» и «ложь».

В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения. Каждое высказывание либо истинно, либо ложно, и ни одно высказывание не может быть одновременно истинным и ложным.

Пример. Рязань – столица РФ. Значение высказывания – «ложь».

Москва – столица РФ. Значение высказывания «истина».

Высказывание, представляющее собой одно утверждение, принято называть простым, или элементарным.

Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если», «то», «тогда и только тогда», принято называть сложными, или составными.

Пример. Карась не рыба. Значение высказывания – «ложь».

Элементарные высказывания обозначаются малыми буквами латинского алфавита; истинное значение высказывания цифрой 1, а ложное значение — цифрой 0. Например, если высказывание x истинно, то будет справедлива запись x = 1, если высказывание x ложно, то x = 0.

При изучении логики высказываний предполагается, что все простые высказывания, входящие в рассмотрение, обладают одним из двух свойств — являются истинными либо ложными. Поэтому и само высказывание может быть истинно или ложно.

Над высказываниями можно выполнять логические операции:

1) отрицание;

2) конъюнкция;

3) дизъюнкция;

4) импликация;

5) эквивалентность и др.

Операция отрицания высказывания х обозначается и читается «не х» или «неверно, что х».

Отрицание высказывания – это новое высказывание, которое является истинным, если высказывание x ложно, и ложным, если высказывание x истинно.

Таблица 1 – Таблица истинности логической операции НЕ (инверсия, отрицание)

Аргумент	Результат
x
0	1
1	0

Рисунок 1 – Инвертор

Пример. Ока впадает в Волгу. Значение – «истина».

Ока не впадает в Волгу. Значение – «ложь».

Операция конъюнкции высказываний и обозначается символом , а выражение читается « ». Высказывания и называются членами конъюнкции.

Конъюнкция (логическое умножение) высказываний – это новое высказывание, которое считается истинным, если все высказывания, входящие в конъюнкцию истинны, и ложным, если хотя бы одно из высказываний ложно.

Таблица 2 – Таблица истинности логической операции И

Аргумент		Результат
0	0	0
0	1	0
1	0	0
1	1	1

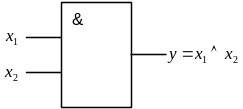
Рисунок 2 – Конъюнктор

Пример. Пусть x1: Ока впадает в Волгу. Значение – «истина».

x2: Рязань – столица РФ. Значение – «ложь».

Тогда примет значение «ложь».

Операция дизъюнкции высказываний и обозначается символом , а выражение читается как « ». Высказывания и называются членами дизъюнкции.

Дизъюнкция (логическое сложение) высказываний – это высказывание, которое считается истинным, если хотя бы одно из высказываний, входящих в дизъюнкцию истинно. Результатом дизъюнкции будет ложь, если ложны все высказывания, входящие в дизъюнкцию.

Таблица 3 – Таблица истинности логической операции ИЛИ

Аргумент		Результат
0	0	0
0	1	1
1	0	1
1	1	1

Рисунок 3 – Дизъюнктор

Пример. Пусть x1: Ока впадает в Волгу. Значение – «истина».

x2: Рязань – столица РФ. Значение – «ложь».

Тогда примет значение «истина».

Операции И, ИЛИ, НЕ образуют булевый (логический) базис. Базис – это такой набор логических функций, с помощью которого можно построить любую сколь угодно сложную логическую функцию.

Таблица 4 – Таблица истинности логической операции И-НЕ (отрицание конъюнкции, штрих Шеффера)

Аргумент		Результат
0	0	1
0	1	1
1	0	1
1	1	0

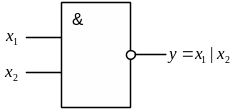
Рисунок 4 – Элемент И-НЕ (элемент Шеффера)

Операция И-НЕ образует базис Шеффера.

Таблица 5 – Таблица истинности логической операции ИЛИ-НЕ (отрицание дизъюнкции, стрелка Пирса)

Аргумент		Результат
0	0	1
0	1	0
1	0	0
1	1	0

Рисунок 5 – Элемент ИЛИ-НЕ (элемент Пирса)

Операция ИЛИ-НЕ образует базис Пирса.

Таблица 6 – Таблица истинности логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ (eXclusive OR, функция нечетности)

Аргумент		Результат
0	0	0
0	1	1
1	0	1
1	1	0

Рисунок 6 – Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ

Операция «исключающее ИЛИ» используется при построении суммирующих устройств ЭВМ.

Операция импликации высказываний и обозначается символом , а выражение читается как «если х, то у». Высказывание называют условием, или посылкой, высказывание — следствием, или заключением, а высказывание — следованием, или импликацией.

Импликация двух высказываний и – это новое высказывание, которое считается ложным, если – истинно, а – ложно, и истинным во всех остальных случаях.

Таблица 7 – Таблица истинности логической операции ИМПЛИКАЦИЯ

Аргумент		Результат
0	0	1
0	1	1
1	0	0
1	1	1

Пример. Пусть x1: Число 12 делится на 6. Значение – «истина».

x2: Число 12 делится на 3. Значение – «истина».

Тогда отражает высказывание «Если число 12 делится на 6, то оно делится на 3» и является истинным.

Операция эквивалентности высказываний и обозначается символом , а выражение читается «для того чтобы , необходимо и достаточно, чтобы » или « тогда и только тогда, когда ». Высказывания и называются членами эквивалентности.

Эквивалентность двух высказываний и – это новое высказывание, которое считается истинным, если оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.

Таблица 8 – Таблица истинности логической операции ЭКВИВАЛЕНТНОСТЬ

Аргумент		Результат
0	0	1
0	1	0
1	0	0
1	1	1

Пример. Высказывание : «Треугольник SPQ с вершиной S и основанием PQ – равнобедренный», высказывание : «В треугольнике SPQ с вершиной S и основанием PQ », можно записать высказывание «Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда » в форме эквивалентности . Эквивалентность является истинной, так как высказывания либо одновременно истинны, либо одновременно ложны.