Индивидуальное домашнее задание № 1

1. Вычислить произведения матриц а∙в и в∙а, если

А = , В= .

Решение. Воспользуемся определением произведения матриц С = A∙B: произведением матрицы А_m×n = (a_ij) на матрицу B_n×k = (b_ij) называется матрица C_m×k = (c_ij), элемент ij c которой равен сумме произведений элементов строки с номером i матрицы А на соответствующие элементы столбца с номером j матрицы В:

c_{ij =} a_i1 b_1j + a_i2 b_2j + a_in b_nj = a_im b_mj (1.1)

Как видно из формулы (1.1) произведение матриц возможно только в случае согласованности матриц: если число столбцов первой матрицы совпадает с числом строк второй. В противном случае произведение матриц невозможно. Проверим согласованности заданных матриц А и В. Размер матрицы А=(2х3), В=(3х2). Внутренние значения размеров матриц совпадают. В результате произведения получим матрицу размером (2х3)(3х2)=(2х2):

A∙B = ∙ =

= .

Проверим возможность произведения заданных матриц B и A. (3х2)(2х3)=(3х3). Внутренние значения размеров матриц совпадают. В результате произведения получим матрицу размером (3х3):

B∙A = ∙

= .

2. Вычислить определитель:

Решение. Воспользуемся теоремой о разложении определителя по строке:

=

А₁₁, А₁₂, А₂₂, А_1n, A_n2 - алгебраические дополнения к элементам а₁₁, а₁₂, а₂₂, а_1n, а_n2 . По определению алгебраического дополнения:

А_ij = М_ij ,

М_ij – минор элемента а_ij , то есть определитель, оставшийся после вычеркивания i – той строки и j – того столбца. Например, M₃₄ – минор элемента а₃₄ = 4.

М₃₄ = .

Разложение определителя можно проводить по элементам любого ряда.

= 1∙ А₁₁ + 2∙А₁₂ + 4∙А₁₃ + 7∙А₁₄ .

= 1∙ + 2∙ + 4∙ + 7∙ .

Продолжим вычисление определителей третьего порядка, разлагая их по первым строкам:

= -3∙ + 1∙ = -3∙1∙ (2∙5 - 4∙4) – (1∙5 - 4∙(-4)) + 6∙1∙ (1∙4 - 2∙(-4)) = 18 – 21 + 72 = 69

= 2∙ + 1∙ = 2 ∙1∙ (2∙5 - 4∙4) – (1∙5 - 4∙3) + 6 ∙(1∙4 - 2∙3) = -12 + 7 – 12 = -17

= 2∙ -3∙ + = 2 ∙1∙ (1∙5 - 4∙(-4)) + 3 ∙ (1∙5 - 4∙3) + 6 ∙ (1∙(-4) - 1∙3) = 42 – 21 – 42 = -21

= 2∙ - 3∙ + 1∙ = 2 ∙1∙ (1∙4 – (-4)∙2) + 3∙(1∙4 - 2∙3) + (1∙ (-4) -1∙3) = 24 - 6 – 7 =11

= 1∙ ∙69 + 2∙ ∙ (-17) + 4∙ ∙ (-21) + 7∙ ∙23 = 69 + 34 - 84 - 77 = -58

3. Решить матричное уравнение:

∙ Х - 3∙ = 5∙

Решение. Выразим в явном виде выражение, содержащее неизвестное:

∙ Х = 5∙ + 3∙

∙ Х = +

∙ Х = +

∙ Х =

∙ Х =

Обозначим матрицы:

А = , В = . Получим матричное уравнение:

А∙ Х = В (1)

Чтобы выразить неизвестную матрицу Х необходимо помнить, что операция деления на матрицу не определена, однако определена обратная матрица . Кроме того, необходимо помнить, что произведение матриц не коммутативно:

А∙В ≠ В∙А.

Поэтому, чтобы выразить неизвестную матрицу Х, нужно воспользоваться определением обратной матрицы А∙ = Е или А = Е (Е – единичная матрица) и домножить обе части уравнения (1) на слева. Получим:

∙ А∙ Х = ∙ В

Е∙ Х = ∙ В

Умножение любой матрицы на единичную не изменяет матрицы, поэтому решение уравнения будет находится как:

Х = ∙ В

Воспользуемся схемой построения обратной матрицы:

= .

Вычислим для А = .

det A = 6 – 1 = 5,

А₁₁ = ∙ 3 = 3, А_{12 =} ∙ 1 = -1

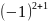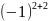А₂₁ = ∙ 1 = -1, А₂₂ = ∙ 2 = 2.

= .

Вычислим неизвестную матрицу Х:

Х = ∙ = = = .