20) Теорема Крамера.

Пусть (дельта)-определитель матрицы системы А, а (дельта)i-определитель матрицы, получается из матрицы А заменой j-го столбца столбцов свободных чисел. Тогда, если (дельта) не равна 0,то система имеет единственное решение, определяемое во формуле:

1.Определитель 2-го порядка вычисляется по формуле  

2. Определитель третьего порядка вычисляется по формуле

 

Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).

21) Определителем матрицы А (определителем n-го порядка) называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. При этом произведение берётся со знаком «+», если подстановка из индексов входящих в него элементов чётная, и со знаком «-» в противном случае.

Обозначение определителя: |А| = .

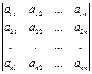Пусть задана квадратная матрица An×n (т.е. квадратная матрица n-го порядка).

Минором Mij элемента aij матрицы An×n именуют определитель матрицы, полученной из матрицы A вычёркиванием i-й строки и j-го столбца (т.е. строки и столбца, на пересечении которых находится элемент aij).

Алгебраическое дополнение Aij элемента aij

Пусть задана квадратная матрица An×n (т.е. квадратная матрица n-го порядка).

Алгебраическое дополнением Aij элемента aij матрицы An×n находится по следующей формуле: Aij=(−1)i+j⋅Mij, где Mij – минор элемента aij.

Часто вместо словосочетания "минор элемента матрицы" в литературе встречается "минор элемента определителя". Суть остается неизменной: чтобы получить минор элемента aij нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента aij.

22) Свойства определителей

Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен нулю.

Если все элементы какой-либо строки (столбца) матрицы умножить на число λ, то её определитель умножится на это число λ.

При транспонировании матрицы её определитель не изменится.

При перестановке 2-х строк (столбцов) матрицы её определитель меняет знак на противоположный.

Если матрица содержит две одинаковые строки (столбца), то её определитель равен нулю.

Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен нулю.

Если все элементы какой-либо строки (столбца) матрицы умножить на число λ, то её определитель умножится на это число λ.

При транспонировании матрицы её определитель не изменится.

При перестановке 2-х строк (столбцов) матрицы её определитель меняет знак на противоположный.

Если матрица содержит две одинаковые строки (столбца), то её определитель равен нулю.

Теорема (частный случай теоремы Лапласа)

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

Δ=ai1Ai1+ai2Ai2+…+ainAin.

Значение теоремы состоит в том, что позволяет свести вычисление определителей n-го порядка к вычислению более простых определителей (n-1)-го порядка.

23) Для вычисления определителя n-го порядка необходимо знать и использовать следующую теорему.

Теорема Лапласа. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т.е.

Определение. Если в определителе n-го порядка выбрать произвольно p строк и p столбцов (p < n), то элементы, находящиеся на пересечении этих строк и столбцов, образуют матрицу порядка .

Определитель этой матрицы называется минором исходного определителя. Например, рассмотрим определитель :

24) Матрица называется обратной к матрице , если , где - единичная матрица. Матрица , для которой существует обратная матрица, называется обратимой.

Так как равенство возможно лишь для квадратных матриц одинакового размера, то обратимой может быть лишь квадратная матрица. Однако, не каждая квадратная матрица обратима.

Матрица обратима тогда и только тогда, когда она не вырождена.

Квадратная матрица называется вырожденной, если , и невырожденной, если .

Теорема 2 (единственность существования обратной матрицы). Если у матрицы существует обратная матрица, то она является единственной.

Доказательство. Применим метод от противного. Предположим, что нашлась матрица А для которой существуют две различные обратные матрицы В и С:

, . Тогда, так как , то умножая обе части равенства слева на матрицу, получаем , , , .

И этого следует, что матрицы А и В – равные. Противоречие. Следовательно, если у матрицы существует обратная, то она единственная. Теорема доказана.