1) Координатой точки на координатной оси называется число , определяемое правилом:

если точка совпадает с точкой , то полагают ;

если точка отличается от точки , то

а) равно длине отрезка , когда направление от точки к точке совпадает с положительным направлением оси , и

б) равно длине отрезка, взятой со знаком минус, когда направление от точки к точке противоположно направлению оси .

Пишут: .

Таким образом, каждой точке на координатной оси соответствует одно единственное число, и обратно, каждому числу соответствует одна единственная точка на этой прямой, то есть установлено взаимно-однозначное соответствие между точками прямой и действительными числами. Поэтому, когда говорят «дана точка», следует понимать, что дана ее координата. Если говорят «найти точку», следует понимать, что нужно найти координату искомой точки.

2. Прямоугольная декартова система координат

Прямоугольную декартову систему координат вводят следующим образом:

а) выбирают две взаимно перпендикулярные оси координат — ось , или ось абсцисс, и ось , или ось ординат;

б) точку их пересечения — точку называют началом координат.

Определение 2. Координатами точки на плоскости называются числа и , определяемые правилом:

1) Из точки опускают перпендикуляры на оси и . Получают проекцию точки на оси — точку и проекцию точки на оси — точку .

2) Находят координату точки на оси , это число , и координату точки на оси , это число . Тогда числа и есть координаты точки , при чем — абсцисса, а — ордината точки . Пишут: .

Оси координат делят всю плоскость на четыре части (четыре координатных угла, четверти, четыре квадранта), при этом

Все точки оси имеют ординаты, равные нулю, точки оси — абсциссы, равные нулю.

Если дана пара чисел , то можно построить единственную точку, имеющую эти числа в указанном порядке своими координатами. Для этого на осях строят точки , имеющие числа своими координатами соответственно. Из точки восстанавливают перпендикуляр к оси , из точки восстанавливают перпендикуляр к оси . Точка пересечения этих перпендикуляров есть искомая точка . Таким образом, введено взаимно однозначное соответствие между точками плоскости и парами чисел

Формулы вычисления расстояния между двумя точками:

Формула вычисления расстояния между двумя точками A(x_a, y_a) и B(x_b, y_b) на плоскости:

AB = √(x_b - x_a)² + (y_b - y_a)²

Формула вычисления расстояния между двумя точками A(x_a, y_a, z_a) и B(x_b, y_b, z_b) в пространстве:

AB = √(x_b - x_a)² + (y_b - y_a)² + (z_b - z_a)²

Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x_b - x_a; BC = y_b - y_a.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √AC² + BC².

2) Если точка М(x; y) лежит на прямой, проходящей через две данные точки ( , ) и ( , ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам

, . Если точка М является серединой отрезка , то ее координаты определяются по формулам , .

3) Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Полярными координатами произвольной точки М (относительно заданной системы) называются числа и (см. рис.). Угол при этом следует понимать так, как принято в тригонометрии. Число называется первой координатой, или полярным углом точки М ( называются также амплитудой).

Символ М( ; ) обозначает, что точка М имеет полярные координаты и .

Полярный угол имеет бесконечно много возможных значений (отличающихся друг от друга на величину вида , где n - целое положительное число). Значение полярного угла, удовлетворяющее неравенствам , называется главным.

В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1). Пользоваться одним и тем же масштабом, 2). При определении полярных углов считать положительным повороты в том направлении, в каком следует вращать положительную ось абсцисс, чтобы кратчайшим путем совместить ее с положительной осью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, то есть ось Ох направлена вправо, а ось Оу - вверх, то и отсчет полярных углов должен быть обычным, то есть положительными следует считать те углы, которые отсчитываются против часовой стрелки). При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки х к декартовым координатам той же точки осуществляется по формулам , . В этом же случае формулы , являются формулами перехода от декартовых координат к полярным.

При одновременно рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми.

4) Уравнение прямой – это уравнение, связывающее координаты x и y любой точки, лежащей на прямой.

Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к оси ОХ. Угловой коэффициент обозначается через k.

Итак, Итак, угловой коэффициент обозначается .

Если j- острый угол, то k>0, если j- тупой угол, то k<0, если j=0 прямая параллельна оси ОХ и k=0, если , то прямая не имеет углового коэффициента.

Напишем уравнение прямой, имеющей угловой коэффициент, равный k и отсекающей отрезок величины b на оси OY.

Пусть M(x,y)- произвольная точка прямой. Рассмотрим треугольник MBN; он прямоугольный. Очевидно, что

Значит , откуда получаем уравнение (1)

Это и есть уравнение прямой с угловым коэффициентом.

5) Уравнение прямой, проходящей через данную точку в данном направлении.

Дана точка , k – угловой коэффициент. Написать уравнение прямой, проходящей через точку и имеющей угловой коэффициент k.

Пусть M(x,y) – произвольная точка прямой. Рассмотрим треугольник M₁MN:

Откуда получаем искомое уравнение: (2)

6) Уравнение прямой, проходящей через 2 точки.

Пусть даны две точки и . Написать уравнение прямой, проходящей через эти точки.

Угловой коэффициент k определим из треугольника M₂M₁N:

Подставим полученное значение k в уравнение (2):

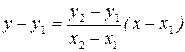
Разделим обе части уравнения на :

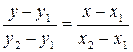
Запишем полученное уравнение в виде:

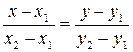(3)

Это и есть искомое уравнение прямой, проходящей через две точки.

7) Общее уравнение прямой.

Уравнение вида Ax+By+C=0 (4) называется общим уравнением прямой.

а). Пусть , тогда это уравнение можно записать в виде:

Это и есть уравнение прямой с угловым коэффициентом, т.е. уравнение

вида (1), где

Так как уравнение (1) есть уравнение прямой, то и уравнение (4) есть также уравнение прямой.

б). Если В=0, мы получаем . Это есть уравнение прямой, параллельной оси ОУ.