5. Представление логических формул в исчислении сильного включения схем направленных отношений.

Пусть – заданная логическая формула с множеством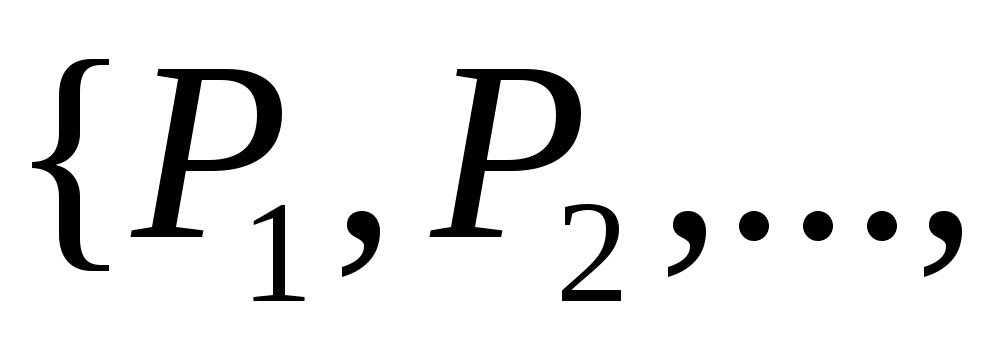свободных предикатных и функциональных переменных. Выполним первые четыре пункта процедуры приведения, подробно описанной в 3.3, и получим представление формулыв виде, где– введенные при скулемизации функциональные переменные,– связанные кванторами существования индивидные переменные, входящие хотя бы в одну из квазиэлементарных формул, которые могут быть одного из четырех видов:,,и, где– термы. Далее рассматривается только частьэтого представления, являющаяся формулой языка первого порядка. Если– модель формулы, то любое расширениеинтерпретациина множество функциональных переменныхявляется моделью формулы. Рассмотрим формулу, которая будет иметь вид, где– квазиэлементарные формулы, инверсные. Если– модель формулы, то для любого расширенияинтерпретациина множество функциональных переменных. Используя знак импликации, преобразуем полученную формулук виду, где всеи– элементарные формулы уже только одного из двух видов:или; если множество значенийили– пусто, то в посылке используется константа, а в следствии – константа.

Пусть – сетевые языки в некотором базисе, причем для всехиимеют одинаковую арность.

Определение 3.2. Система включений выполнима для реляционной интерпретации элементов базиса, если для всехимеют место включения.

Определение 3.3.Система включений общезначима, если она выполнима для любой реляционной интерпретации .

Определение 3.4.Система включений противоречива, если она не выполнима для любой реляционной интерпретации .

Построим теперь систему (конечное множество) «включений» сетевых языков: для всех, где– сеть – представление формулы(эквивалентной формуле), а– сети – представления формул(для всех). Правила построения этих представлений (отображенияи) для базисав графическом виде определены на рис. 3.1. Заметим, что все определяемые сети имеют одинаковую арность, где– количество связанных кванторами общности переменных, и представляют в интерпретации предикаты, аргументами которых являются переменные, а значения задаются соответствующими логическими формулами.

Пусть – интерпретация свободных предикатных и функциональных переменныхисходной логической формулы.

Теорема 3.3. является моделью исходной логической формулы, если и только если построенная для нее вышеописанным способом система включений сетевых языков не выполнима ни для какой согласованной с(см. определение 3.4) интерпретацииэлементов базиса.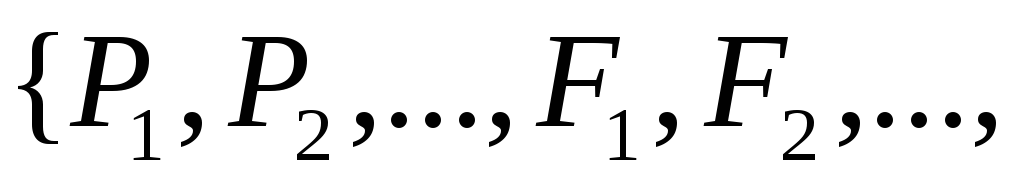

Теорема 3.4. Формула языка исчисления предикатов первого порядка с равенством общезначима, если и только если построенная для нее система включений противоречива.

6. Метод сетевой резолюции.

Эта раздел посвящен рассмотрению реализации логического вывода средствами теории направленных отношений на примере задачи доказательства общезначимости формул языка исчисления предикатов первого порядка с равенством и основана на результатах, изложенных в предыдущих разделах этой главы.

Используемый нами термин сетевая резолюция относится к процедуре вывода общезначимости формул языка исчисления предикатов первого порядка на базе сетевого представления схем направленных отношений. Основными отличиями сетевой резолюции от традиционного резолютивного логического вывода являются:

• базирующаяся на сетевом представлении схем -отношений техника проведения доказательства, в частности, выполнения тех действий, которые являются аналогом процедуры унификации;

• отказ при доказательстве от явного использования эрбрановской интерпретации и, вследствие этого, получение в ходе доказательства (возможно, не успешного!) в компактной сетевой форме функциональных уравнений, решения которых представляют собой модели рассматриваемой формулы при любых интерпретациях предикатных символов;

• использование прямого вывода истинности заданной формулы, а не доказательства тождественной ложности инверсной, что потребовало применения не традиционной, а двойственной формы скулемизации;

• применение специальной техники доказательства формул с равенством на базе сетевого представления схем -отношений;

• наконец, элиминация самой процедуры резолюции за счет использования рекурсивной подстановки на сетях, составляющей основу механизмов вычислений рекурсивных -отношений.

Как было показано в разделе 3.4, логическая формула, общезначимость которой требуется установить, может быть представлена конечным множеством сетейв базисес определенными ограничениями на интерпретацию элементов этого базиса. Эти ограничения отражают требования к возможным интерпретациям предикатных и функциональных переменных в логике первого порядка, и очевидно, что они могут быть выражены в форме сетевых эквивалентностей, показанных на рис. 3.2 (). Количество таких дополнительных эквивалентностей видаконечно в силу конечности базиса.

Общезначимость рассматриваемой логической формулы, очевидно, равносильна истинности утверждения

.

Т.к. , т.е. – график функции , а , то, согласно определению реляционной интерпретации для сетей, если длявыполняются гипотезы утверждения, то, когда – истинно и – в противном случае. Кванторы, требующие существования значений индивидных переменных, отражают условие существования фигурирующей в определении реляционной интерпретации сетифункции разметки.

Отсюда следует справедливость следующей теоремы:

Теорема 3.5. Задача установления общезначимости формулы языка исчисления первого порядка с равенством сводится к проблеме выводимости из гипотез равенства¹ в исчислении сильной реляционной эквивалентности конечных множеств сетей (конечных сетевых языков).

Рассмотрим процесс направленного применения эквивалентных преобразований, формализующих свойства функциональности и тотальности элементов базиса (см. рис.3.2и рис.3.2). Замена в любой из сетей, входящей в рассматриваемое множество (в начальный момент это множество), фрагмента вида левой части эквивалентности на фрагмент вида правой части приводит к упрощению этой сети, т.к. в нейуменьшается количество элементов, и, следовательно, эти преобразования отвечают условию нетеровости. Аналогичным образом обстоит дело и с преобразованиями, вытекающими из ортогональности интерпретаций элементов базиса и, представляющих некоторую предикатную переменную. Вхождение с одинаковыми входными точками пары элементов таких сортов в одну сеть (рис. 3.2) означает, что для любой допустимой интерпретации вся эта сеть представляет пустое отношение и, следовательно, она может быть исключена из рассматриваемого множества сетей. При этом такое преобразование множества сетей тоже является упрощающим, т.к.уменьшает мощность рассматриваемого множества сетей и, вследствие этого, имеет свойство нетеровости.

Помимо указанных преобразований, мы можем использовать сохраняющие реляционную интерпретацию преобразования общего вида: , если, т.е. для любой интерпретации элементов базиса. Известны два общего вида способа получения всех такихдля– включение вновых элементов и отождествление точек в сети. Если целью преобразования является получение в множестве сетей (напомним, что все сети – арности) пустой сети, представляющей истинностное значение, то первое преобразование бесполезно. В лучшем случае в процессе дальнейших преобразований эти новые элементы будут удалены из сетей, в которые они были добавлены, но наличие этих новых элементов не может иметь следствием удаление других элементов. Отождествление же точек может в некоторых случаях привести к возможности выполнения новых упрощающих преобразований и поэтому может быть использовано при доказательстве нашего утверждения. При этом важно, что отождествление точек не лишает всю систему свойства нетеровости, т.к. его осуществление хотя и приводит к появлению новой сети в рассматриваемом множестве, но эта сеть является более простой (в нейменьше точек при одинаковых других условиях) по отношению к сети, уже имеющейся в рассматриваемом множестве. Однако разнообразие случаев применения этого преобразования может и должно быть существенно ограничено. Во-первых, чтобы возникла возможность применения преобразования, связанного со свойством функциональности, отождествляемые точки должны быть одинаковыми по номеру входными точками элементов одного и того же сорта. Во-вторых, т.к. только преобразование, связанное с тотальностью, может привести к уменьшению количества различных сортов элементов в сети, то достаточно применять отождествление входных точек элементов одного сорта только тогда, когда эти элементы имеют общую выходную точку. В силу того, что выделенный случай отождествления точек при преобразовании вгарантирует эквивалентностьтолько тогда, когда связанный с этим преобразованием сорт элементов интерпретируется как конструктор (что, согласно определению допустимых интерпретаций логического языка первого порядка, конечно, не является обязательным), то исходная сетьтоже должна остаться в рассматриваемом множестве сетей.

Наконец, равносильное свойству дополнительности сортов иэлементов сетей требование к предикатам, чтобы они, как это предполагается при интерпретации предикатных переменных в логическом языке первого порядка, были всюду определены на, может быть выражено в форме сетевой эквивалентности так, как показано на рис. 3.2. Это ограничение на интерпретацию предикатных символов находит отражение в известной теореме

,

реализуемой в теории доказательств в форме так называемого правила резолюции (мы приводим здесь только одну из двух двойственных формулировок правила резолюции):

Новый дизъюнктивный член называется резольвентой двух исходных.

Для сетевого представления логических формул в теории направленных отношений это правило имеет вид, показанный на рис. 3.3. Его справедливость нетрудно показать следующим образом. Пусть и– сорта элементов, интерпретируемые как ортогональные и дополнительные направленные отношения арности. Тогда для любой интерпретациитерминального базиса

и

,

т.к. сети в левых частях получены добавлением новых элементов к сетям в правых частях включений. Здесь – элементарные одноэлементные сети с элементами сортови. Объединяя левые и правые части, получим



и далее, используя дистрибутивность объединения относительно операции последовательной композиции, получим

,

.

Отсюда непосредственно следует приведенное выше правило сетевой резолюции.

Заметим теперь, что резольвентаможет быть получена как результат подстановки сетив сетьвместо элемента сортаили подстановкой сетив сетьвместо элемента сорта(рис. 3.4).

Это позволяет сделать равносильное для доказательства преобразование представляющего рассматриваемую логическую формулу множества сетей арностив сетевой язык, индуцированный сетевой грамматикой, где терминальный базис, нетерминальный базис, аксиома– новый нетерминальный сорт арности, а правилаимеют вид:

…,

для всех и, таких, что,

для всех и, таких, что.

Заметим, что если ни одна из сетей в отдельности не редуцируема к пустой сети, то в качестве правил для аксиомы грамматики можно взять правила… .

Определим теперь общую идею построения процедуры доказательства утверждения .

Построим сетевую КС-грамматику описанным выше способом. Очевидно, что порождаемый ею язык эквивалентен в интерпретации исходному множеству сетей : по построению грамматики он, с одной стороны, включает все, а, с другой стороны, все порождаемые подстановками сети (фактически, резольвенты) не расширяют интерпретацию.

Рассмотрим вариант базового языка исчисления предикатов первого порядка (без равенства), т.е. случай, когда среди квазиэлементарных формул нет формул вида .

Для всякой сети в терминальном (теперь чисто функциональном) базисе можно утверждать, что либо она трансформируется (редуцируется) к нормальной форме рассмотренными выше преобразованиями, либо будет доказано, что она имеет пустую интерпретацию при любой интерпретации элементов терминального базиса. Можно показать, что

1. интерпретация любого конечного множества непустых сетей в нормальной форме пуста для некоторой удовлетворяющей необходимым требованиям интерпретации элементов базиса и

2. это же свойство сохраняется и для любого рекурсивно-перечислимого множества сетей в нормальной форме, не содержащего пустую сеть . Следовательно, доказываемое утверждение истинно тогда и только тогда, когда в порождаемый язык входит сеть, редуцируемая к пустой сети, также являющейся сетью в нормальной форме. Таким образом, проблема является полуразрешимой – множество сетей, порождаемых сетевой КС-грамматикой, рекурсивно-перечислимо, а система правил редукции имеет свойство нетеровости, т.е. любая сеть приводима к нормальной форме за конечное число шагов.

Теорема 3.6. Если исходное множество сетей реляционно эквивалентно (в сильном смысле) сети , то сетьбудет получена в результате редукции одной из сетей языка, порожденного описанной выше сетевой КС-грамматикой.

В качестве основы процедуры доказательства можно взять любую корректную процедуру порождения языка по сетевой КС-грамматике. Если это – процедура дедуктивного вида, то, исходя из особенностей задачи, имеется немало возможностей существенного сокращения числа вариантов вывода сетей из аксиомы грамматики. Рассмотрим некоторые из этих ситуаций.

1. Если в сети (здесь и далее, возможно, содержащей нетерминальные элементы) обнаружен фрагмент (подсеть) вида рис. 3.2, то такая сеть исключается из множества выводимых из аксиомы сетей.

Описываемые далее ситуации 2 и 3 справедливы только для чистого языка исчисления предикатов первого порядка без равенства – в этом случае среди квазиэлементарных формул в оконечном представлении рассматриваемой формулы не будет неравенств вида и, следовательно, при доказательстве не выполняется каким-то особым образом резолюция по равенству.

2. Если в сети имеется цикл (из элементов терминальных сортов, т.к. нетерминальные сорта имеют арностьи, таким образом, не могут входить в циклы), то цикл не может быть устранен в любой порожденной сети в процессе рекурсивного вывода из аксиомы и при дальнейшей редукции. Сеть с циклом, следовательно, не может привести к порождению пустой сетии без ущерба для целей нашего доказательства может быть исключена из процесса вывода. Циклом мы называем фрагмент сети вида, показанного на рис.3.5.

3. Если в сети имеется точка, являющаяся одновременно выходной точкой двух элементов различных терминальных сортов, то эта ситуация сохраняется во всех порождаемых из этой сети сетях и, следовательно, тоже не может привести к порождению пустой сети и подлежит исключению из процесса вывода.

4. Наиболее сложной в реализации является проверка для каждой новой выведенной сети включениядля любой из ранее выведенных сетей, хотя, если это будет установлено (это отношение между сетями предполагает включение интерпретаций при любой интерпретации элементов базиса), томожет не включаться в число выводимых из аксиомы сетей. Проблема состоит в том, что эта проверка может оказаться более трудоемкой, нежели избыточное продолжение вывода и для.