3. Сетевой логический вывод

3. Сетевой логический вывод

1. Введение.

Часть 3 цикла работ по теории направленных отношений посвящена изложению результатов, раскрывающих взаимосвязь теории направленных отношений и логики, прежде всего, логики первого порядка с равенством, на подмножестве которой – логике «хорновских» дизъюнктов – базируются многие языки логического программирования, в том числе Пролог.

Как уже отмечалось в части 1, многие виды семантических объектов в конструктивной математике вообще и в математической логике, в частности, могут рассматриваться как специальные подклассы -отношений, различающиеся как арностью, так и наличием у этих -отношений особых свойств. В качестве основных таких свойств выступают тотальность и функциональность -отношений, введенные в разделе 1.1 и более подробно рассмотренные в главе 2.

Для того, чтобы представить себе возможные применения теории направленных отношений для решения задач, традиционно относящихся к приложениям математической логики, достаточно вспомнить, что существуют всего два логических -отношения арности: пустое (пустое подмножество пар пустых кортежей) и– множество, содержащее единственный элемент (пару пустых кортежей), которые в основных приложениях теории направленных отношений играют роль истинностных значений и , соответственно.

Используемое нами определение языка исчисления предикатов (с равенством) дано в разделе 3.2 и согласовано по стилю с определением языков схем -отношений. Нетрудно видеть, что все необходимые для определения интерпретации логических формул семантические объекты также могут быть представлены в терминах теории направленных отношений. Последующие разделы этой главы посвящены проблеме взаимной трансляции логических формул первого порядка и схем -отношений, а в разделах 3.7 - 3.9 рассматриваются механизмы логического вывода, реализованные средствами предлагаемой теории, причем для задания схем-отношений, как правило, будет использоваться их сетевое представление (глава 2).

2. Язык исчисления предикатов первого порядка с равенством.

В отличие от большинства известных формулировок, в определении языка исчисления предикатов первого порядка мы отказываемся от понятия константа, полагая, что роль констант могут играть нульарные связки, а также связанные кванторами существования нульарные функциональные и предикатные переменные. При теоретическом рассмотрении будем использовать более «экономную» префиксную нотацию, а в примерах – общепринятую функциональную нотацию для термов и вызовов предикатов.

В общем случае, в сигнатуру языка исчисления предикатов первого порядка с равенством входят:

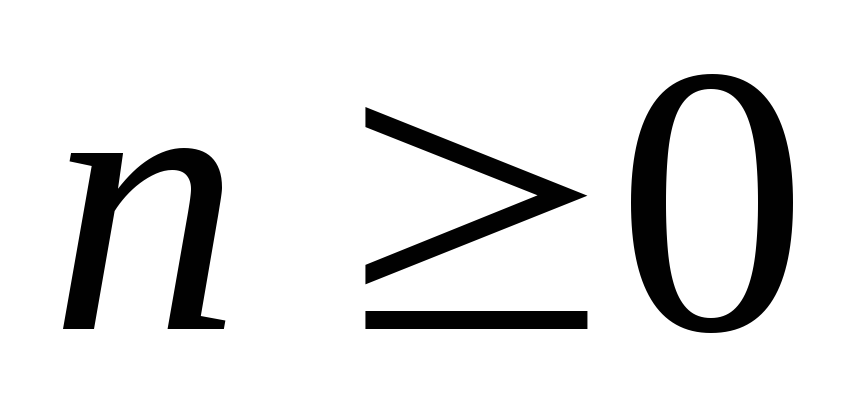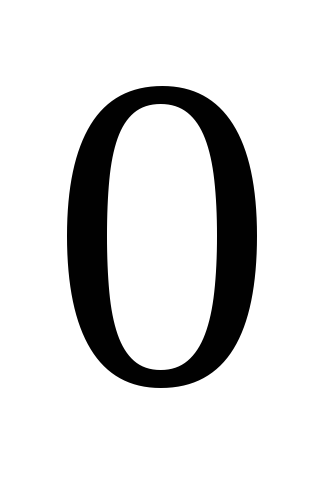• неограниченное (счетное) количество символов предикатных переменных любых арностей ; предикатные переменные арностиназываютсялогическими (пропозициональными) переменными;

• неограниченное количество символов функциональных переменных любых арностей 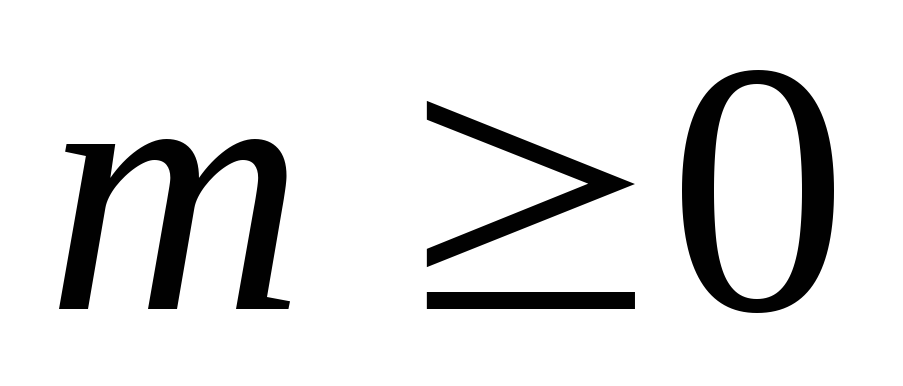; функциональные переменные арностиназываютсяиндивидными переменными;

• связки для обозначения логических функций произвольных арностей, присоединенные функции которых образуют полную систему логических функций; связки арности 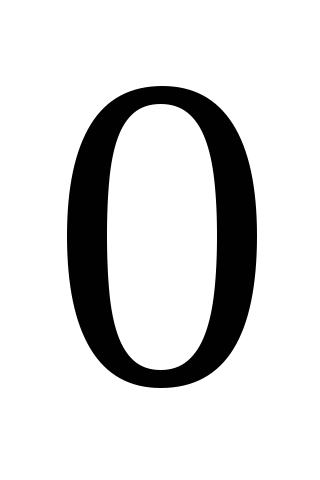называются логическими константами;

• связка «» для обозначения предиката равенства;

• унарно-унарные операторы – кванторы общности и существования, применимые в языках первого порядка к логическим формулам (далее – просто к формулам) только по индивидным и пропозициональным переменным.

Термом называется конструкция вида , где–-арная функциональная переменная,, а– термы. В частности, отдельно взятая индивидная переменная является термом.

Элементарная формула это либо – результат применения связки равенства к термами, либо конструкция, где–-арная предикатная переменная,, а – термы. В частности, отдельно взятая пропозициональная переменная является элементарной формулой.

Формула – либо элементарная формула, либо результат применения -арной логической связки к формулам, , либо одна из конструкцийили– результатов применения кванторов общности и существования к формулепо индивидной или пропозициональной переменной.

Далее будем придерживаться следующих соглашений:

1) для обозначения связанных (операторных) переменных будем использовать строчные буквы, возможно, с индексами: – для индивидных и– для пропозициональных;

2) для обозначения свободных переменных будем использовать заглавные буквы, возможно, с индексами: – для функциональных и– для предикатных;

3) самые внешние и группирующие скобки при применении логических связок могут быть частично опущены согласно приоритетам этих связок (перечислим некоторые из них их в порядке убывания приоритета: (отрицание) и кванторы, (конъюнкция),  (импликация),  (дизъюнкция),  (логическая эквивалентность)).

Пусть – универсум и– произвольная допустимая интерпретация переменных: для всякой функциональной переменной -всюду определенная на -арная функция, для всякой предикатной переменной – всюду определенный на -арный предикат. Истинностная интерпретация всякой формулы определяется общепринятым образом. обозначает интерпретацию формулы при интерпретациипеременных. Очевидно, что интерпретация всякой формулы зависит только от интерпретации ее свободных переменных.

Интерпретация свободных переменных формулыназывается еемоделью, если . Формуланазываетсяобщезначимой, если любая допустимая интерпретация свободных переменных формулыявляется ее моделью. Формуланазываетсявыполнимой, если она имеет хотя бы одну модель. Формула называетсяпротиворечием, если не имеет моделей. Формула называетсяопровергаемой, если она не является общезначимой (то есть если существует хотя бы одна интерпретация , не являющаяся моделью формулы).