- •2 . Сетевые языки функционального и логического программирования
- •Сетевые языки функционального и логического программирования
- •Графические представления схем -отношений.
- •Базисы и сети.
- •Элементарные сети.
- •Операции композиции сетей.
- •Свободные и связанные сети. Вложение сетей.
- •Сетевые языки.
- •Сетевая интерпретация рекурсивных схем -отношений.
- •Реляционная интерпретация сетевых языков.
- •Примеры задания сетевых языков и их реляционной интерпретации.
- •Формализация отношений реляционного включения и эквивалентности сетевых языков.
- •Литература
- •Оглавление
- •41 F logol:язык и система функционально-логического программирования
Сетевая интерпретация рекурсивных схем -отношений.
Пусть
![]() – рекурсивная схема
– рекурсивная схема![]() -отношений.
Преобразуем ее к эквивалентной форме
задания в виде конечной системы уравнений
вида
-отношений.
Преобразуем ее к эквивалентной форме
задания в виде конечной системы уравнений
вида
![]()
![]() ,
такой, что
,
такой, что
для всех
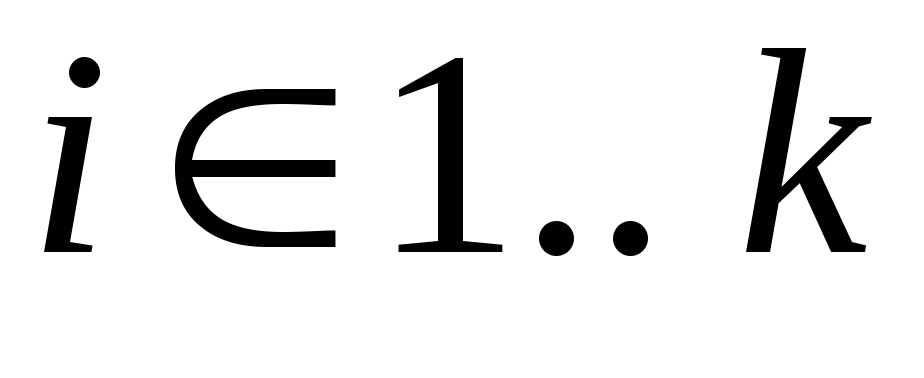 переменные
переменные Используя дистрибутивность объединения
относительно операций последовательной
и параллельной композиции, преобразуем
все
Используя дистрибутивность объединения
относительно операций последовательной
и параллельной композиции, преобразуем
все
 ,
,
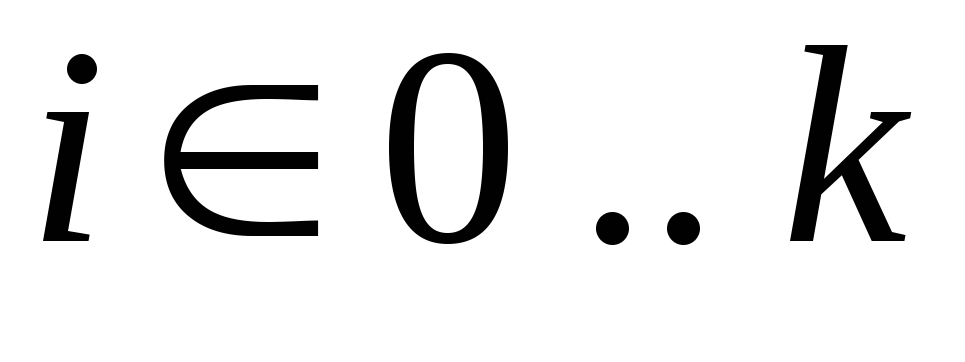 ,
к виду
,
к виду
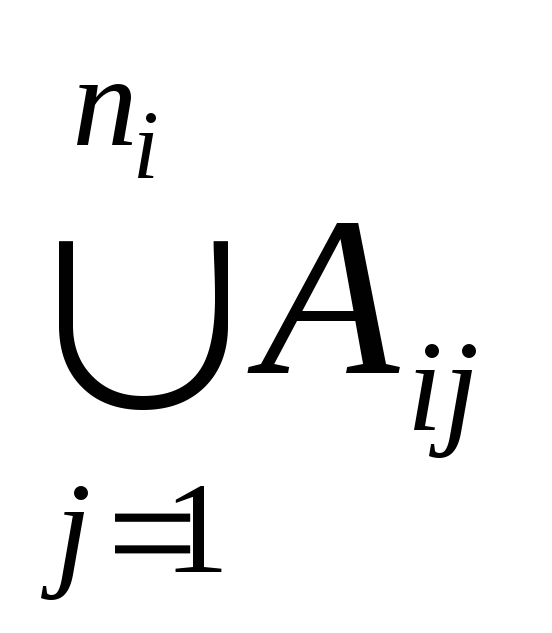 ,
где все
,
где все
 – простые схемы
– простые схемы
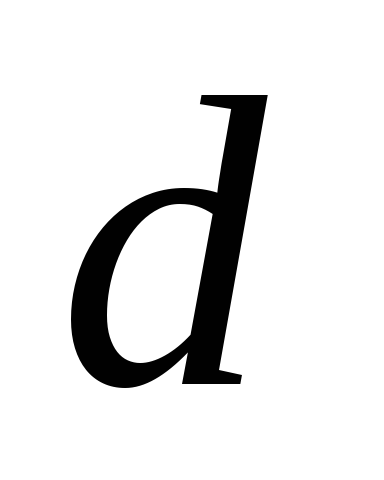 -отношений,
т.е. в них не используются операция
объединения и оператор рекурсии;
-отношений,
т.е. в них не используются операция
объединения и оператор рекурсии;
для любой интерпретации
 свободных переменных
свободных переменных

– первый компонент кортежа – минимального
решения этой системы уравнений в
интерпретации
– первый компонент кортежа – минимального
решения этой системы уравнений в
интерпретации
 .
.
Сетевая
интерпретация
![]() рекурсивных схем определяется так:
рекурсивных схем определяется так:
Определение
2.16.
![]()
![]()
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
Полезной, но не обязательной, является последующая “чистка” нетерминального базиса.
Пусть
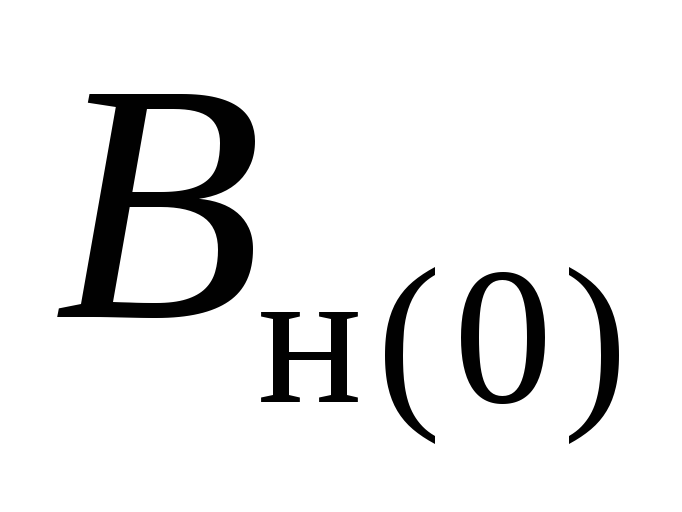 – пустое подмножество
– пустое подмножество .
Вычислим предел
.
Вычислим предел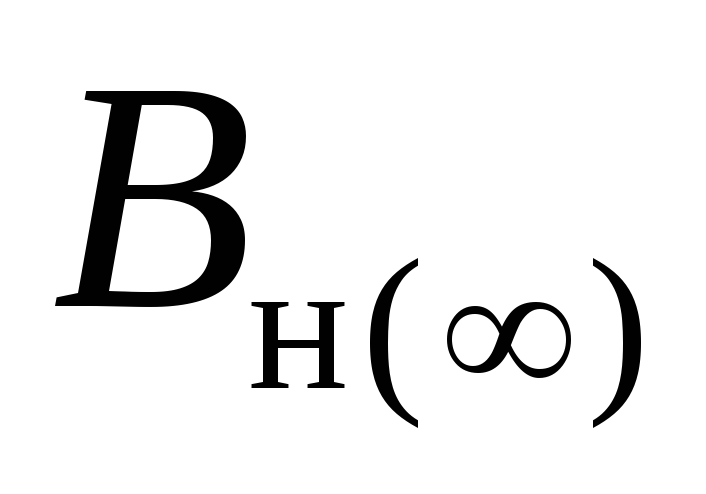 (его существование очевидно)
последовательности
(его существование очевидно)
последовательности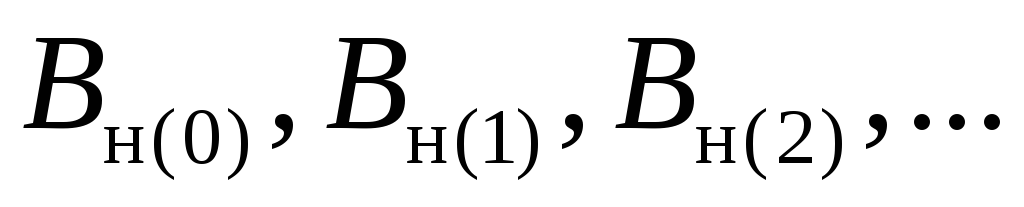 где
где
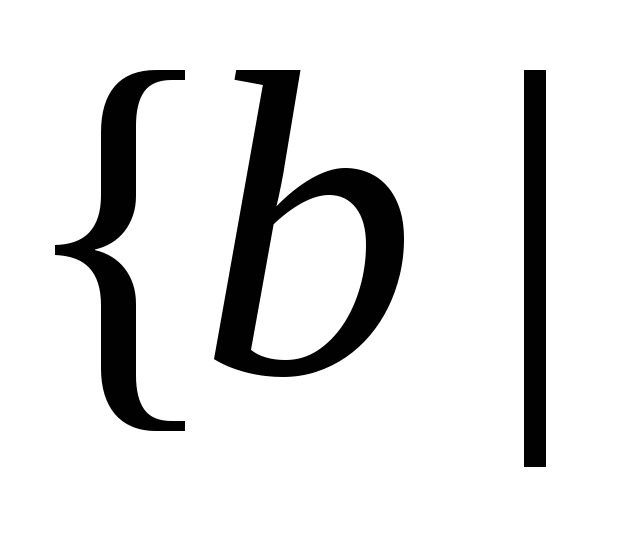 существует
правило
существует
правило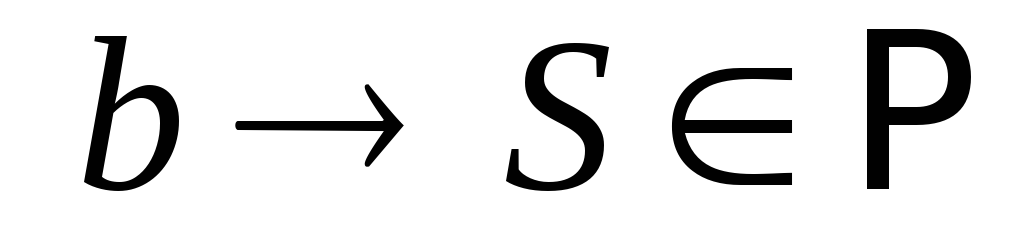 ,
такое, что все элементы сети
,
такое, что все элементы сети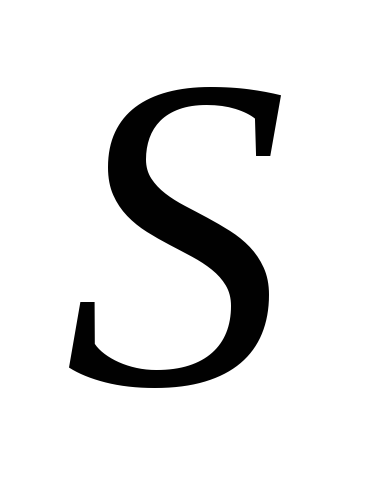 нетерминальных сортов являются
элементами сортов из
нетерминальных сортов являются
элементами сортов из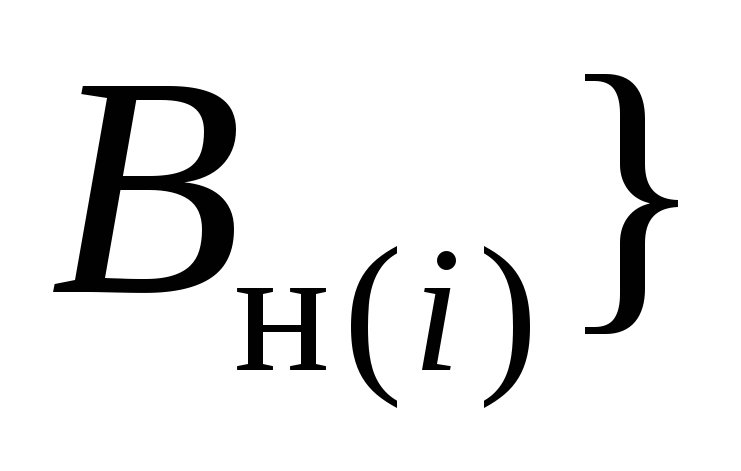 .
Если
.
Если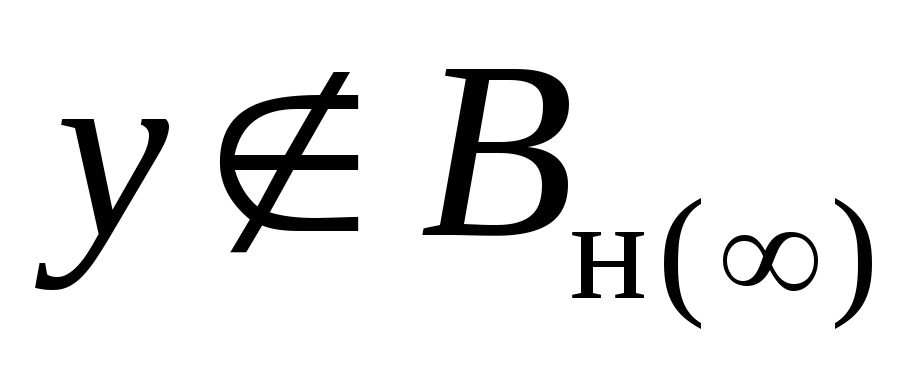 (
(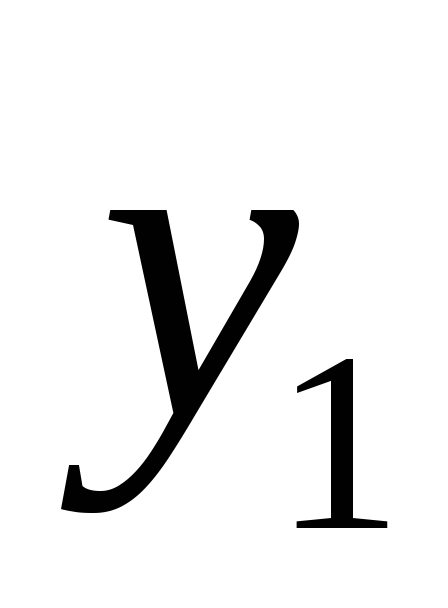 – аксиома грамматики), то
– аксиома грамматики), то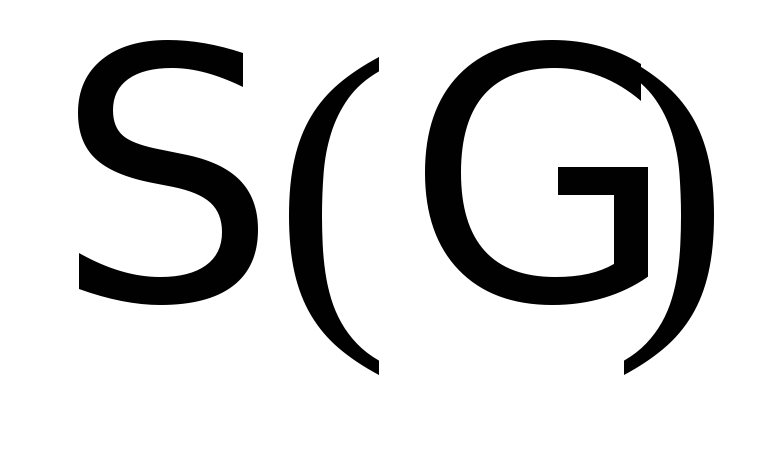 – пустой язык, в противном случае в
множестве правил
– пустой язык, в противном случае в
множестве правил оставим только те из них, в которых
используются исключительно сорта из
оставим только те из них, в которых
используются исключительно сорта из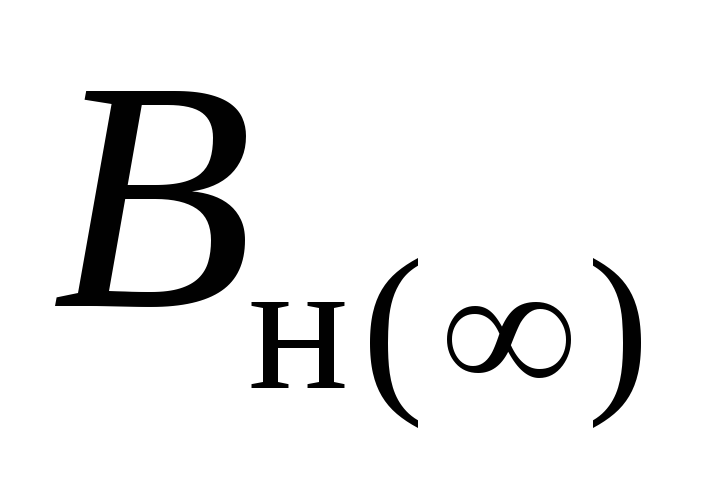 .
.Пусть
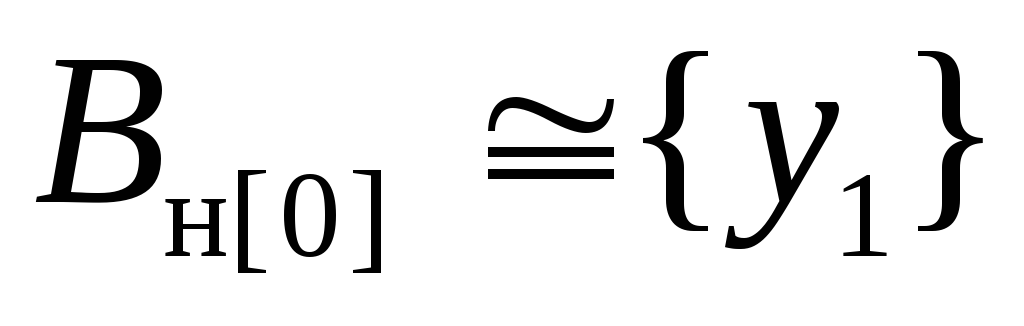 .
В качестве нового нетерминального
базиса возьмем предел последовательности
.
В качестве нового нетерминального
базиса возьмем предел последовательности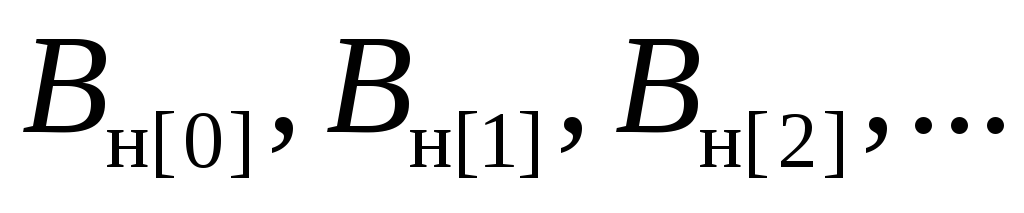 ,
где
,
где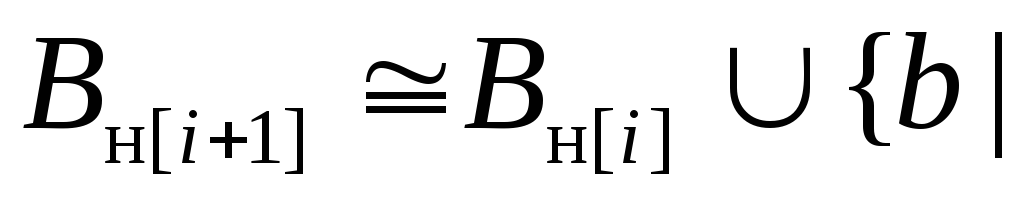 существует правило
существует правило такое, что сеть
такое, что сеть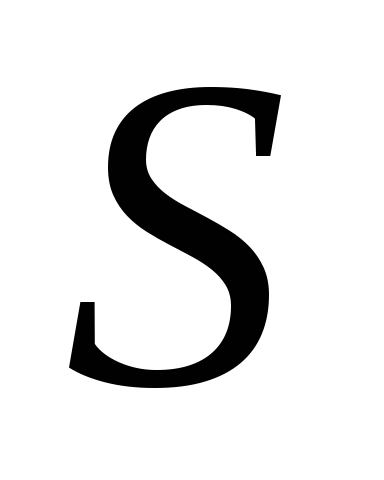 содержит
элемент сорта из
содержит
элемент сорта из
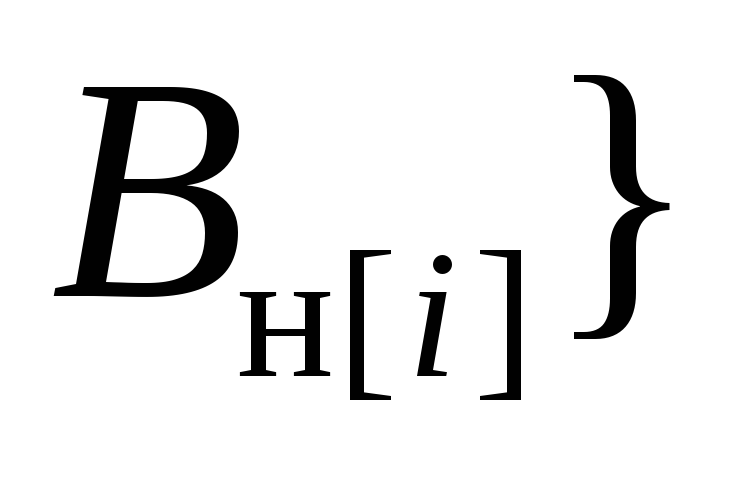 .
В множестве правил снова оставим только
те правила, в которых используются
исключительно сорта из построенного
множества. Таким образом, в нетерминальном
базисе останутся только те нетерминальные
символы, которые «нужны» для определения
аксиомы
.
В множестве правил снова оставим только
те правила, в которых используются
исключительно сорта из построенного
множества. Таким образом, в нетерминальном
базисе останутся только те нетерминальные
символы, которые «нужны» для определения
аксиомы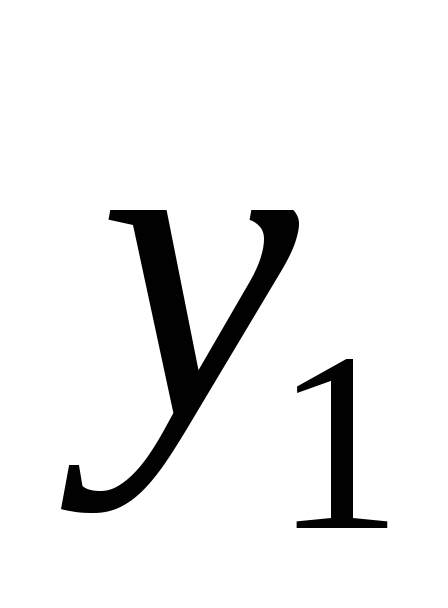 .
.
Реляционная интерпретация сетевых языков.
Пусть
![]() – сетевой язык в базисе
– сетевой язык в базисе![]() ,
заданный КС-грамматикой
,
заданный КС-грамматикой![]() .
Фиксируем интерпретацию
.
Фиксируем интерпретацию![]() элементов терминального базиса
элементов терминального базиса![]() так, что для всех
так, что для всех![]()
![]() ¤
¤![]() ¥
–
¥
–
![]() -отношение
арности
-отношение
арности
![]() на носителе
на носителе![]() .
.
Определение
2.17. Интерпретация
![]() ¤
¤![]() ¥
сетевого языка
¥
сетевого языка
![]() ,
индуцированная интерпретацией
,
индуцированная интерпретацией![]() элементов терминального базиса, есть
элементов терминального базиса, есть
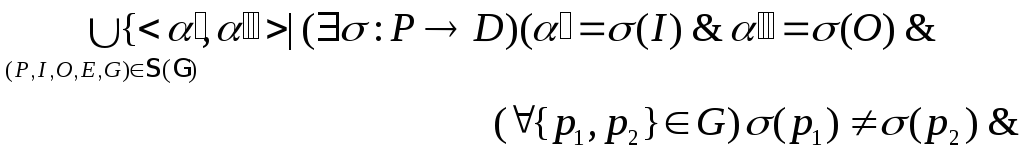
![]() ¤
¤![]() ¥
¥![]() .
.
Функция
![]() называетсяразметкой
точек сети; допустимые разметки должны
удовлетворять требованиям, предъявляемым
к точкам элементами сети и ее
называетсяразметкой
точек сети; допустимые разметки должны
удовлетворять требованиям, предъявляемым
к точкам элементами сети и ее
![]() -графом.
Пары кортежей допустимых разметок
входных и выходных точек сети являются
элементами определяемого
-графом.
Пары кортежей допустимых разметок
входных и выходных точек сети являются
элементами определяемого![]() -отношения.
-отношения.
Теорема
2.4.
![]() ¤
¤![]() ¥=
¥=![]() ¤
¤![]() ¤
¤![]() ¥¥
для всех
¥¥
для всех
![]() и
для всех интерпретаций
и
для всех интерпретаций
![]() .
.
Отсюда
следует важный вывод: сетевые
КС-грамматики могут рассматриваться
как форма задания рекурсивных схем
![]() -отношений.
-отношений.
В
заключение покажем, как для заданного
сетевого языка
![]() построить сетевой язык
построить сетевой язык![]() ,
такой, что для любой интерпретации
,
такой, что для любой интерпретации![]()
![]() ¤
¤![]() ¥
представляет
¥
представляет
![]() -отношение,
обратное
-отношение,
обратное
![]() -отношению
-отношению
![]() ¤
¤![]() ¥.
Пусть
¥.
Пусть
![]() -
арность языка
-
арность языка![]() .
Для построения грамматики
.
Для построения грамматики![]() языка
языка![]() по заданной грамматике
по заданной грамматике![]() языка
языка![]() нужно:
нужно:
изменить арность аксиомы
 грамматики
грамматики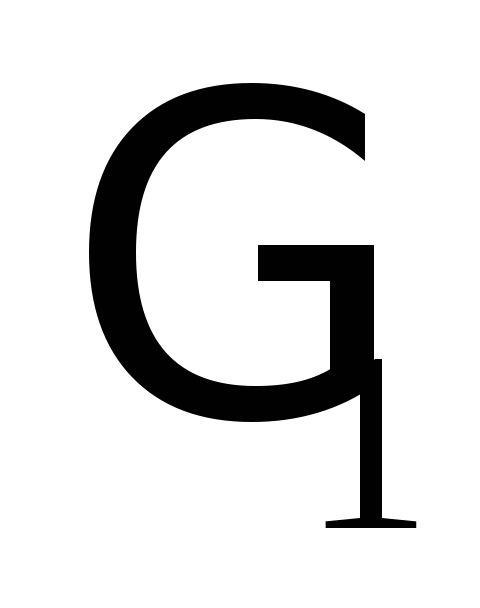 на
на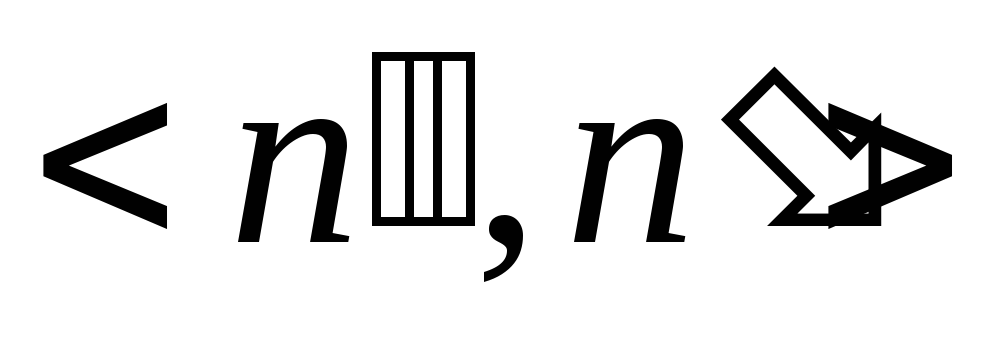 ;
;во всех правилах вида
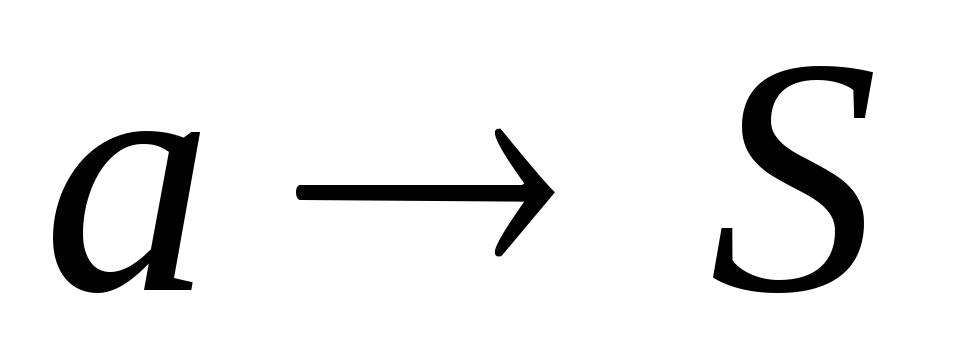 в сети
в сети
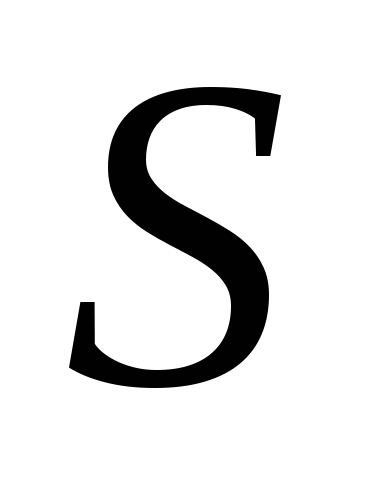 поменять местами кортежи входных и
выходных точек;
поменять местами кортежи входных и
выходных точек;все элементы сетей (правых частей всех правил) вида
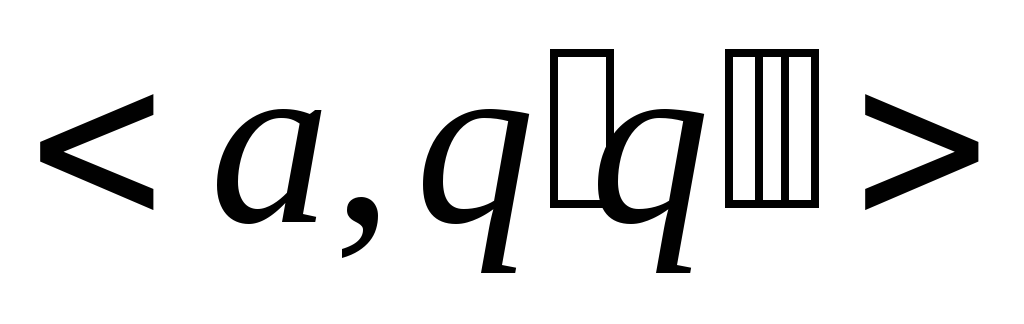 заменить на элементы
заменить на элементы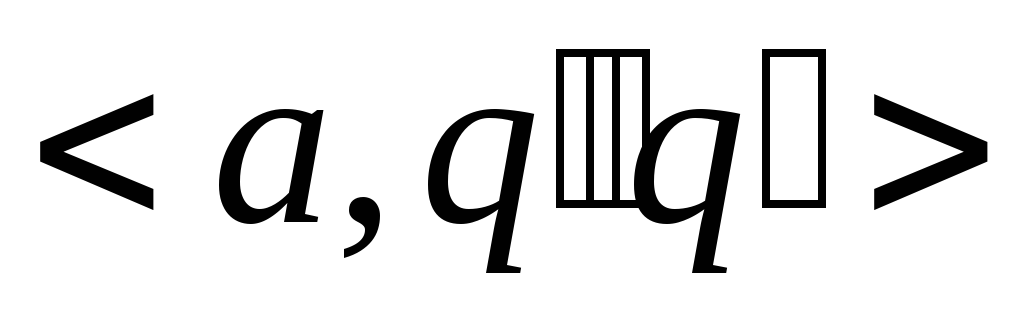 .
.
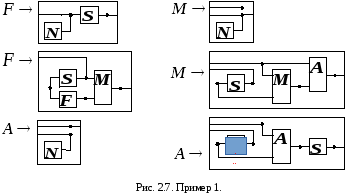
Примеры задания сетевых языков и их реляционной интерпретации.
Пусть
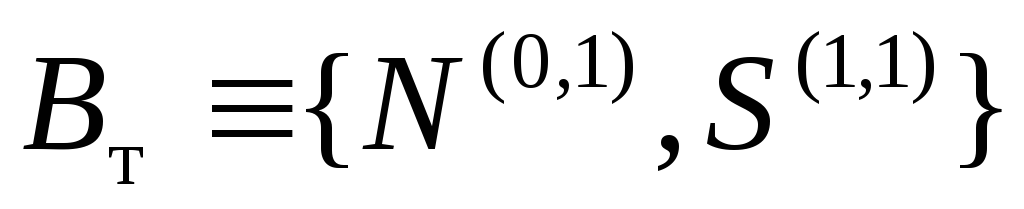 и задана сетевая грамматика
и задана сетевая грамматика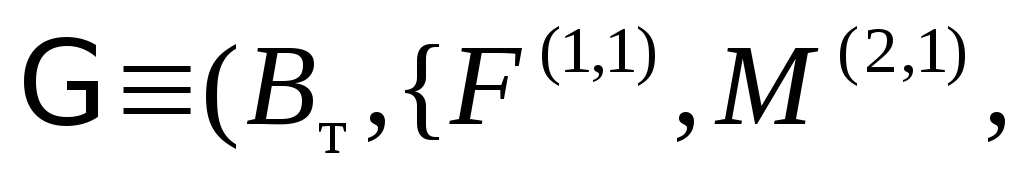
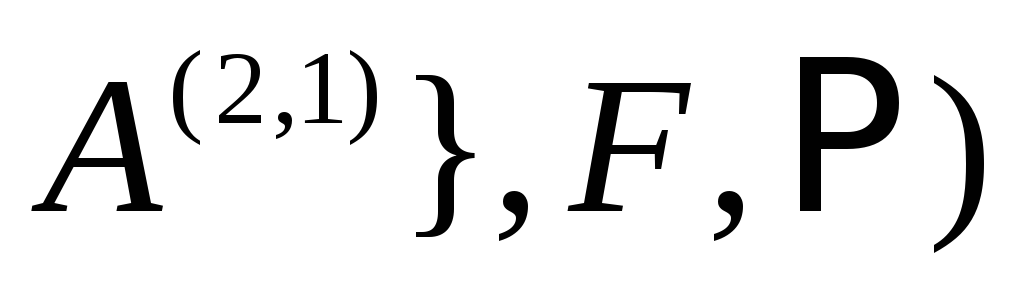 ,
где правила грамматики P показаны на
рис. 2.7.
,
где правила грамматики P показаны на
рис. 2.7.
Тогда
при
![]() ¤
¤![]() ¥
¥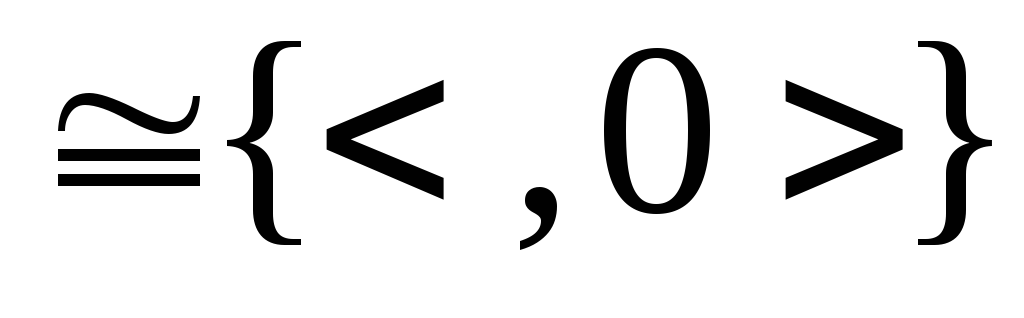 ,
,![]() ¤
¤![]() ¥
¥![]()
![]() ¤
¤![]() ¥
¥
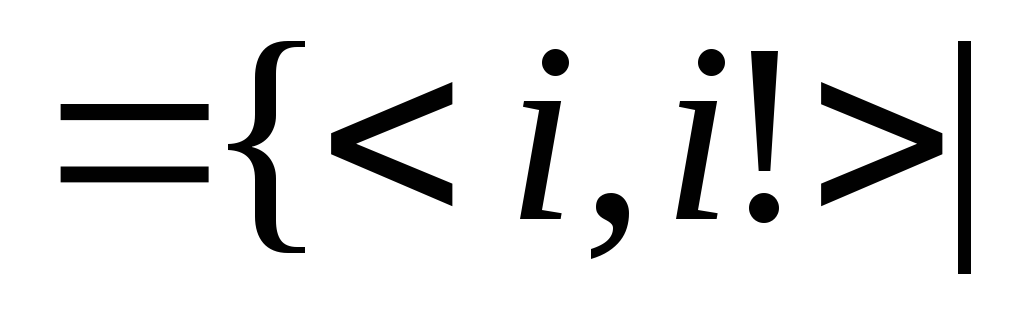
![]() ,
т.е. является графиком функции «факториал».
Нетерминальные сорта
,
т.е. является графиком функции «факториал».
Нетерминальные сорта![]() и
и![]() интерпретируются при этом как сложение
и умножение, соответственно.
интерпретируются при этом как сложение
и умножение, соответственно.
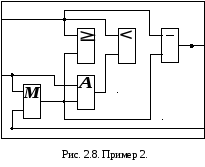
На рис. 2.8 изображена сеть
 ,
для которой
,
для которой ¤
¤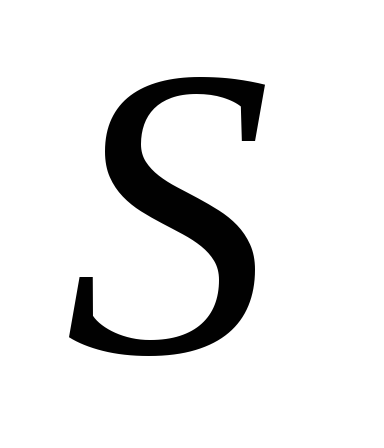 ¥
¥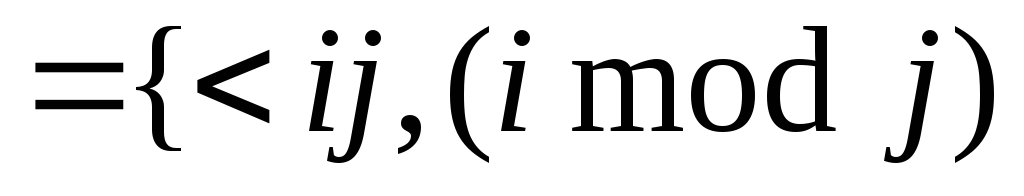
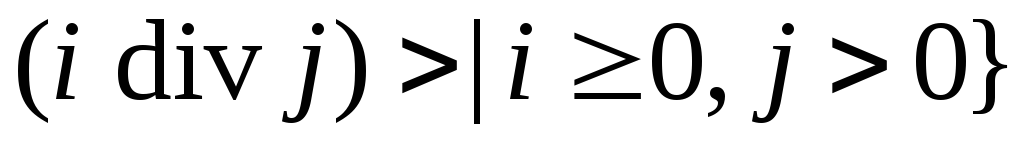 ,
при следующей интерпретации
,
при следующей интерпретации сортов ее элементов на множестве
натуральных чисел:
сортов ее элементов на множестве
натуральных чисел: ¤
¤ ¥
¥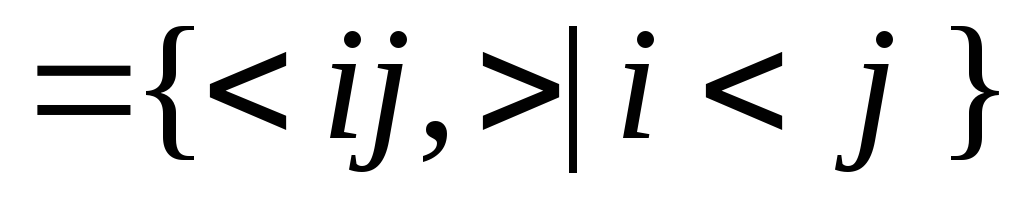 ,
, ¤
¤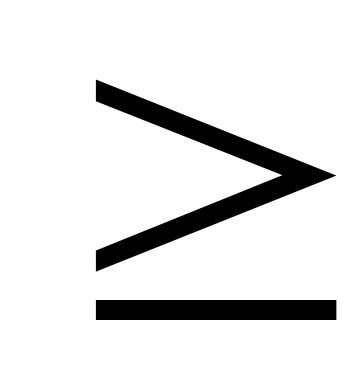 ¥
¥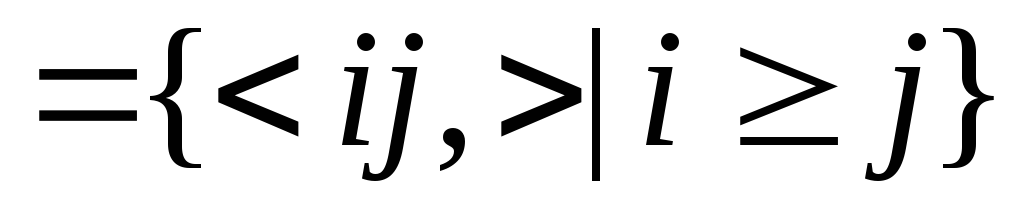 ,
, ¤-¥
¤-¥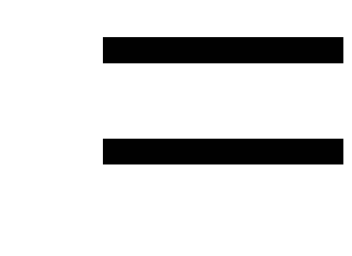
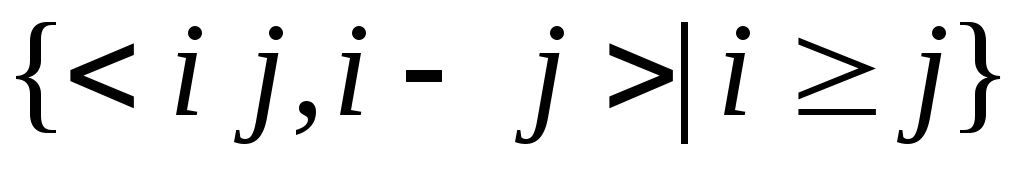 ,
, ¤
¤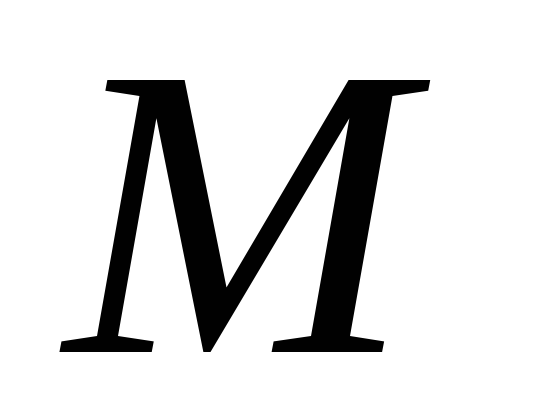 ¥
¥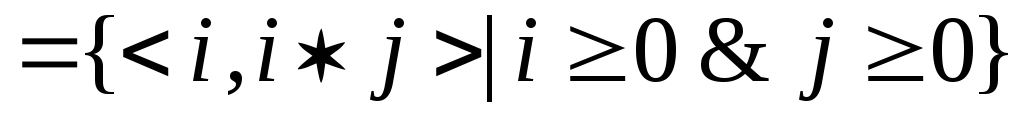 ,
, ¤
¤ ¥
¥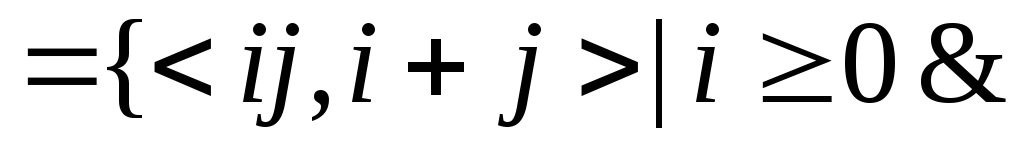
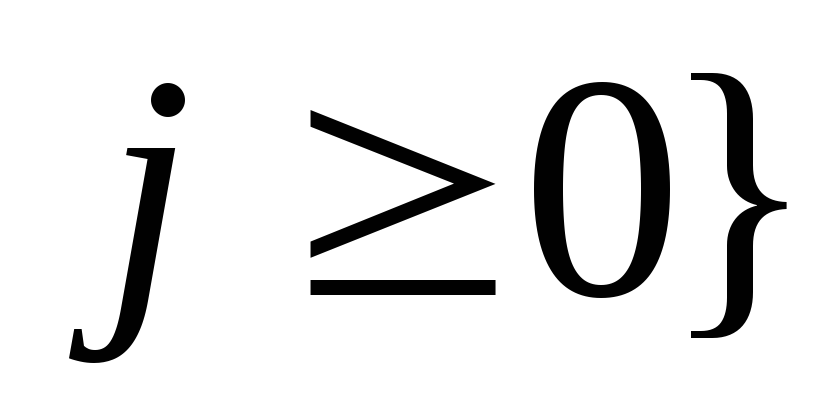
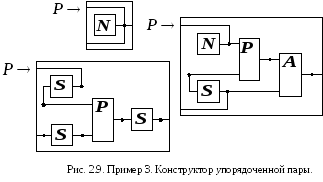
На рис. 2.9 представлены правила сетевой грамматики, определяющей конструктор
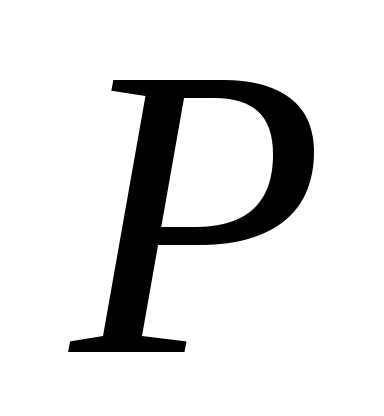 упорядоченной пары натуральных чисел
в базисе
упорядоченной пары натуральных чисел
в базисе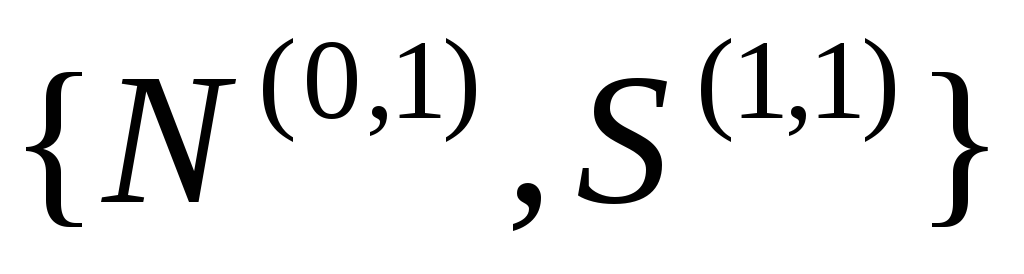 ,
интерпретация элементов которого дана
в предыдущем примере, на основе
«диагонального» метода нумерации.
,
интерпретация элементов которого дана
в предыдущем примере, на основе
«диагонального» метода нумерации.Рис. 2.10 представляет правила сетевой грамматики в терминальном базисе
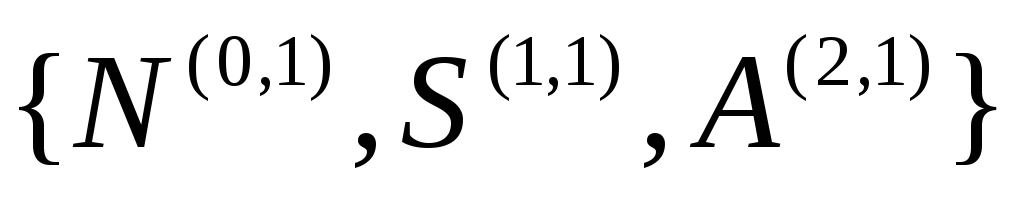 .
При интерпретации элементов базиса
как нуля, конструктора следующего числа
и сложения, соответственно, нетерминальный
сорт
.
При интерпретации элементов базиса
как нуля, конструктора следующего числа
и сложения, соответственно, нетерминальный
сорт интерпретируется как функция числа
сочетаний.
интерпретируется как функция числа
сочетаний.Правила сетевой грамматики, показанные на рис. 2.11, определяют операцию
 сцепления двух списков при интерпретации
сорта
сцепления двух списков при интерпретации
сорта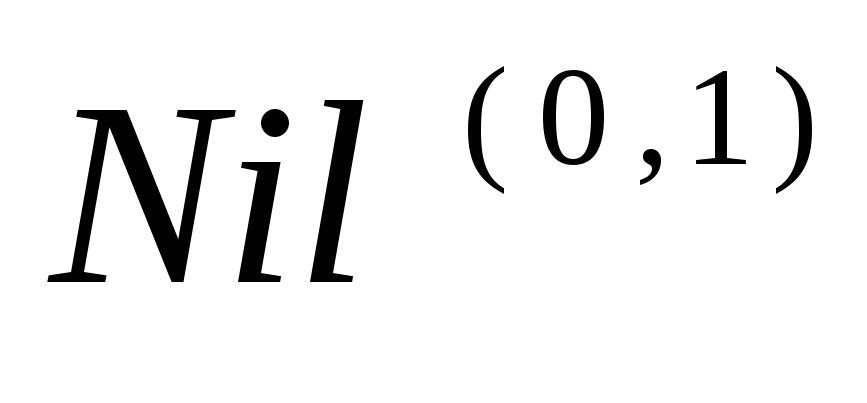 как конструктора пустого списка, а
как конструктора пустого списка, а – как конструктора двоичного
упорядоченного дерева (
– как конструктора двоичного
упорядоченного дерева (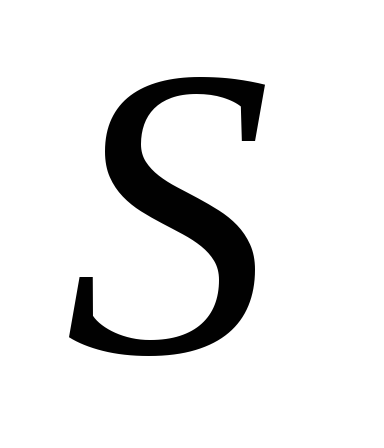 -операции
по Мак-Карти).
-операции
по Мак-Карти).На рис. 2.12 приведены правила сетевой грамматики в терминальном базисе
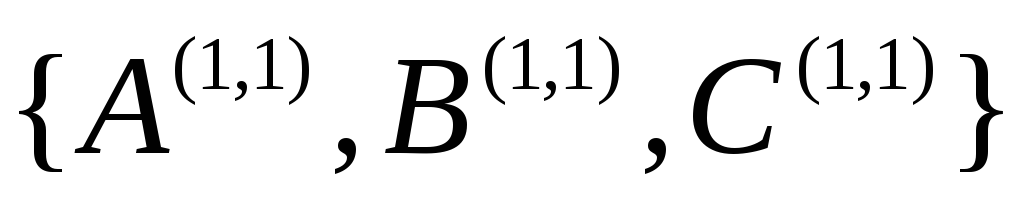 ,
сетевой язык которой представляет
(для нетерминального сорта
,
сетевой язык которой представляет
(для нетерминального сорта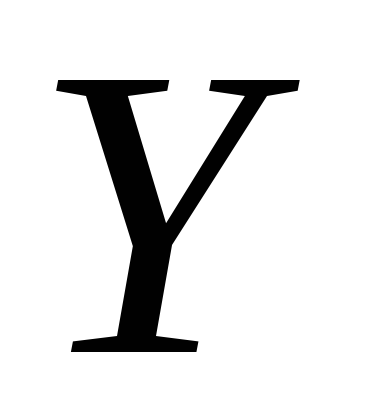 как аксиомы грамматики) регулярную
схему
как аксиомы грамматики) регулярную
схему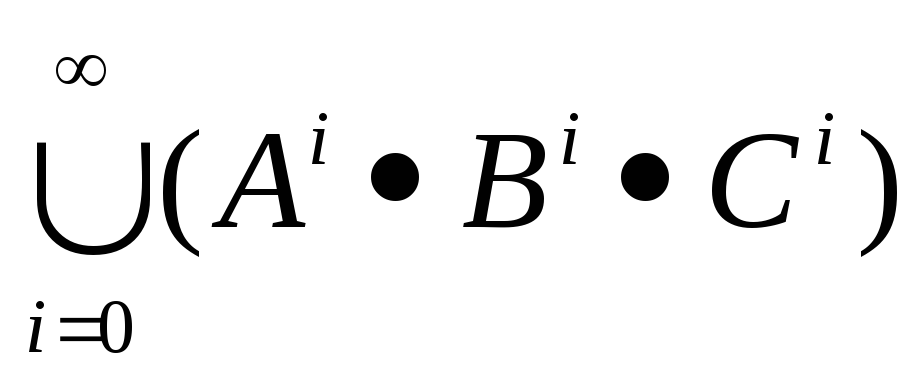 ,
которой в традиционной теории формальных
языков (рассматривая терминальные
сорта элементов как буквы терминального
алфавита, а операцию последовательной
композиции как конкатенацию) соответствует
язык, не являющийся даже контекстно-свободным.
Построение отдельных сетей этого языка
иллюстрирует рис. 2.5, приведенный выше
как пример выполнения операции
последовательной композиции.
,
которой в традиционной теории формальных
языков (рассматривая терминальные
сорта элементов как буквы терминального
алфавита, а операцию последовательной
композиции как конкатенацию) соответствует
язык, не являющийся даже контекстно-свободным.
Построение отдельных сетей этого языка
иллюстрирует рис. 2.5, приведенный выше
как пример выполнения операции
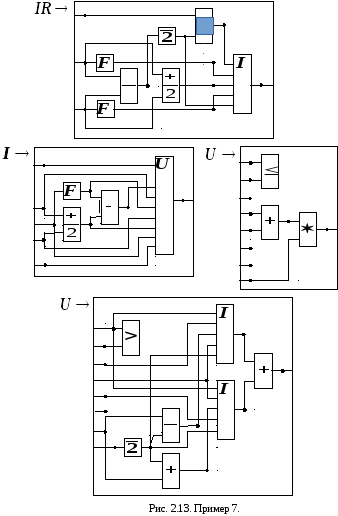
последовательной композиции.Еще один пример приведен на рис. 2.13. Интерпретация
 терминальных сортов элементов такова
(носитель – множество вещественных
чисел):
терминальных сортов элементов такова
(носитель – множество вещественных
чисел): ¤
¤ ¥
¥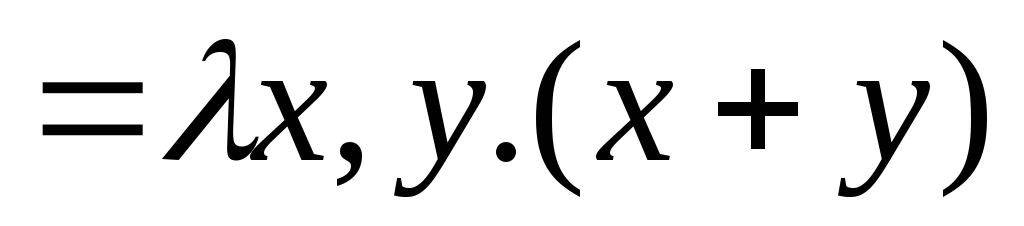 ,
, ¤
¤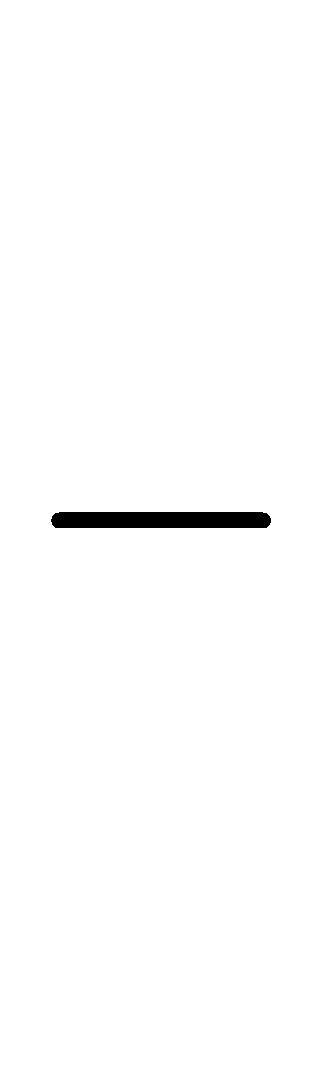 ¥
¥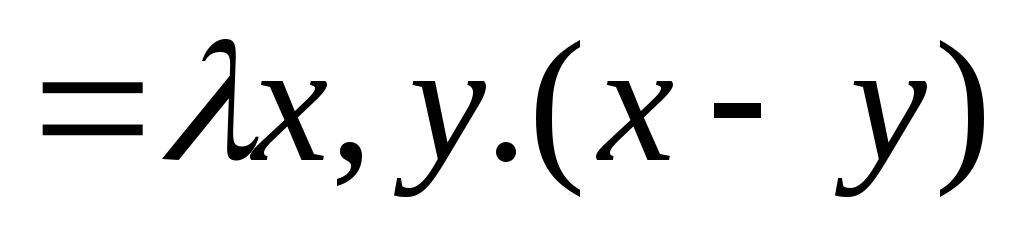 ,
, ¤
¤ ¥
¥ ,
, ¤
¤ ¥
¥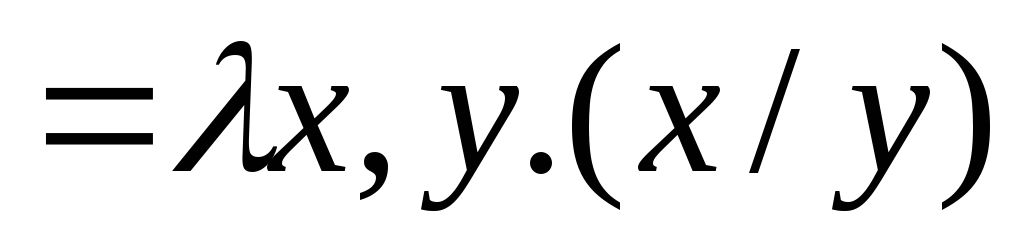 ,
, ¤
¤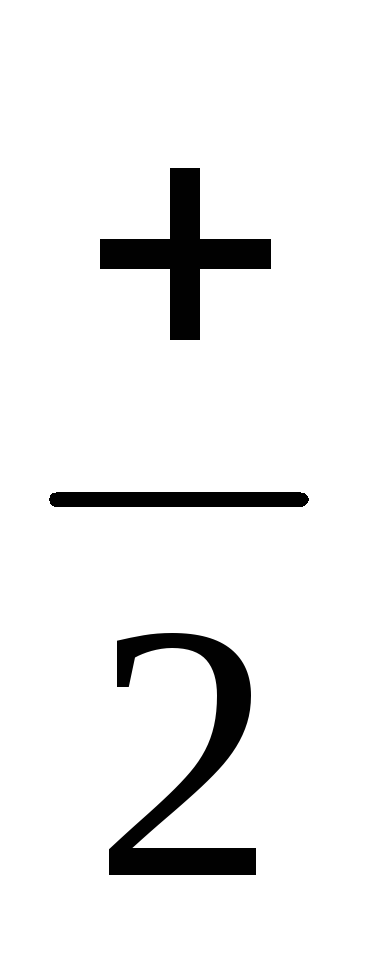 ¥
¥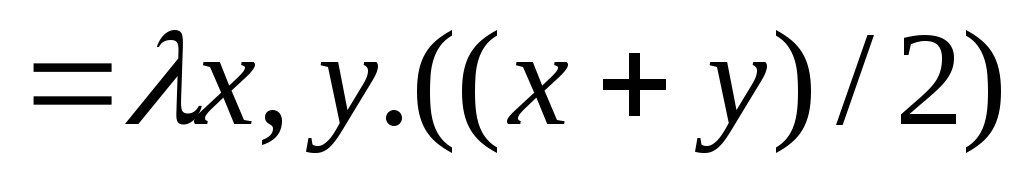 ,
, ¤
¤ ¥
¥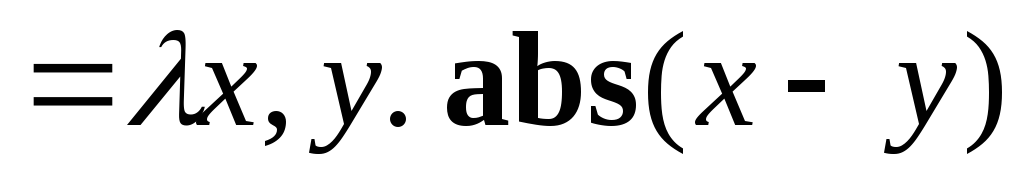 ,
, ¤
¤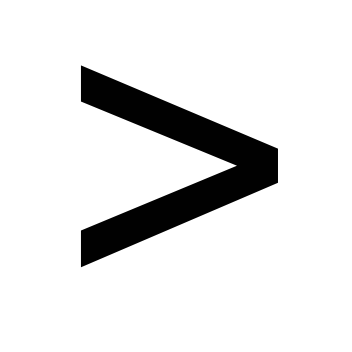 ¥
¥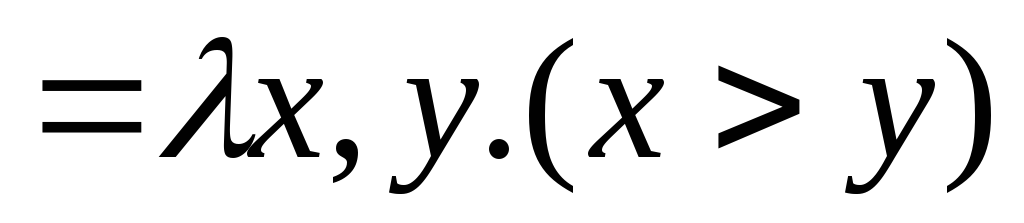 ,
, ¤
¤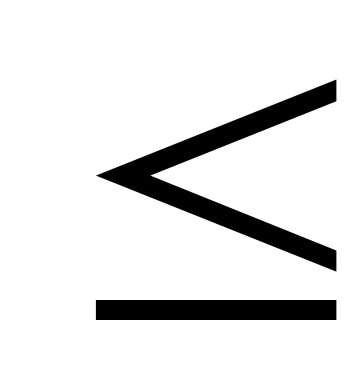 ¥
¥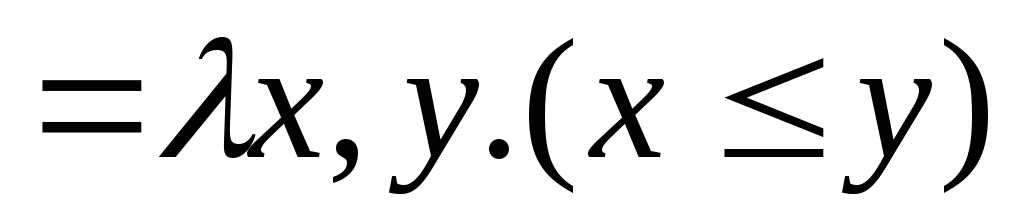 ,
, ¤
¤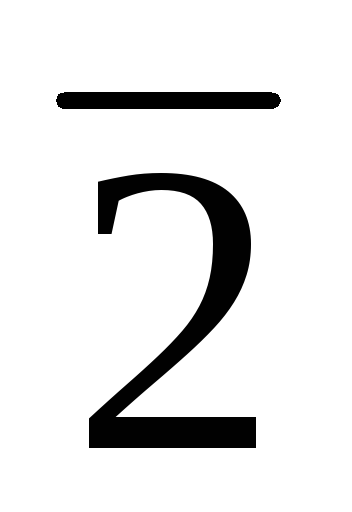 ¥
¥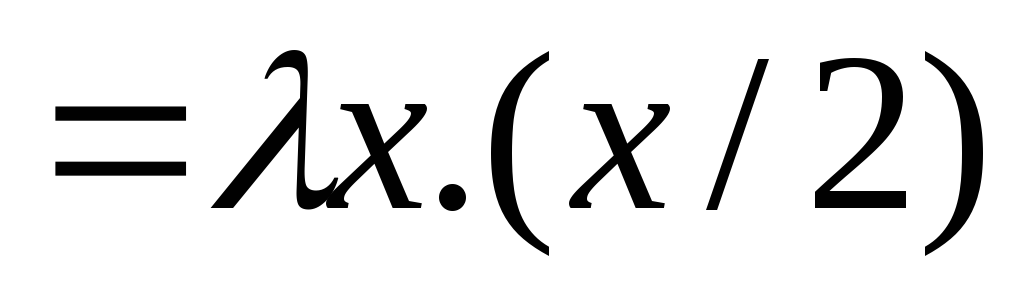 .
Нетерминальный сорт
.
Нетерминальный сорт в этом случае интерпретируется как
функция с параметрами
в этом случае интерпретируется как
функция с параметрами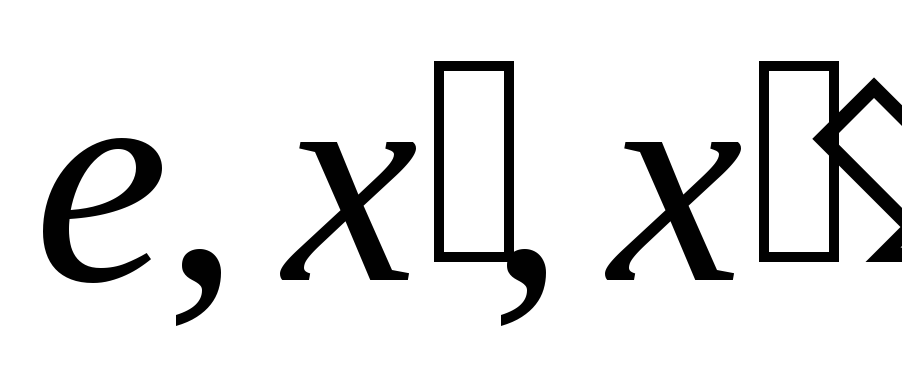 ,
,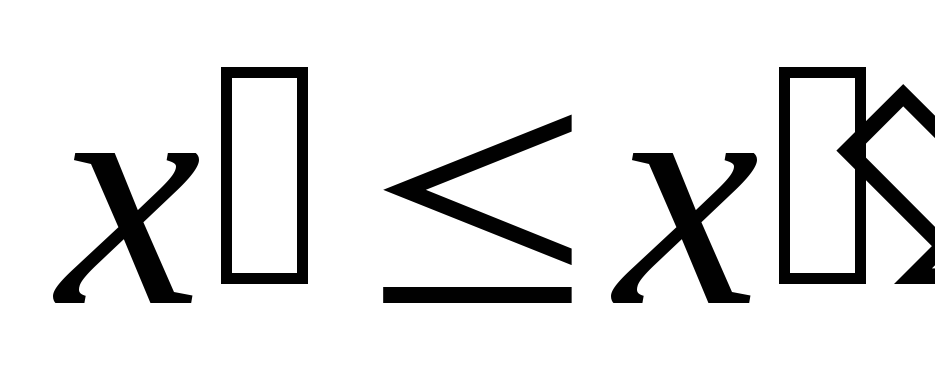 ,
вычисляющая значение определенного
интеграла
,
вычисляющая значение определенного
интеграла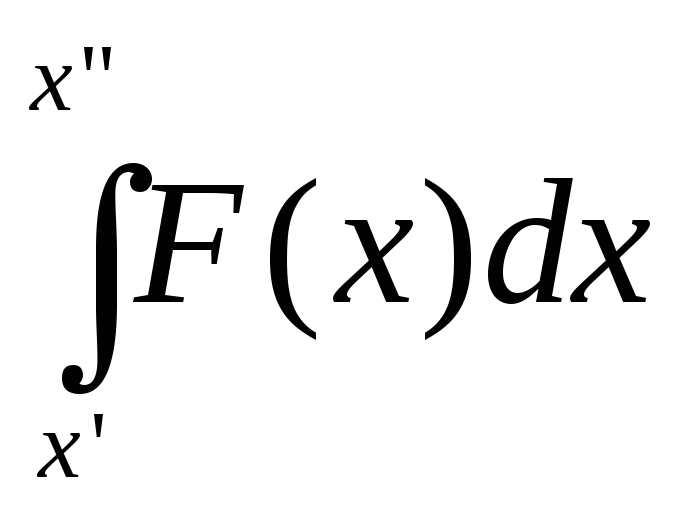 с точностью
с точностью .
Подынтегральная функция представлена
нетерминальным сортом
.
Подынтегральная функция представлена
нетерминальным сортом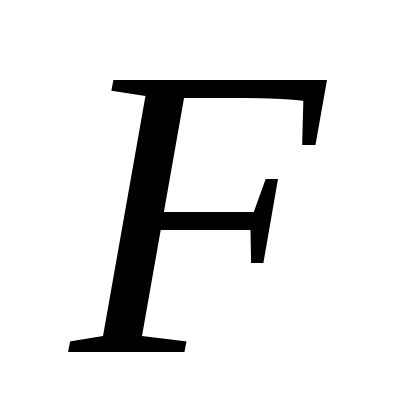 ,
для которого предполагается наличие
определяющих эту функцию правил.
Интеграл вычисляется рекурсивно,
методом трапеций с переменным шагом.
Фактически, носитель в этом примере –
множество кодов-представлений чисел
в доступном формате вещественных чисел,
а интерпретация терминальных символов
– реализация соответствующих функций
и предикатов с доступной точностью над
представлениями чисел в этом формате.
,
для которого предполагается наличие
определяющих эту функцию правил.
Интеграл вычисляется рекурсивно,
методом трапеций с переменным шагом.
Фактически, носитель в этом примере –
множество кодов-представлений чисел
в доступном формате вещественных чисел,
а интерпретация терминальных символов
– реализация соответствующих функций
и предикатов с доступной точностью над
представлениями чисел в этом формате.
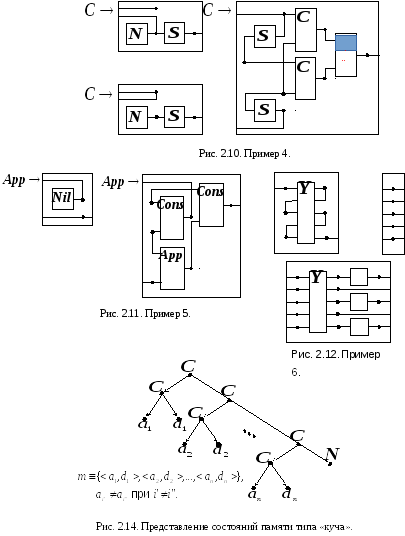
В этом примере рассматриваются операции доступа к памяти типа «куча» (память типа «куча» является одним из основных компонентов архитектуры
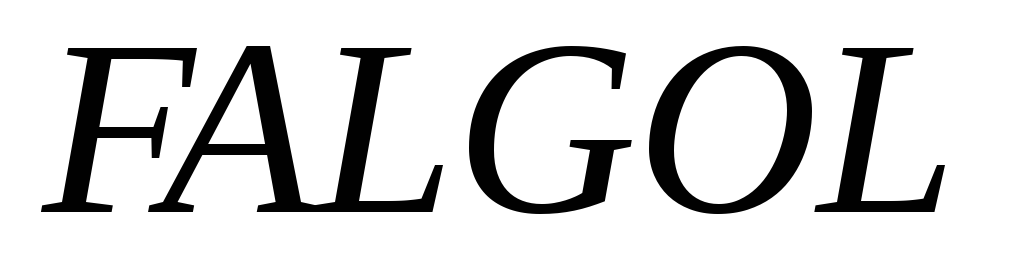 -машины,
описанной в[
].
Пусть нетерминальный сорт
-машины,
описанной в[
].
Пусть нетерминальный сорт
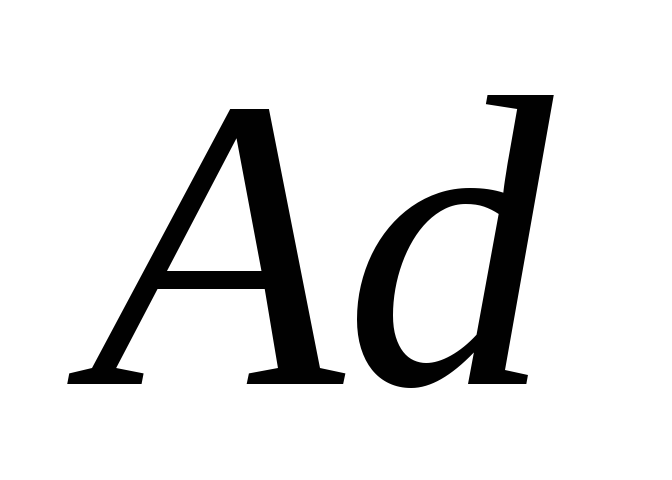 представляет конструктивное счетное
множество «адресов»,
представляет конструктивное счетное
множество «адресов»,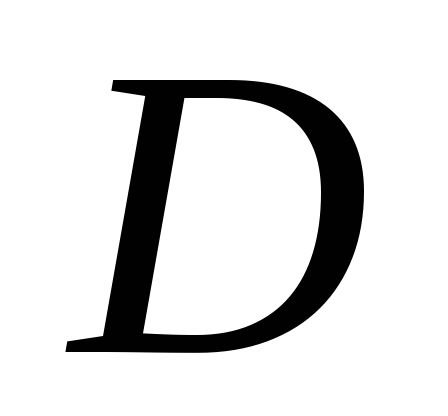 обозначает множество «данных», которые
могут храниться в памяти, а
обозначает множество «данных», которые
могут храниться в памяти, а – множество возможных «состояний»
памяти, представленное структурой,
показанной на рис. 2.14, где
– множество возможных «состояний»
памяти, представленное структурой,
показанной на рис. 2.14, где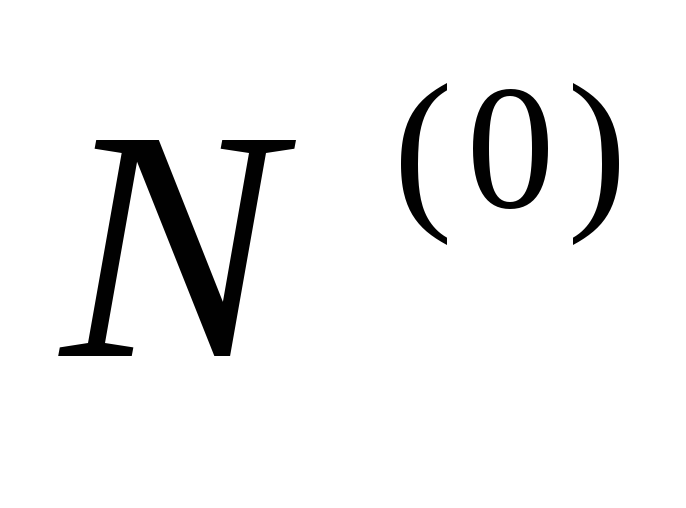 – конструктор «пустой» памяти (с пустым
графиком), а
– конструктор «пустой» памяти (с пустым
графиком), а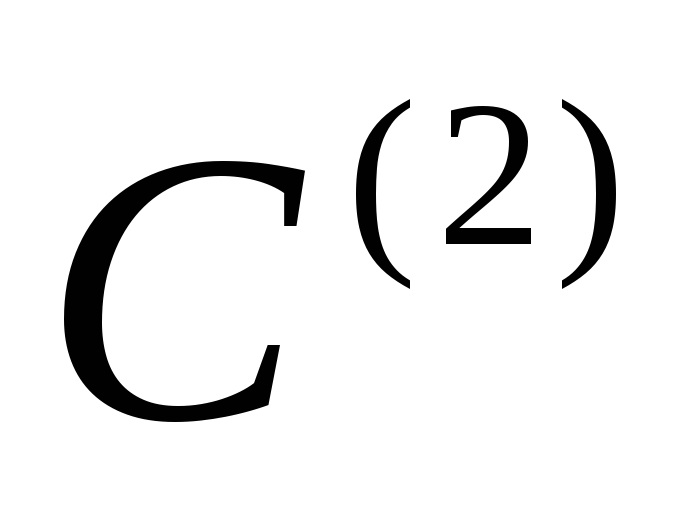 – произвольный бинарный конструктор.
Состояние памяти – множество состояний
«ячеек» памяти с различными адресами.
Состояние ячейки включает адрес ячейки
и «данное», хранящееся в ячейке.
– произвольный бинарный конструктор.
Состояние памяти – множество состояний
«ячеек» памяти с различными адресами.
Состояние ячейки включает адрес ячейки
и «данное», хранящееся в ячейке.
Определим три операции:
функцию адресного чтения:
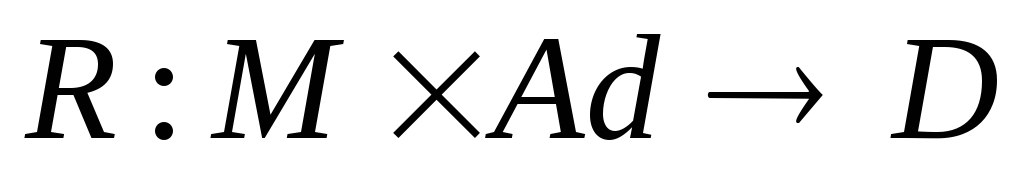 ;
если
;
если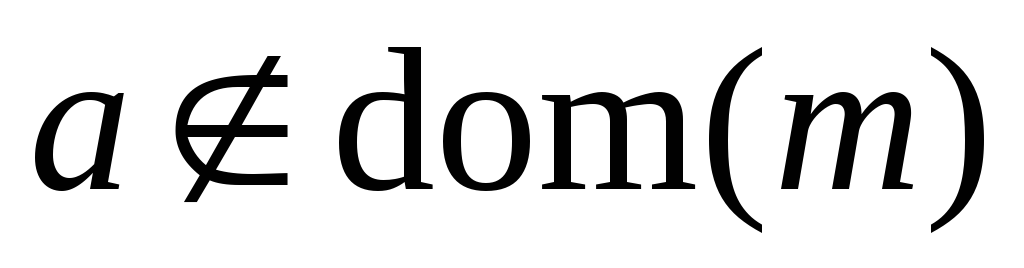 ,
то
,
то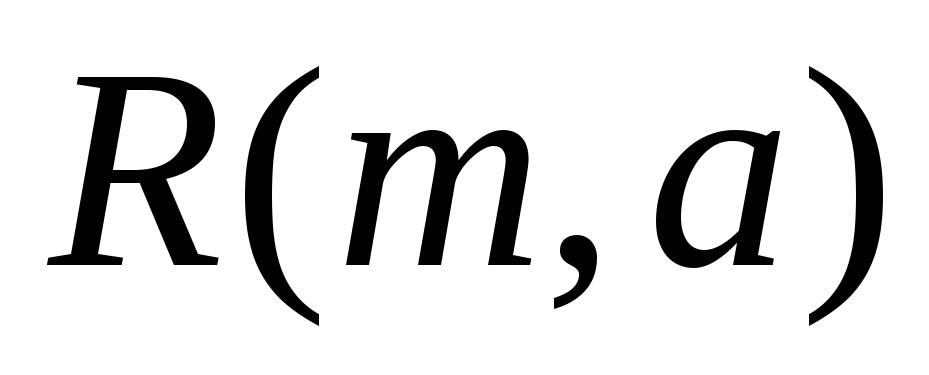 – не определено;
– не определено;функцию адресной записи:
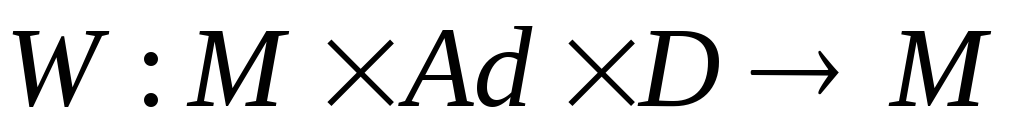 ;
если
;
если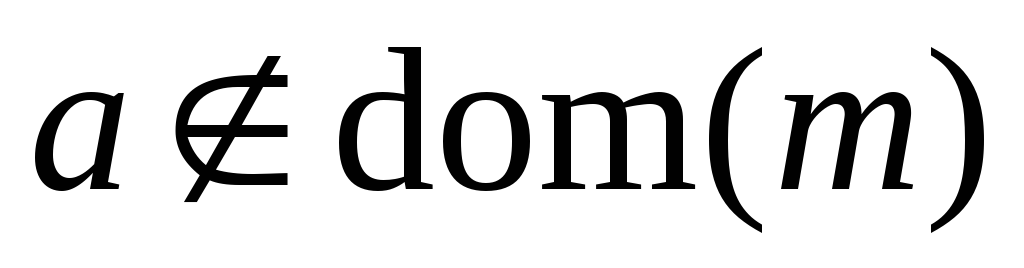 ,
то
,
то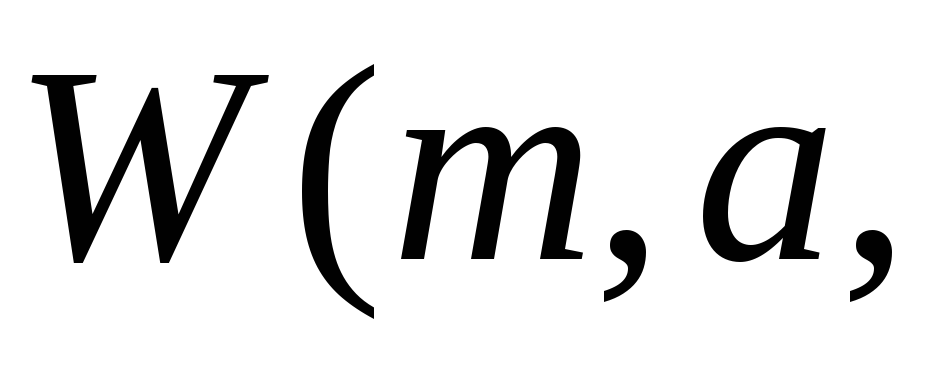
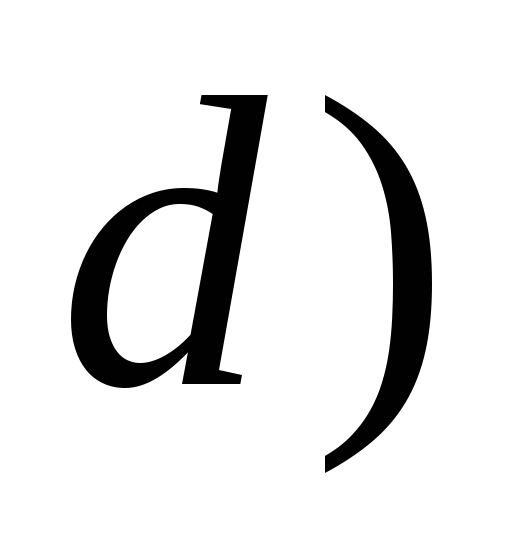 – не определено;
– не определено;отношение (неоднозначное соответствие из
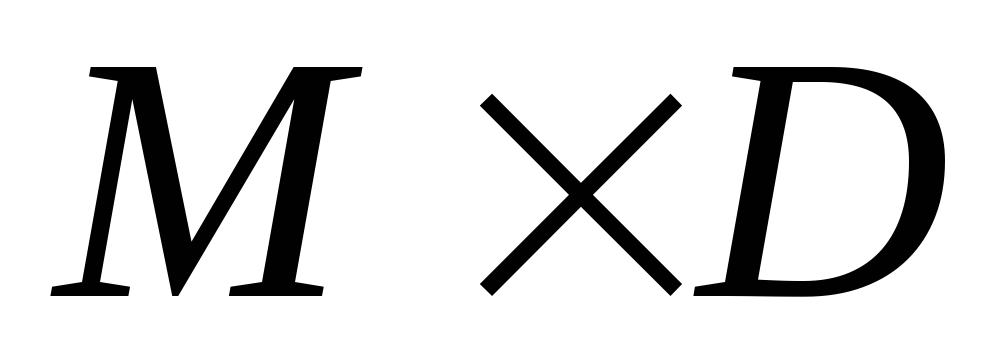 в
в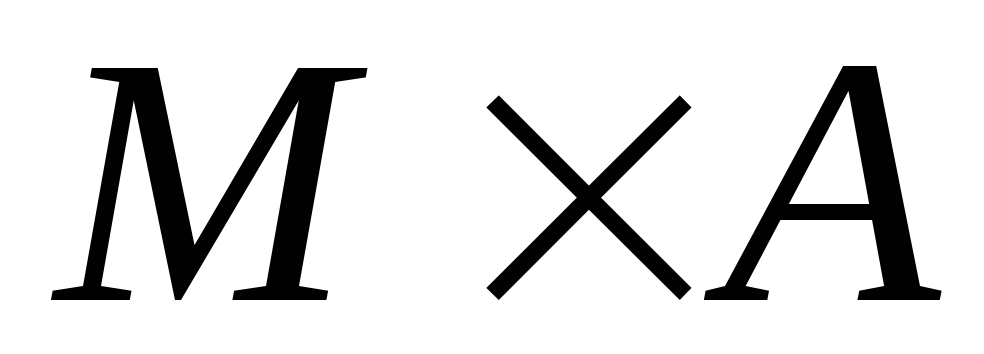 )
инициализации новой ячейки памяти:
)
инициализации новой ячейки памяти:
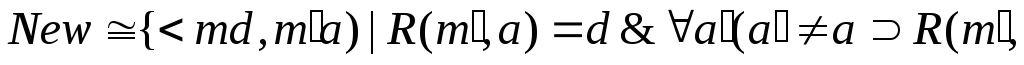
![]() .
.
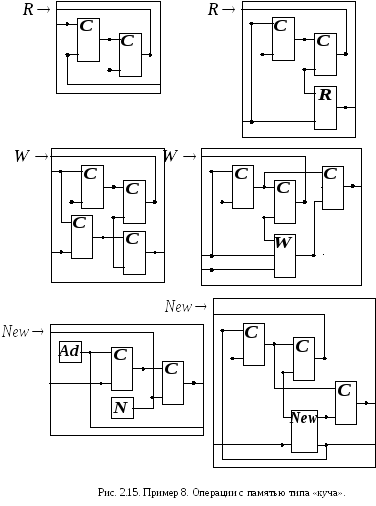
Правила сетевой грамматики, определяющие эти операции, приведены на рис. 2.15.
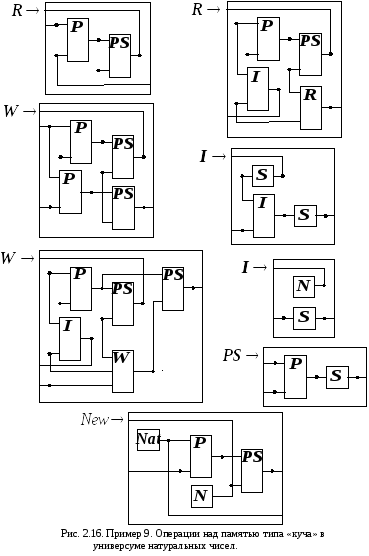
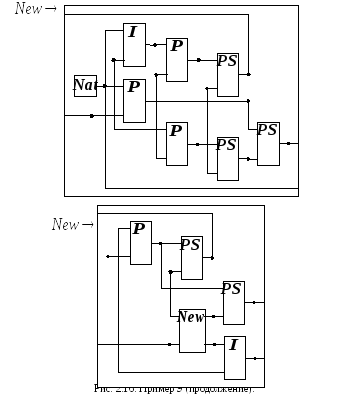
В этом примере (рис. 2.16) рассматривается та же задача, что и в предыдущем. Однако для взаимно-однозначного представления всех объектов – адресов, данных и состояний памяти используются натуральные числа (терминальный базис
 ).
Для представления состояний памяти
используются методы нумерации элементов
конструктивных множеств, в частности,
сведение разнообразия конечных
подмножеств натуральных чисел к
разнообразию кортежей конечной длины
из натуральных чисел. Для построения
номеров различных конструкций будем
использовать суперконструктор
).
Для представления состояний памяти
используются методы нумерации элементов
конструктивных множеств, в частности,
сведение разнообразия конечных
подмножеств натуральных чисел к
разнообразию кортежей конечной длины
из натуральных чисел. Для построения
номеров различных конструкций будем
использовать суперконструктор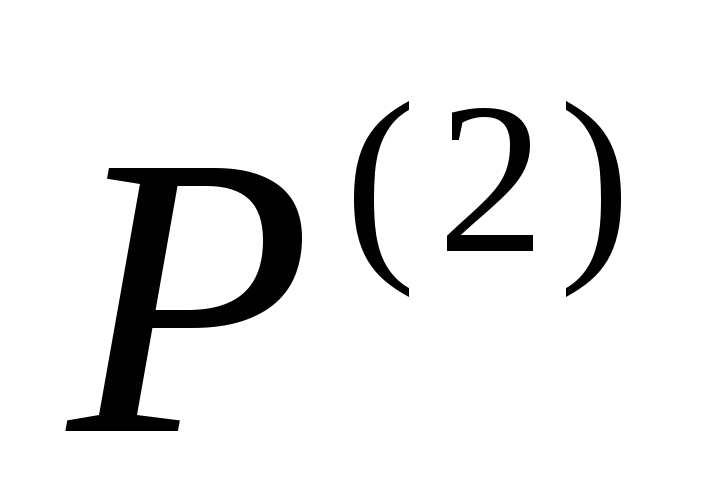 упорядоченной пары на множестве
натуральных чисел, определенный в
примере 3. Помимо операций
упорядоченной пары на множестве
натуральных чисел, определенный в
примере 3. Помимо операций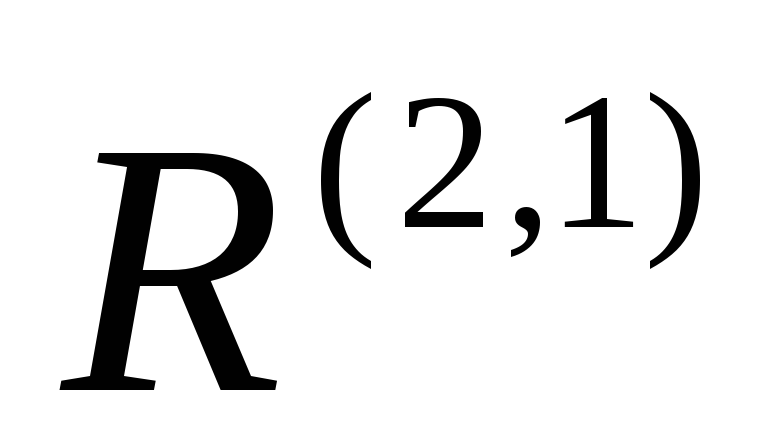 ,
,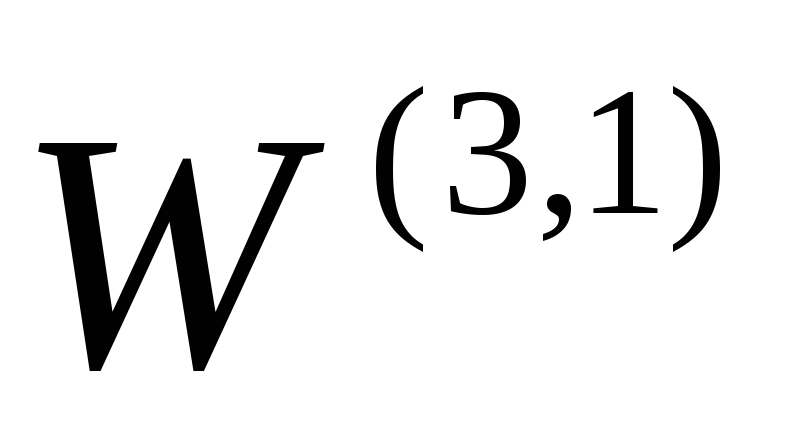 и
и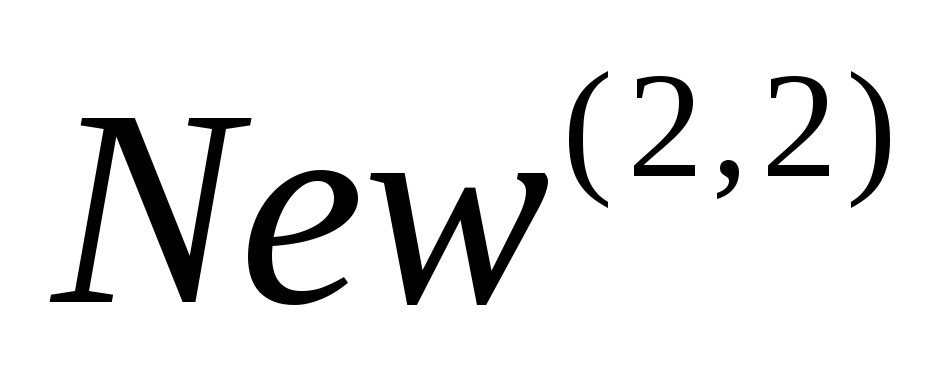 ,
определяется вспомогательная функция
,
определяется вспомогательная функция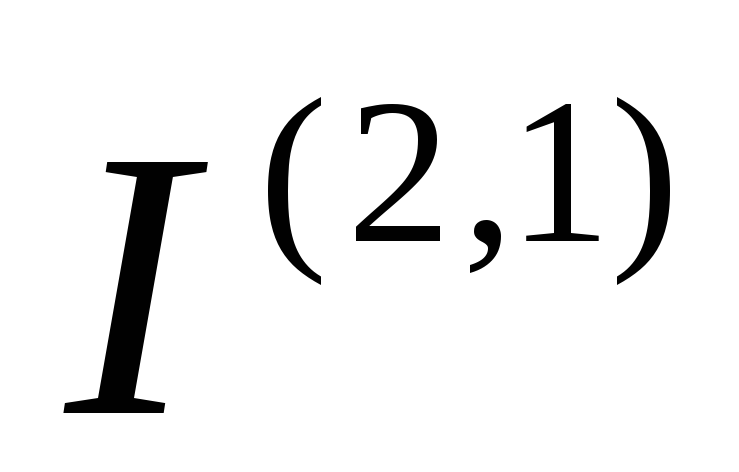 ,
используемая при нумерации конечных
подмножеств натуральных чисел.
,
используемая при нумерации конечных
подмножеств натуральных чисел.