2 . Сетевые языки функционального и логического программирования

2. Сетевые языки функционального и логического программирования

1. Графические представления схем -отношений.

Графические представления различного рода схем, например, схем программ, в теоретическом программировании известны давно. Графическая форма представления функциональных схем была введена еще в [1], а в [2] сетевое представление схем отношений уже играло заметную роль при проведении доказательств и определении моделей вычислений.

Ниже описаны две формы графического представления схем -отношений, помогающие раскрыть сущность базисных операций композиции-отношений и облегчающие решение проблем сильной эквивалентности и включения схем -отношений, введенных в первой главе.

Первое из них, так называемое "лоскутное" () представление (сокращенно,-представление) связано с особенностями базисных операций последовательной и параллельной композиции -отношений и, как нам кажется, поясняет выбор их названий. В -представлении адекватно отражаются как собственные свойства этих операций (см. аксиомы 1,4 ),так и их связь между собой (аксиома 7) и с константами (аксиомы 2,3,5,6).

Рассмотрим простые схемы -отношений, полученные -компози-цией констант и переменных.-Представление таких схем определим индуктивно:

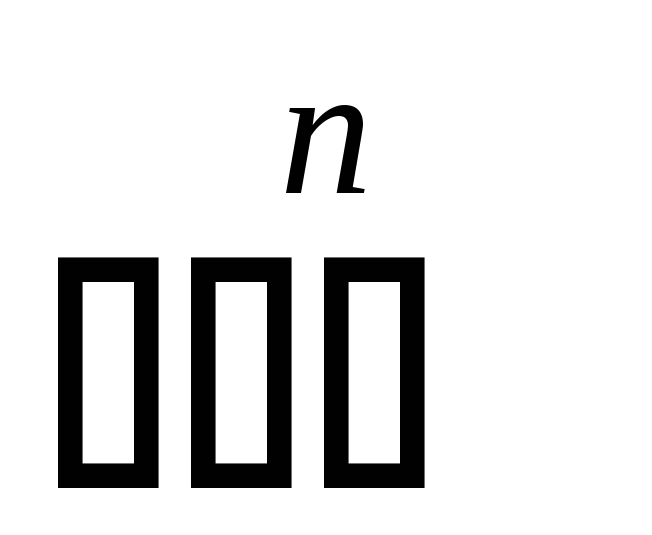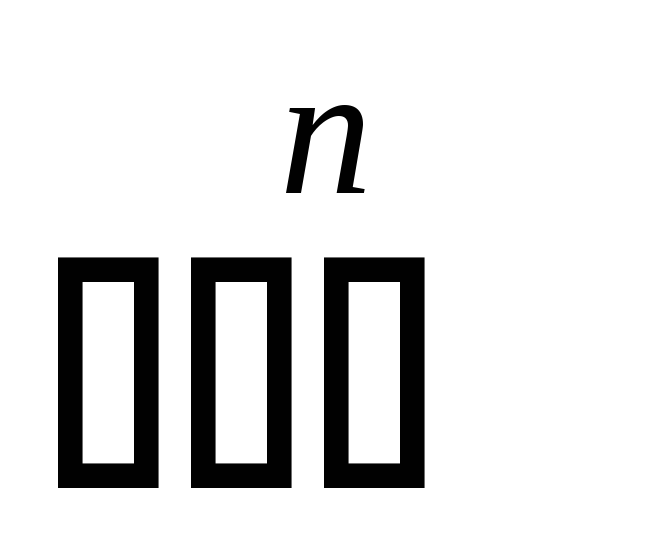
1. элементарные схемы – константы и переменные – изображаются прямоугольниками, внутри которых помещаются соответствующие символы – констант или переменных; для всех случаев, кроме констант , -представления элементарных схем имеют произвольные ненулевые значения размеров представляющих их прямоугольников; для констант  длина, а при 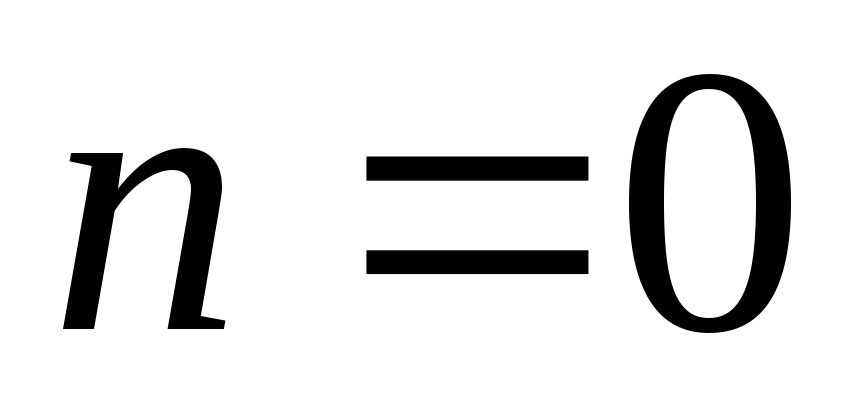и высота могут быть равны нулю, более того, всякий раз, когда это возможно, будем выбирать для них именно нулевые размеры;

2. если и известны-представления схем ис внешними границами в форме прямоугольников, то путем соответствующей трансформации (сжимания или растягивания) в вертикальном направлении они приводятся к одинаковой, в общем случае ненулевой высоте (исключение составляет случай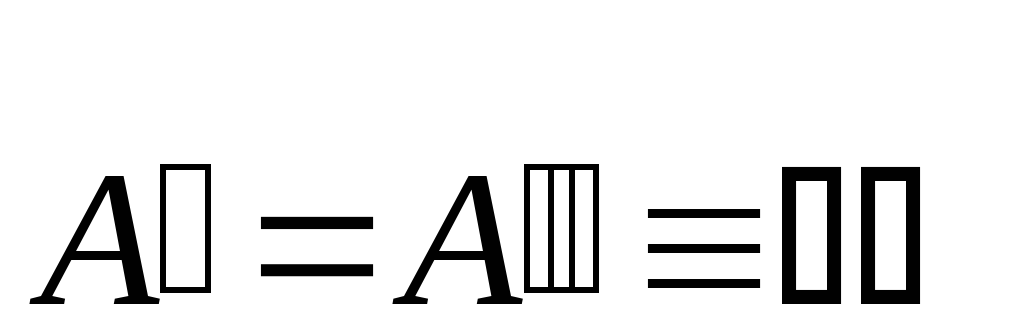), после чего правая граница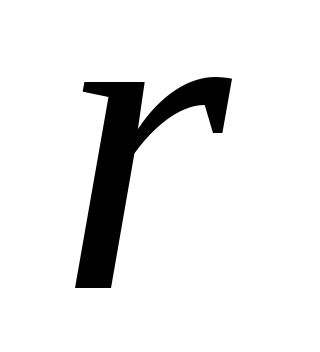-представления 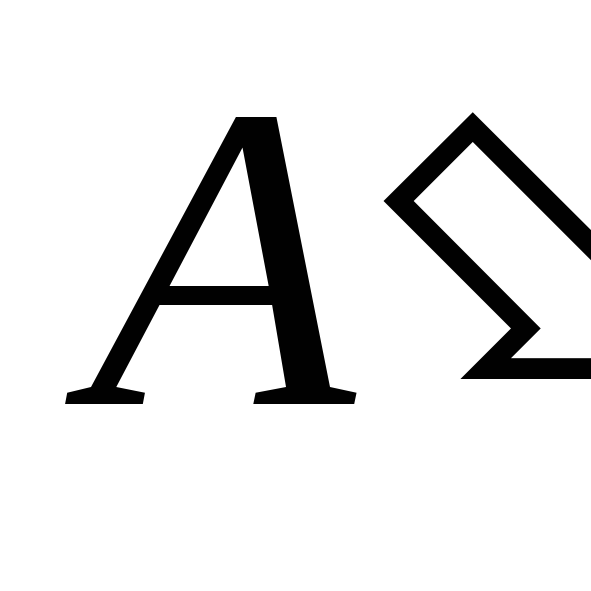совмещается с левой границей-представления (рис. 2.1a);

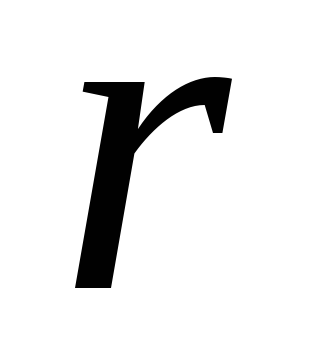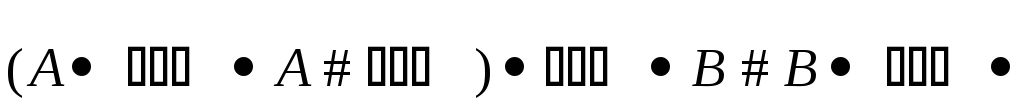
3. если, то путем трансформации-представлений ив горизонтальном направлении они приводятся к одинаковой, в общем случае, ненулевой (кроме случая) длине, после чего нижняя граница-представления совмещается с верхней границей-представления(рис. 2.1b).На рис. 2.1c показан пример -представления схемы 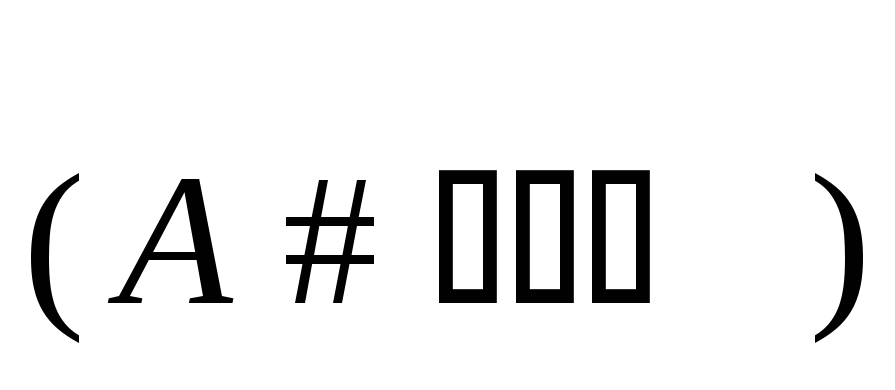, гдеимеет арность, а– арность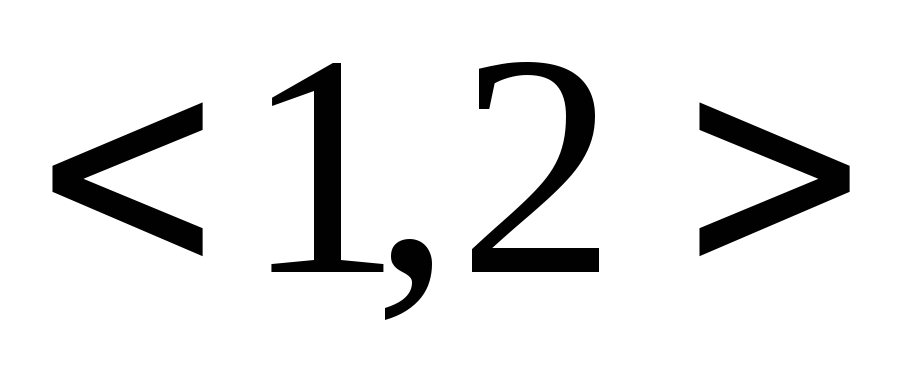. На рис. 2.1d дано графическое пояснение аксиомы 7.

Рис. 2.2 иллюстрирует на примере уже рассмотренной ранее схемы несколько более информативное "лоскутное" представление, отражающее арности всей схемы и отдельных ее подсхем. Такое представление получается в результате отказа от прямоугольной формы -представлений, полагая, что всякая схема арности имеет жесткие только вертикальную левую и вертикальную правую границы, размерамиинекоторых выбранных заранее единиц, соответственно, а соединение попарно их верхних и нижних концов осуществляется идеальными пружинами с ненулевой (а для констант – нулевой) начальной длиной.

Кнеявному использованию-представлений простых схем (например, для доказательства непротиворечивости аксиом 8-15) мы вернемся после того, как введем так называемое сетевое () представление, или, сокращенно, -представление схем -отношений, базирующееся на специальном уточнении понятия сети в некотором базисе элементов и понятия сетевого языка. Последнее понятие является обобщением известного понятия формального языка, для которого в качестве элементов языка выступают не слова в некотором алфавите, а сети в некотором базисе элементов ¹.