Сетевой логический вывод

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

привести к возможности выполнения новых упрощающих преобразований и поэтому может быть использовано при доказательстве нашего утвержде-

ния. При этом важно, что отождествление точек не лишает всю систему свойства нетеровости, т.к. его осуществление хотя и приводит к появле-

нию новой сети в рассматриваемом множестве, но эта сеть является более простой (в ней меньше точек при одинаковых других условиях) по отно-

шению к сети, уже имеющейся в рассматриваемом множестве. Однако разнообразие случаев применения этого преобразования может и должно быть существенно ограничено. Во-первых, чтобы возникла возможность применения преобразования, связанного со свойством функциональности,

отождествляемые точки должны быть одинаковыми по номеру входными точками элементов одного и того же сорта. Во-вторых, т.к. только преоб-

разование, связанное с тотальностью, может привести к уменьшению ко-

личества различных сортов элементов в сети, то достаточно применять отождествление входных точек элементов одного сорта только тогда, ко-

гда эти элементы имеют общую выходную точку. В силу того, что выде-

ленный случай отождествления точек при преобразовании S в S гаран-

тирует эквивалентность S S только тогда, когда связанный с этим пре-

образованием сорт элементов интерпретируется как конструктор (что, со-

гласно определению допустимых интерпретаций логического языка перво-

го порядка, конечно, не является обязательным), то исходная сеть S тоже должна остаться в рассматриваемом множестве сетей.

Наконец, равносильное свойству дополнительности сортов P и P

элементов сетей требование к предикатам, чтобы они, как это предполага-

ется при интерпретации предикатных переменных в логическом языке первого порядка, были всюду определены на D , может быть выражено в форме сетевой эквивалентности так, как показано на рис. 3.2 d . Это огра-

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 21

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

ничение на интерпретацию предикатных символов находит отражение в известной теореме

реализуемой в теории доказательств в форме так называемого правила ре-

золюции (мы приводим здесь только одну из двух двойственных формули-

ровок правила резолюции):

Новый дизъюнктивный член называется резольвентой двух исходных.

Для сетевого представления логических формул в теории направлен-

ных отношений это правило имеет вид, показанный на рис. 3.3. Его спра-

ведливость нетрудно показать следующим образом. Пусть P и P – сорта элементов, интерпретируемые как ортогональные и дополнительные

(k k ) S1P k S1P S ,

т.к. сети в левых частях получены добавлением новых элементов к сетям в правых частях включений. Здесь S1P , S1P – элементарные одноэлементные сети с элементами сортов P и P . Объединяя левые и правые части, по-

лучим

(k k ) S1P (k k ) S1P {S , S }

и далее, используя дистрибутивность объединения относительно операции последовательной композиции, получим

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 22

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

Рис. 3.3. Правило сетевой резолюции.

Отсюда непосредственно следует приведенное выше правило сетевой резолюции.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 23

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

Рис. 3.4. Сети Q и Q .

Это позволяет сделать равносильное для доказательства преобразова-

ние представляющего рассматриваемую логическую формулу множества

цируема к пустой сети, то в качестве правил для аксиомы грамматики

видно, что порождаемый ею язык эквивалентен в интерпретации исходно-

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 24

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

му множеству сетей {S1 , S2 ,...}: по построению грамматики он, с одной стороны, включает все Si , а, с другой стороны, все порождаемые подста-

новками сети (фактически, резольвенты) не расширяют интерпретацию.

Рассмотрим вариант базового языка исчисления предикатов первого порядка (без равенства), т.е. случай, когда среди квазиэлементарных фор-

мул нет формул вида z z .

Для всякой сети в терминальном (теперь чисто функциональном) ба-

зисе можно утверждать, что либо она трансформируется (редуцируется) к

нормальной форме рассмотренными выше преобразованиями, либо будет доказано, что она имеет пустую интерпретацию при любой интерпретации элементов терминального базиса. Можно показать, что

1)интерпретация любого конечного множества непустых сетей в нор-

мальной форме пуста для некоторой удовлетворяющей необходимым требованиям интерпретации элементов базиса и

2)это же свойство сохраняется и для любого рекурсивно-перечислимого множества сетей в нормальной форме, не содержащего пустую сеть

. Следовательно, доказываемое утверждение истинно тогда и только тогда, когда в порождаемый язык входит сеть, редуцируемая к пустой сети , также являющейся сетью в нормальной форме. Таким обра-

зом, проблема является полуразрешимой – множество сетей, порождае-

мых сетевой КС-грамматикой, рекурсивно-перечислимо, а система

правил редукции имеет свойство нетеровости, т.е. любая сеть приводи-

ма к нормальной форме за конечное число шагов.

Т е о р е м а 3 . 6 . Если исходное множество сетей реляционно эквива-

лентно (в сильном смысле) сети , то сеть будет получена в резуль-

тате редукции одной из сетей языка, порожденного описанной выше сете-

вой КС-грамматикой.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 25

3.СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

Вкачестве основы процедуры доказательства можно взять любую корректную процедуру порождения языка по сетевой КС-грамматике. Ес-

ли это – процедура дедуктивного вида, то, исходя из особенностей задачи,

имеется немало возможностей существенного сокращения числа вариантов вывода сетей из аксиомы грамматики. Рассмотрим некоторые из этих си-

туаций.

1. Если в сети (здесь и далее, возможно, содержащей нетерминальные элементы) обнаружен фрагмент (подсеть) вида рис. 3.2 c , то такая сеть ис-

ключается из множества выводимых из аксиомы сетей.

Описываемые далее ситуации 2 и 3 справедливы только для чистого языка исчисления предикатов первого порядка без равенства – в этом слу-

чае среди квазиэлементарных формул в оконечном представлении рас-

сматриваемой формулы не будет неравенств вида z z и, следовательно,

при доказательстве не выполняется каким-то особым образом резолюция по равенству.

2. Если в сети имеется цикл (из элементов терминальных сортов, т.к.

нетерминальные сорта имеют арность m,0 и, таким образом, не могут входить в циклы), то цикл не может быть устранен в любой порожденной сети в процессе рекурсивного вывода из аксиомы и при дальнейшей ре-

дукции. Сеть с циклом, следовательно, не может привести к порождению пустой сети и без ущерба для целей нашего доказательства может быть исключена из процесса вывода. Циклом мы называем фрагмент сети

Рис. 3.5. Цикл в сети.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 26

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

вида, показанного на рис.3.5.

3. Если в сети имеется точка, являющаяся одновременно выходной

точкой двух элементов различных терминальных сортов, то эта ситуация

сохраняется во всех порождаемых из этой сети сетях и, следовательно, то-

же не может привести к порождению пустой сети и подлежит исклю-

чению из процесса вывода.

4. Наиболее сложной в реализации является проверка для каждой но-

денных сетей S , хотя, если это будет установлено (это отношение между

сетями предполагает включение интерпретаций при любой интерпретации элементов базиса), то S может не включаться в число выводимых из ак-

сиомы сетей. Проблема состоит в том, что эта проверка может оказаться более трудоемкой, нежели избыточное продолжение вывода и для S .

3.8.Пример.

Описанная выше схема доказательства методом сетевой резолюции иллюстрируется на примере, логическая формулировка которого позаимствована из книги [Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем // Москва. Наука. 1983].

1) Исходная формула включает три аксиомы и утверждение:

x(E(x) & V (x) y(S(x, y) & C( y))) &x(P(x) & E(x) & y(S(x, y) P( y))) &x(P(x) V (x))

x(P(x) & C(x))

2) элиминируя импликацию, получим

x( E(x) V (x) y(S(x, y) & C( y)))x(P(x) & E(x) & y( S (x, y) P( y)))

x( P(x) V (x))

x(P(x) & C(x))

3) опускаем отрицание до уровня элементарных формул

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 27

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

x(E(x) & V (x) & y( S (x, y) C( y)))x( P(x) E(x) y(S (x, y) & P( y)))

x(P(x) &V (x))

x(P(x) & C(x))

4) для отдельных дизъюнктов строим пренексную нормальную форму

x y(E(x) & V (x) & ( S(x, y) C( y)))x y( P(x) E(x) S(x, y) & P( y))

x(P(x) &V (x))

x(P(x) & C(x))

5) проводя скулемизацию дизъюнктивных членов, получим

Y x(E(x) & V (x) & ( S(x,Y (x)) C(Y (x))))X y( P( X ) E( X ) S( X , y) & P( y))

x(P(x) &V (x))

x(P(x) & C(x))

6)приводя матрицы дизъюнктивных членов к ДНФ, внося кванторы суще-

ствования под знак дизъюнкции и удаляя лишние из них, окончательно сформулируем доказываемое утверждение:

E V S C P Y X

( x(E(x) & V (x) & S (x,Y (x)))

x(E(x) & V (x) & C(Y (x)))

P( X )E( X )

y (S ( X , y) & P( y)))

x (P(x) & V (x))

x (P(x) & C(x)).

На рис. 3.6 показаны сети – результаты трансляции дизъюнктов полу-

ченной формулы. Построим сетевую грамматику с множеством нетерми-

нальных символов {E,V , S,C, P, E ,V , S ,C , P, a}, множеством терминальных символов {Y , X} и аксиомой a . Вид правил для аксиомы показан на

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 28

3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

рис. 3.7 (для всех Q {E,V , S,C, P}), а все остальные правила – на рис. 3.8.

Последовательность подстановок и применений правил редукции, приво-

дящая к построению пустой сети, приведена на рис. 3.9. Следовательно,

рассматриваемая формула является общезначимой.

Рис. 3.8. Пример. Правила грамматики.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 29

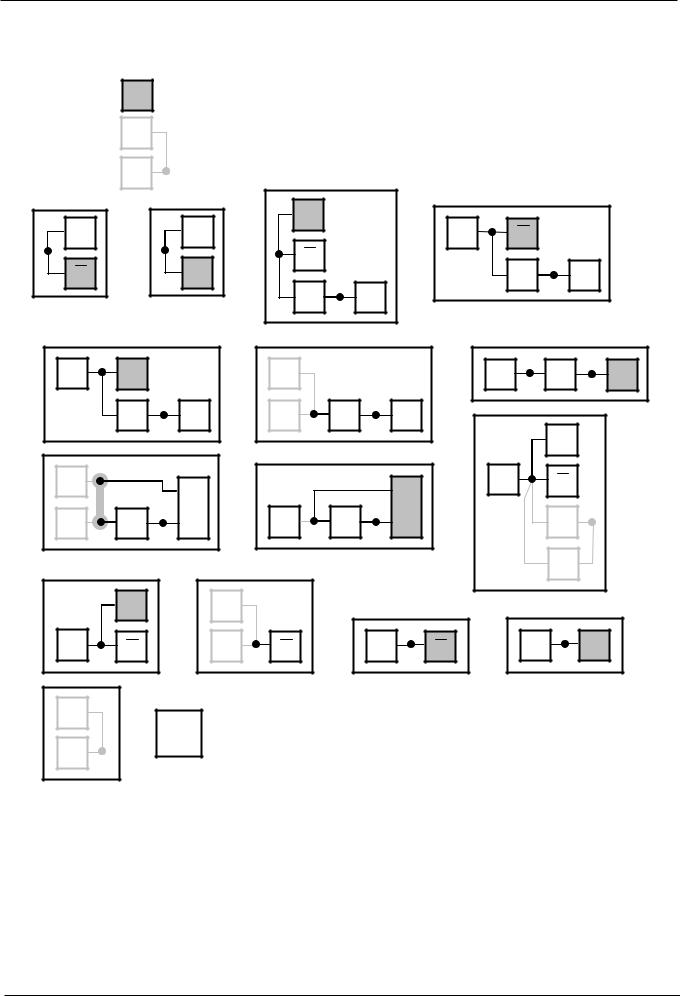
3. СЕТЕВОЙ ЛОГИЧЕСКИЙ ВЫВОД

-элемент, вместо которого выполняется подстановка

-компоненты сети – редексы (вида левых частей правил редукции).

Рис. 3.9. Пример. Процесс вывода

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 30