16

Методические указания к решению задач

Найти сумму ряда , где - целые числа.

Суммой ряда  называется предел последовательности его частичных сумм , т.е. , где .

1. По условию задачи

Если корни знаменателя отличаются на целое число, т.е. , где  – натуральное число, то члены последовательности частичных сумм ряда  легко найти, т.к. в выражении  многие слагаемые взаимно уничтожаются.

2. Раскладываем общий член ряда на элементарные дроби:

.

3. Находим -ю частичную сумму ряда: ,сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле .

Замечание 1. Если коэффициент при  не равен единице, но равен квадрату целого числа, то все выполняется аналогично.

Замечание 2. Если суммирование ряда начинается не с 1, а с некоторого номера , то -я частичная сумма ряда будет .

Примеры решения задач:

1. Найти сумму ряда

Сумма ряда:

где  – сумма  первых членов ряда.

Представим ряд в виде: . Тогда

Сумма ряда

II. Найти сумму ряда , где  – целые числа.

Суммой ряда  называется предел последовательности его частичных сумм , т.е. ,

где .

1. По условию задачи .

Т.к. корни знаменателя отличаются на целое число, то члены последовательности частичных сумм ряда  легко найти, т.к. в выражении  многие слагаемые взаимно уничтожаются.

2. Раскладываем общий член ряда на элементарные дроби: ,

где числа  находим методом неопределенных коэффициентов. Для этого приводим к общему знаменателю дроби в левой и правой части тождества и приравниваем коэффициенты при одинаковых степенях   в числителях слева и справа. В результате получим систему трех уравнений с тремя неизвестными, которая имеет единственное решение.

3. Находим -ю частичную сумму ряда: ,сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле .

2. Найти сумму ряда

Представим общий член ряда в виде

.

Тогда , или

.

Составим систему или или

Тогда

Тогда .

Сумма  первых членов ряда

Сумма ряда .

I признак сравнения

Исследовать сходимость ряда с неотрицательными членами ,

Где  и , … – функции с известными наименьшими и наибольшими значениями, причем функция   монотонно зависит от , …

1. Проверяем, что . (Если , то ряд расходится, т.к. не выполнено необходимое условие сходимости ряда).

2. Поскольку , то можно применить первую теорему сравнения:

Пусть даны два ряда с неотрицательными членами  и .

Если , то из сходимости ряда  следует сходимость ряда .

Если , то из расходимости ряда  следует расходимость ряда .

3. Чтобы сделать вывод о сходимости (расходимости) данного ряда, необходимо установить справедливость одной из двух гипотез:

1) Исходный ряд  сходится.

2) Исходный ряд  расходится.

3.1. Проверяем первую гипотезу. Чтобы установить, что исходный ряд  сходится, нужно найти сходящийся ряд  такой, что .

В качестве эталонного ряда используем одни из следующих рядов:

а) сходящийся гармонический ряд  при  ( – константа);

б) сходящийся геометрический ряд  при  ( – константа).

Если существует сходящийся ряд  такой, что выполняется неравенство , то по первой теореме сравнения исходный ряд  сходится. В противном случае проверяем вторую гипотезу.

3.2. Проверяем вторую гипотезу. Чтобы установить, что исходный ряд  расходится, нужно найти расходящийся ряд  такой, что .

В качестве эталонного ряда  используем одни из следующих рядов:

а) расходящийся гармонический ряд  при  ( – константа);

б) расходящийся геометрический ряд  при  ( – константа).

Если существует расходящийся ряд  такой, что выполняется неравенство , то по первой теореме сравнения исходный ряд  расходится.

Замечание. Для оценки общего члена ряда используем неравенства: , ,

, , .

Примеры решения задач:

1. Исследовать на сходимость ряд .

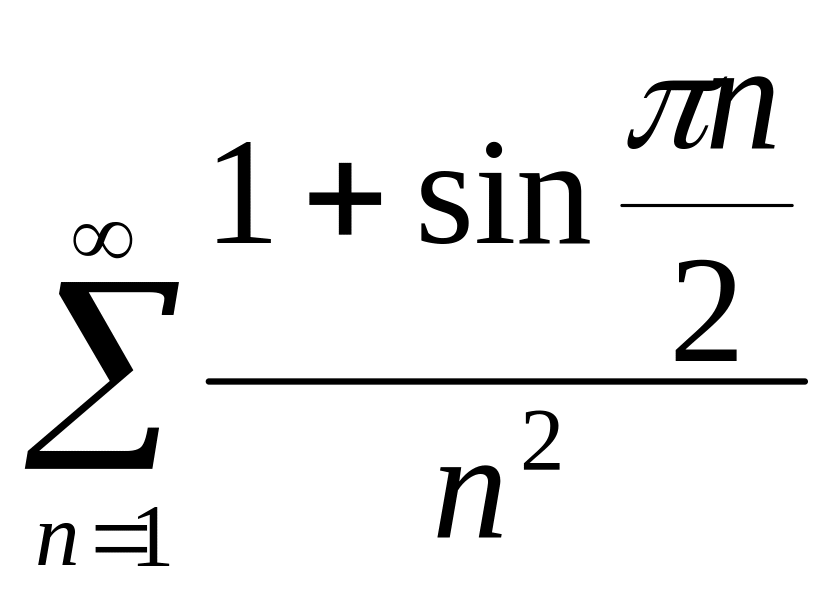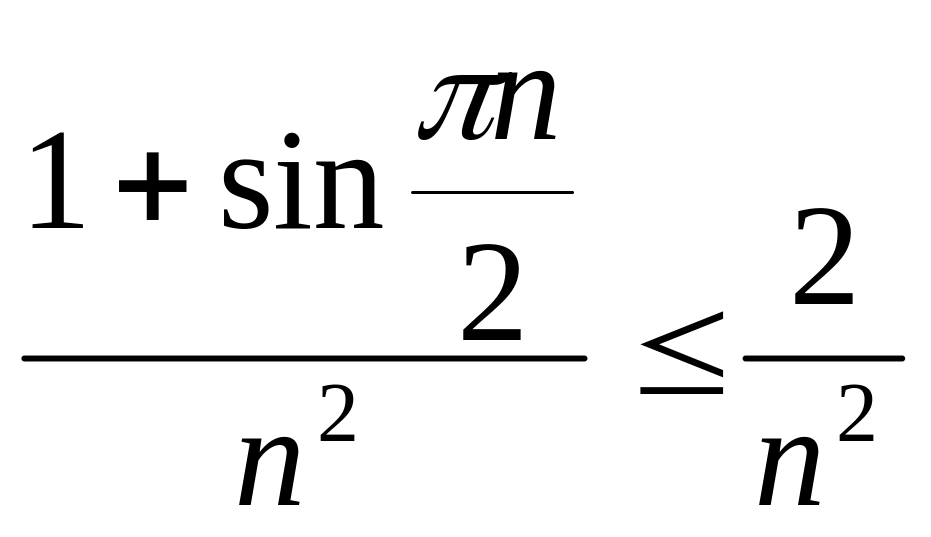Сравним данный ряд с рядом . Т.к. для любых значений  выполняется неравенство , то из сходимости ряда  будет следовать сходимость исследуемого ряда. Ряд  сходится согласно интегральному признаку Коши: .

Значит, сходится и исследуемый ряд.